妙用对数恒等式解题

广东 龙 宇

对数恒等式是指：a=elna或a=lnea，通过该表达式可以沟通指数与对数的运算，在求解不等式的相关问题时，为构造函数提供了更多的可能性.例如，在证明aea≤blnb型问题时，可考虑如下证明方式：(1)以不等式的左边为准，可得aea≤lnb·elnb，其本质即是对“b”利用对数恒等式进行变形，此时即可构造函数y=xex进行求解；(2)以不等式的右边为准，可得ea·lnea≤b·lnb，其本质即是对“a”利用对数恒等式进行变形，此时即可构造函数y=xlnx进行求解.

一、判断函数的奇偶性

【例1】判断函数f(x)=log2(4x+16x)-3x的奇偶性.

分析：若直接利用定义进行判断，对数运算的过程较为复杂，现考虑利用对数恒等式将表达式变形后再进行判断.

解析：对“3x”部分利用对数恒等式可得3x=log223x，

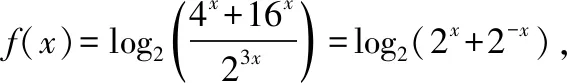
【变式1】判断函数f(x)=loga(a2x+a4x)-3x(a>0且a≠1)的奇偶性.

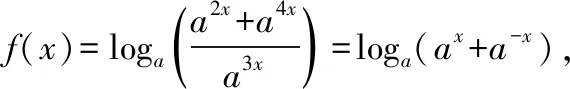
【变式2】判断函数f(x)=loga(a-2x+a-4x)+3x(a>0且a≠1)的奇偶性.

解析：类比上式可得3x=logaa3x，则有f(x)=loga[(a-2x+a-4x)·a3x]=loga(ax+a-x)，从而可得函数f(x)为偶函数.

二、构造函数求最值

(一)试题及求解过程

【例2】已知函数f(x)=alnx+x+1.若不等式xef(x)≤ex对任意的x∈(1,+∞)恒成立，求a的取值范围.

解析：利用对数恒等式可得x-eex=ex-elnx.

将上述函数应用经典不等式：ex≥x+1可得y=ex-elnx≥x-elnx+1.

综上，a的取值范围是(-∞,-e].

(二)试题拓展

解析：利用对数恒等式可得x-mex=ex-mlnx.

将上述函数应用经典不等式：ex≥x+1可得ex-mlnx≥x-mlnx+1.

特别地，当m∈(e,+∞)时，存在两个点使得函数g(x)取到最小值.

拓展方向2：已知函数f(x)=ax-elnx+1.若不等式xef(x)≤ex对任意的x∈(0,+∞)恒成立，求a的取值范围.

根据上述解题经验可得x-eex=ex-elnx≥x-elnx+1.

综上,a的取值范围是(-∞,1].

三、构造函数判断单调性

【例3】(2020·新高考Ⅰ卷(仅供山东使用)·21)已知函数f(x)=aex-1-lnx+lna.

(1)略;(2)若f(x)≥1，求a的取值范围.

分析：原函数具有两个变量，分离的难度非常大，笔者尝试利用对数恒等式将其转化为相同的结构，再构造函数进行求解.

解析：利用对数恒等式可得aex-1=elna+x-1，则有函数f(x)=elna+x-1-lnx+lna.

条件f(x)≥1等价于elna+x-1+lna+x-1≥lnx+x.

对上述不等式右边再次使用对数恒等式可得lnx+x=elnx+lnx.

观察上述不等式构造函数F(x)=x+ex，显然可得函数F(x)在(-∞,+∞)上单调递增.

上述不等式等价于F(lna+x-1)≥F(lnx)，结合单调性可得原不等式等价于lna+x-1≥lnx.

此时即可实现参数分离：即有lna≥lnx-x+1.

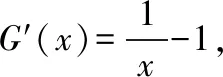
所以a的取值范围为[1,+∞).

【变式】已知函数f(x)=eax-lnx+(a-1)x，若f(x)≥0，求a的取值范围.

解析：条件f(x)≥0等价于eax+ax≥lnx+x.对不等式左边利用对数恒等式变形可得eax+lneax≥lnx+x.

观察上述不等式构造函数F(x)=x+lnx，显然可得函数F(x)在(-∞,+∞)上单调递增.