一个点并路的补图的色等价图类

李丹阳，马海成

青海民族大学 数学与统计学院，西宁 810007

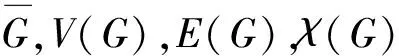
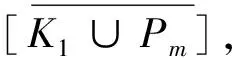
为了找到K1∪Pm(m≥2)的所有伴随等价图，按m+1所含的最大奇因数是1，3，5，9，15或其他奇数分为6种情形．为方便，用δ(G)表示图G的所有不同构的伴随等价图的个数．δ(G)=1当且仅当G是伴随唯一的．为方便读者阅读，下面列出文献[16]中的12个等价桥：

(1)P2m+1～Pm∪Cm+1(m≥3)；

(2)T1，1，n～K1∪Cn+2(n≥2)；

(3)T1，2，n～K1∪Dn+3；

(4)P4～K1∪C3；

(5)K1∪P5～P2∪T1，1，1；

(6)C4～D4；

(7)P2∪C6～P3∪D5；

(8)P2∪C9～P5∪D6；

(9)K1∪C9～T1，1，1∪D6；

(10)P2∪C15～P5∪C5∪D7；

(11)K1∪C15～T1，1，1∪C5∪D7；

(12)C15∪D6～C5∪C9∪D7．

定理1若m+1=2n+1对某个正整数n成立，则

δ(K1∪Pm)=n2+1

证设H～K1∪Pm，H1是H的一个连通分支，使得β(H1)=β(Pm)，H=H1∪H2．

若H1=P7，由K1∪P7～H=P7∪H2得H2～K1，由K1伴随唯一得到H2=K1．

若H1=C4，利用伴随等价桥(1)，H=C4∪H2～K1∪P7～K1∪P3∪C4，从而得到H2～K1∪P3，再由文献[16]中的推论3.2知K1∪P3伴随唯一，所以H2=K1∪P3．

若H1=D4，利用伴随等价桥(1)和(6)，H=D4∪H2～K1∪P7～K1∪P3∪D4，从而得到H2=K1∪P3．

若H1=T1，1，2，利用伴随等价桥(1)和(2)，H=T1，1，2∪H2～K1∪P7～K1∪P3∪C4～P3∪T1，1，2，从而得到H2=P3．故δ(K1∪P7)=4．

假设结论对n-1(n≥3)，即m′+1=2n成立．由文献[16]中的引理2.7 知H1=Pm，Cm2+1，T1，1，m2-1．

若H1=Pm，由K1∪Pm～H=Pm∪H2，得H2=K1．

若H1=Cm2+1，利用伴随等价桥(1)，

H=Cm2+1∪H2～K1∪Pm～K1∪Pm2∪Cm2+1

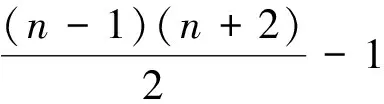
若H1=T1，1，m2-1，利用伴随等价桥(1)和(2)，

H=T1，1，m2-1∪H2～K1∪Pm～T1，1，m2-1∪Pm2

从而得到H2～Pm2．再由文献[17]中的定理1 知这样的H2共有n个．

故

若H1=P11，由H=P11∪H2～K1∪P11得H2=K1．

若H1=C6，利用伴随等价桥(1)，H=C6∪H2～K1∪P11～K1∪P5∪C6，得H2～K1∪P5，又由n=2的情形知H2=K1∪P5，P2∪T1，1，1．

若H1=T1，1，4，利用伴随等价桥(1)和(2)，H=T1，1，4∪H2～K1∪P11～K1∪P5∪C6～P5∪T1，1，4，从而得到H2～P5，由文献[16]中的推论3.2知P5是伴随唯一的，所以H2=P5．

若H1=D5，利用伴随等价桥(1)，(5)和(7)，H=D5∪H2～K1∪P11～K1∪P5∪C6～P2∪T1，1，1∪C6～P3∪D5∪T1，1，1，从而得到H2～P3∪T1，1，1，又由文献[16]中的推论3.2知P3∪T1，1，1是伴随唯一的，所以H2=P3∪T1，1，1．

若H1=T1，2，2，利用伴随等价桥(1)，(3)和(7)，H=T1，2，2∪H2～K1∪D5∪H2～K1∪P11～K1∪P5∪C6～P2∪T1，1，1∪C6～P3∪D5∪T1，1，1，从而得到K1∪H2～P3∪T1，1，1，由于P3∪T1，1，1是伴随唯一的，所以这样的H2是不存在的．故δ(K1∪P11)=5．

假设结论对n-1(n≥3)，即m′+1=3×2n-2成立．由文献[16]中的引理2.7知H1=Pm，Cm2+1，T1，1，m2-1．同类似，我们得到H2～K1，K1∪Pm2，Pm2．由归纳假设和文献[17]中的定理1 知，这样的H2分别有1 个，个或n-2个，故

若H1=P9，由H=P9∪H2～K1∪P9得H2=K1．

H1=C5，利用伴随等价桥(1)，H=C5∪H2～K1∪P9～K1∪P4∪C5，得H2～K1∪P4，又由n=1的情形知H2=K1∪P4，2K1∪C3．

若H1=T1，1，3，利用伴随等价桥(1)和(2)，H=T1，1，3∪H2～K1∪P9～K1∪P4∪C5～P4∪T1，1，3，得H2～P4，又由文献[17]中的定理1得H2=P4，K1∪C3．故δ(K1∪P9)=5．

假设结论对n-1(n≥3)，即m′+1=5×2n-2成立．由文献[16]中的引理2.7 知H1=Pm，Cm2+1，T1，1，m2-1．同类似，我们得到H2～K1，K1∪Pm2，Pm2．由归纳假设和文献[17]中的定理1 知，这样的H2分别有1个，(n-1)2+1个或2(n-1)个，故

δ(K1∪Pm)=1+(n-1)2+1+2(n-1)=n2+1

若H1是前4个图，相应地，H2～K1，K1∪P8，P8，P8∪T1，1，1，由文献[16]中的推论3.2知这些图都是伴随唯一的，所以H2=K1，K1∪P8，P8，P8∪T1，1，1．

若H1=T1，2，3，利用伴随等价桥(1)，(3)和(9)，H=T1，2，3∪H2～K1∪D6∪H2～K1∪P17～K1∪P8∪C9～P8∪T1，1，1∪D6，得K1∪H2～P8∪T1，1，1，又由于P8∪T1，1，1是伴随唯一的，所以这样的H2是不存在的．故δ(K1∪P17)=4．

假设结论对n-1(n≥3)，即m′+1=9×2n-2成立．由文献[16]中的引理2.7知H1=Pm，Cm2+1，T1，1，m2-1．同类似，我们得到H2～K1，K1∪Pm2，Pm2．由归纳假设和文献[17]中的定理1 知，这样的H2分别有1个，个或n-1个，故

若m+1=2n+1对某个正整数n成立，或m+1=2n-1×(2k-1)(k≠2)对某对正整数n，k成立，令

Ω1={Pm1，Pm2∪Cm2+1，Pm3∪Cm2+1∪Cm3+1，…，Pmn∪Cm2+1∪Cm3+1∪…∪Cmn+1}

若m+1=3×2n-1对某个正整数n成立，令

Ω2={Pm1，Pm2∪Cm2+1，Pm3∪Cm2+1∪Cm3+1，…，Pmn-1∪Cm2+1∪Cm3+1∪…∪Cmn-1+1}

若m+1=5×2n-1对某个正整数n成立，令

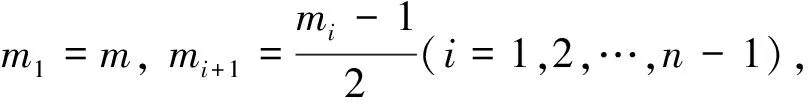
若m+1=2n+1对某个正整数n成立，则

若m+1=3×2n-1对某个正整数n成立，则

若m+1=5×2n-1对某个正整数n成立，则[Pm]=Ω1∪Ω3；

若m+1=2n-1×(2k+1)(k≠1，2)对某对正整数n和k成立，则[Pm]=Ω1．

若m+1=2n+1对某个正整数n成立，或m+1=2n-1×(2k-1)(k≠2)对某对正整数n，k成立，由等价桥(2)我们知道，集合Ω1中的每一个含有圈分支的图中的每一个圈与一个孤立点K1相遇就会等价于一个T-形分支．令

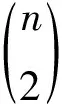
若m+1=2n+1对某个正整数n成立，由等价桥(6)，Θ1中的图K1∪P3∪C4∪C8∪…∪Cm2+1等价于K1∪P3∪D4∪C8∪…∪Cm2+1，再利用等价桥(2)使得图K1∪P3∪D4∪Cm2+1∪…∪Cmn-1+1中的每一个圈分支与一个孤立点K1相遇就会等价于一个T-形分支，令

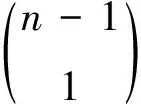
若m+1=3×2n-1，n≥3．由等价桥(2)知集合Ω2中的每一个含有圈分支的图中的每一个圈与一个孤立点K1相遇就会等价于一个T-形分支．令

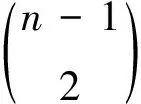
若m+1=5×2n-1，K1∪Pm的等价图除集合Θ1中的图外，还有集合{K1∪H：H∈Ω3}中的图．由等价桥(2)，{K1∪H：H∈Ω3}中的图2K1∪C3∪C5∪…∪Cm2+1中除C3外的任何两个圈与两个孤立点2K1相遇就会等价于两个T-形分支．令

Δ2={C3∪T1，1，3∪T1，1，8∪…∪Cm2+1，C3∪C5…∪T1，1，m3-1∪T1，1，m2-1}

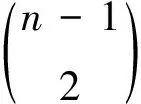
若m+1=9×2n-1，n≥2，K1∪Pm的等价图除集合Θ1中的图外，还包含图P8∪T1，1，1∪D6∪C18∪…∪Cm2+1．由等价桥(9)，集合Θ1中的图K1∪P8∪C9∪…∪Cm2+1等价于图P8∪T1，1，1∪D6∪C18∪…∪Cm2+1．

若m+1=15×2n-1，n≥2，K1∪Pm的等价图除集合Θ1中的图外，还包含图P14∪T1，1，1∪C5∪D7∪C30∪…∪Cm2+1．由等价桥(11)，集合Θ1中的图K1∪P14∪C15∪…∪Cm2+1等价于图P14∪T1，1，1∪C5∪D7∪C30∪…∪Cm2+1．

于是，我们得到下面的结果：

定理2若m+1=2n+1对某个正整数n成立，则

[K1∪Pm]=Θ1∪{K1∪H：H∈Ω3}∪Δ2

证由文献[16]中的等价变换规律，这些图均等价于K1∪Pm，且图的个数也等于δ(K1∪Pm)．