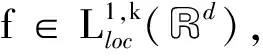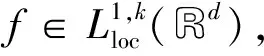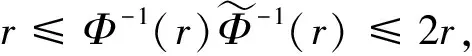基于Dunkl集上分数次极大算子及其交换子在广义Orlicz-Morrey空间上的估计

芮俪，逯光辉

西北师范大学 数学与统计学院，兰州 730070

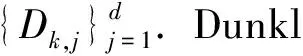
对任意v∈Rd{0}，定义σv为v垂直于超平面Hv⊂Rd的反射

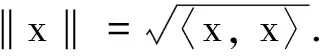
设由反射族{σv}v∈D构成的有限群G为根系统反射群．对任意v∈R，kv≥0，用hk表示Rd上的权函数，有

B(x，r)={y∈Rd：|x-y|

是中心为x∈Rd且半径为r的球，在Dunkl集上的测度为

其中

Sd-1是Rd上的单位球，dσ为标准化曲面测度．

其中

且fB(x，r)表示函数f在球B(x，r)上的平均值．

给定b∈BMOk(Rd)，与带Dunkl集的分数次极大算子相关的交换子Mα，k，b定义为

则称Φ为Young函数．

全文用Y表示满足0<Φ(r)<∞的全体Young函数构成的集合．根据凸性以及Φ(0)=0，容易验证Young函数都是增的．

定义2[16]设Φ∈Y，则带有Dunkl集的Orlicz空间LΦ，k(Rd)定义为

且

带有Dunkl集的弱Orlicz空间WLΦ，k(Rd)的定义为

且

其中

接下来，我们回顾一些逆函数的有关概念[12]．对于一个函数Φ∈Y，且0≤t≤∞，设

Φ-1(t)=inf{r≥0：Φ(r)>t}

类似地，我们给出如下带有Dunkl集的广义Orlicz-Morrey空间的定义：

定义3设φ(x，r)>0为Rd×(0，∞)上的可测函数，Φ∈Y，带有Dunkl集的广义Orlicz-Morrey空间定义为

其中

相应地，带有Dunkl集的弱广义Orlicz-Morrey空间定义为

其中

全文中，C表示与主要参数无关的常数，其值在不同的地方可能不尽相同．对于Rd上的可测子集E，χE表示其上的特征函数．

引理2[16]设Φ∈Y，则对任意球B⊂Rd，有

引理3[16]设Φ∈Y，则对任意球B，有

引理4[16]若f∈BMOk(Rd)，则存在p∈[1，∞)，有

且对任意0<2r

引理5[15]设Φ∈Y∩Δ2，球B⊂Rd，f∈LΦ，k(B)，则对于1

其中C是不依赖于f和b的正常数．

定理1设0<α

(1)

(2)

则Mα，k从MΦ，φ1，k(Rd)到MΨ，φ2，k(Rd)有界．

‖Mα，kf‖LΨ，k(B)≤‖Mα，kf1‖LΨ，k(B)+‖Mα，kf2‖LΨ，k(B)

由Mα，k从LΦ，k(Rd)到LΨ，k(Rd)有界[13]，得到

设任意z∈B，注意到当B(z，t)∩(Rd2B)=∅时，有t>r．事实上，若y∈B(z，t)∩(Rd2B)，有t>|y-z|≥|x-y|-|x-z|>2r-r=r．另一方面，若y∈B(z，t)∩(Rd2B)，有|x-y|≤|y-z|+|x-z|

由引理2、引理3和(1)式，有

则有

结合(2)式可知

定理2设0<α

(3)

(4)

则Mα，k，b从MΦ，φ1，k(Rd)到MΨ，φ2，k(Rd)上有界．

证设0<α

‖Mα，k，bf‖LΨ，k(B)≤‖Mα，k，bf1‖LΨ，k(B)+‖Mα，k，bf2‖LΨ，k(B)

由Mα，k，b从LΦ，k(Rd)到LΨ，k(Rd)有界[13]，得到

对任意的z∈B，B(z，t)∩(Rd2B)=∅，且B(z，t)∩(Rd2B)⊂B(x，2t)．因此

进一步，得到

由引理2、引理1、引理3和引理4，有

对于J2，由引理4、(3)式和引理3，有

由J1，J2的估计可得

则可得到

再结合(4)式，不难得到