高考三角解答题“与面积、周长有关的问题”变式教学研究

陕西 安文华

高考三角解答题常见与面积、周长有关的问题，可以作为目标求值或求取值范围，也可以作为条件解三角形.解三角形是处理三角形的边角关系的有效手段，将面积与周长置于问题中，可使题目更加综合和灵活，更方便一题多变、一题多解的变式教学.

1.研究背景——三角解答题在高考中的考查特点

新课标、新高考实施以来，高考对三角函数的考查呈现出新的特点.一是三角试题的总体题量有所控制，如：2021年全国甲卷、乙卷均无三角解答题，理科试题仅一个选择一个填空，文科试题一个选择一个填空.2021年新高考Ⅱ卷只有一个三角解答题，没有选择填空题.二是部分试卷有结构不良三角解答题，如：2021年北京卷第16题、2020年新高考Ⅰ卷第17题、2020年北京卷第17题.三是解答题的考查以正、余弦定理的应用为主，无论题目初始条件或目标状态是否涉及面积与周长，其本质仍然是解三角形.

2020-2021年高考试题三角解答题知识考点

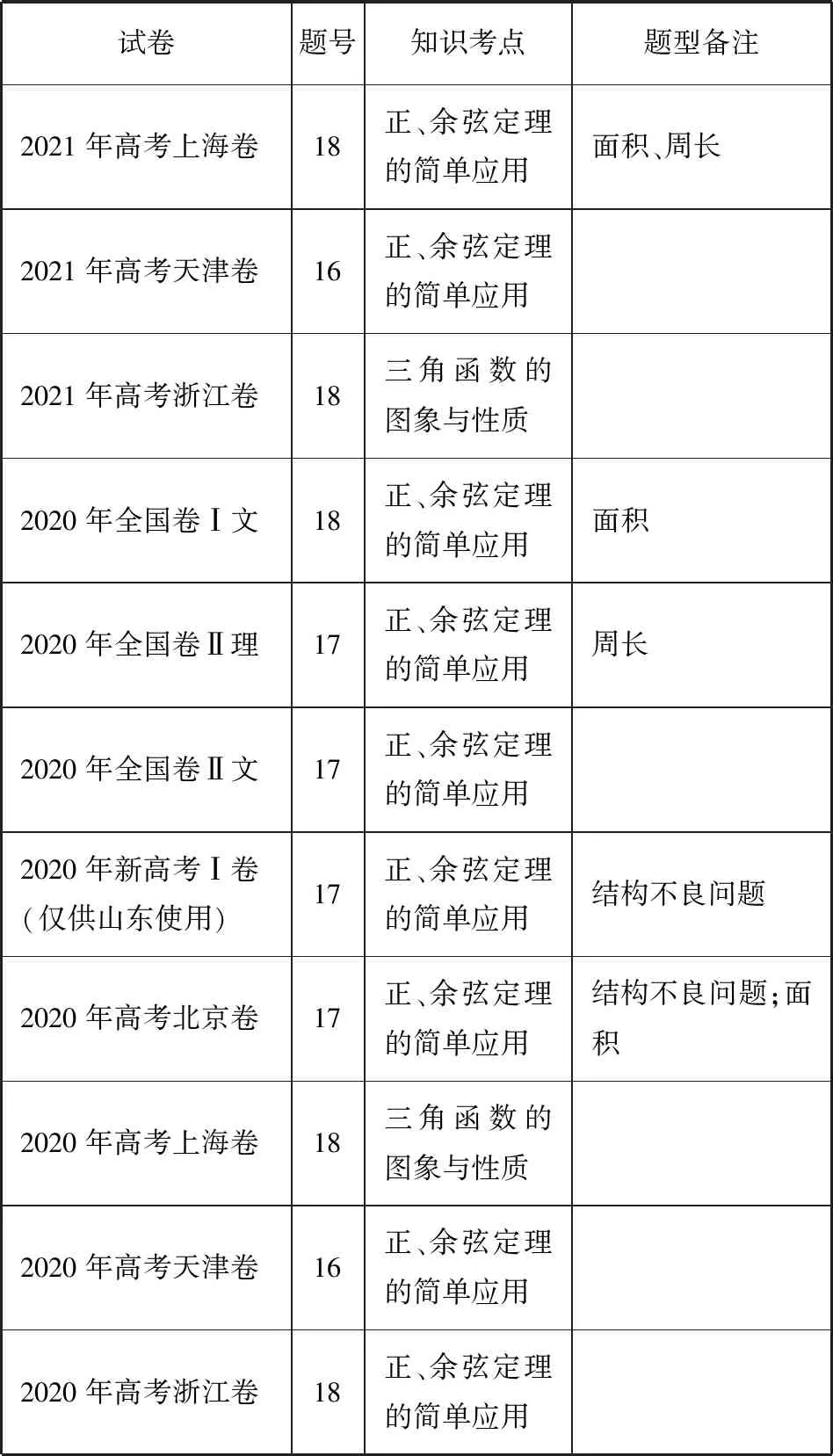
续表

2.研究目标——三角解答题“与面积、周长有关的问题”

我们知道高考三角解答题主要考点为正弦定理、余弦定理的简单应用，即解三角形，解三角形的本质是测量，是在三角形的边与角及面积、周长等基本量中给出若干求其他量或者其他量的取值范围.知识方面，正、余弦定理反映了三角形边与角的基本关系.能力方面，通过边角互化、三角恒等变形、代数运算、数形结合，能够反映考生逻辑推理、数学运算、直观想象的核心素养.

三角形是最基本的几何图形，三角是连接几何与代数的桥梁，通过边角关系、面积与周长，能够构建三角形的几何特征及相关数量关系，与面积、周长有关的问题相当于边角关系“高阶”问题，能够更加综合地联系各知识点，对学生阅读理解能力、信息整理能力、分析问题及解决问题的能力有更高的要求，在复习备考中以这些问题为主线能更有力的组织变式教学，更深入地理解相关知识，更熟练地掌握运算方法和技巧.

3.解题探究——母题及变式题解法探究

我们知道，在高考复习中，一轮复习：以知识为主，解题巩固.二轮复习：以解题为主，知识再现.在教学中进行一题多解、一题多变的训练，是为了加深学生对知识及相互联系的理解，提高学生的思维迁移能力和解题能力.在教学中进行一题多变的训练，常规思路有：追根溯源，在充分挖掘考点和题源的基础上，开展变式训练；通过设计与母题的条件、情境类似的问题，开展变式训练；通过变换问题的提问方式，开展变式训练.

3.1 已知对边对角

【例1】(2020·全国卷Ⅱ理·17)△ABC中，sin2A-sin2B-sin2C=sinBsinC.

(1)求A；

(2)若BC=3，求△ABC周长的最大值.

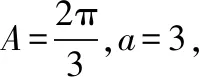
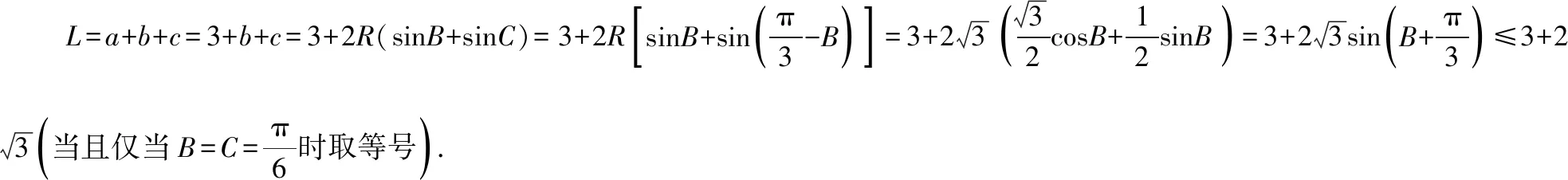
方法二：由余弦定理得a2=b2+c2-2bccosA，

【变式】上题中求△ABC面积的最大值.

方法二：由余弦定理得a2=b2+c2-2bccosA，

所以9=b2+c2+bc≥3bc，即bc≤3(当且仅当b=c时取等号)，

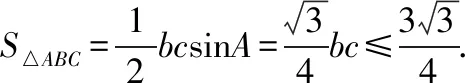
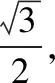
我们可以看到求面积或求周长这两个方向总是类似的，在这样的问题和变式求解过程中，方法一可以由正弦定理将目标表示为角的一元函数求值域.方法二也可以由余弦定理构造b+c与bc的关系，核心是将它们作为整体来看，通过基本不等式将“和”与“积”的关系相互转化.方法三是结合几何意义来判断和估算，作为代数求解的辅助和检验手段，起到相互印证的作用.这样的考法在历年高考题中是较经典的，如下题：

【例2】(2013·全国卷Ⅱ理·17)△ABC的内角A,B,C的对边分别为a,b,c，已知a=bcosC+csinB.

(1)求B；

(2)若b=2，求△ABC面积的最大值.

【变式】上题中求ac的最大值.

所以由一题多解的变式训练可以帮助学生解一道题，会一类题，发现问题的最优解.

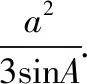
(1)求sinBsinC；

(2)若6cosBcosC=1,a=3，求△ABC的周长.

【例4】(2016·全国卷Ⅰ理·17)△ABC的内角A,B,C的对边分别为a,b,c，已知2cosC(acosB+bcosA)=c.

(1)求C；

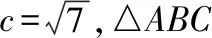
上述例3，例4就是在已知对边对角的条件下补上面积的条件来求周长，作为代数运算的方法，将两边之和与两边之积看作整体是常用技巧.

3.2 已知一边一角

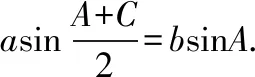
(1)求B；

(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

变式练习可以求△ABC周长的范围.通过一题多解、一题多变，可以在复习过程中用一个题目将散落的知识点像珍珠一样串起，让这些刻板的知识变成鲜活的经验，让这些工具在使用过程中磨砺出无往不利的锋芒.

3.3 已知一边及另两边之比

我们知道，已知一边为定值，又知另两边之比，则这两边公共顶点的轨迹为“阿氏圆”，在此条件下，可以求解三角形面积或周长的范围，当然如果还有其他条件，则变成求值问题.

【例6】(2021·上海卷·18)已知△ABC中，A,B,C所对边分别为a,b,c，且a=3,b=2c.

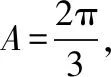
(2)若2sinB-sinC=1，求△ABC的周长.

【变式】△ABC的内角A,B,C的对边分别为a,b,c，且bccosC+c2cosB=2ab.

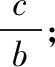
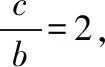
方法一：由①出发，记△ABC的面积为S，

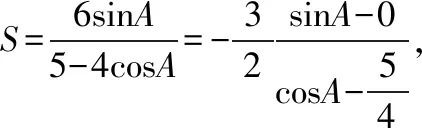
这样发散思维的好处是勾连起各个知识点，如二次函数、正弦型函数、解析几何等内容，开阔视野和思路，为学生建立起路路通、路路达的信心，起到综合复习的效果.

3.4 已知一边及另两边之和

如果已知一边及另两边之和，则这两边公共顶点的轨迹为椭圆.

(1)求cosB；

(2)若a+c=6，△ABC的面积为2，求b.

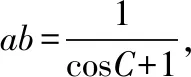
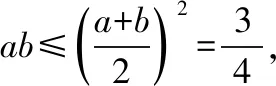
这里代数解法的特点仍然是关注a+b与ab的关系，难点是控制角C的范围，而条件较隐蔽，正是有了椭圆的几何意义使得我们可以在预知答案的前提下克服思维的盲区和漏洞.

【变式2】在①△ABC的周长为6，②asinB=2，③ab=4这三个条件中任选一个，补充在下面问题中.若问题中的三角形存在，判断△ABC的形状；若问题中的三角形不存在，说明理由.

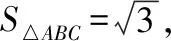
本题为结构不良问题，若选①，则有

其中，c=2,a+b=4的几何意义为点C在以A,B为焦点的椭圆上，由几何意义可判断△ABC的存在性(略)，下面进行证明.

c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)，即ab(cosC+1)=6,

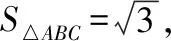
此时△ABC为等边三角形.

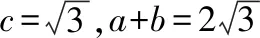
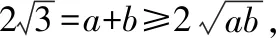
若选③，则得到此时△ABC为等边三角形(解略).

本题以已知一边及另两边之和为例，结合几何意义得椭圆的轨迹，由数形结合的方法能够更直观地判断解的存在，这是我们分析问题、解决问题的依据，先有信念上的判断，后有逻辑的证明，是因为我们信，才加以逻辑证明，在发现与提出问题、分析与解决问题这“四能”的培养过程中，逻辑推理固然重要，直观想象更应得到重视.结构不良问题具有多种评价解决方法的标准，在确定恰当的行动方面，没有明确的方法，需要学习者表达个人对问题的观点或信念，对促进学生素养的养成和能力的提升具有深远意义.

4.解三角形内容的备考建议

三角是联系几何与代数的桥梁，三角与向量、复数、平面几何、立体几何、解析几何、参数方程与极坐标等数学知识有着较为紧密的联系，高考中呈现了这一内容的基础性、综合性和应用性的特点.