变式为金链 模型是核心 进阶是关键——条件概率与全概率公式单元的变式思考

浙江 何晓禹 余继光

《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)要求，在概率教学中，应引导学生通过具体实例，理解随机事件独立性与条件概率之间的关系，能进行简单计算.为此，条件概率、乘法公式与全概率公式复习的重要途径就是选取经典问题，从不同角度拓展形成变式题，让学生理解随机事件独立性与条件概率的联系，尽可能挖掘课本例习题对建立条件概率概念的重要性，课本习题是教材编写者精挑细选后才定下的，具有鲜明的导向性、典型性、基础性等特点，在巩固、培养和发展学生对随机事件的独立性与条件概率概念的理解具有举足轻重的地位和作用.

变式教学是中国基础教育的精髓，变式问题串是变式教学的物质基础，数学教学中实施变式教学必须研究变式问题串.概率知识是有系统的，有结构的，引入变式教学后，实现由“反复练习”向“理解学习”的转变.变式问题串通过自己的系统与结构，揭示概率知识系统与逻辑结构.通过问题串进行变式教学可以多角度理解条件概率概念，有层次地推进乘法公式与全概率公式的教与学，在有序问题解决途径指引下，经过有层次的变式训练，使学习者对条件概率概念和思想方法得到理解与掌握.

1.随机事件的独立性

1.1 研究目标及背景

在复习随机事件的条件概率之前，先复习随机事件独立性，通过课本经典问题理解随机事件独立性概念——什么是随机事件的独立性？如何判断随机事件的独立性？2021年新高考数学概率题背景就是抽球模型中的随机事件独立性.

母题选取：一个袋子中装有标号分别是1，2，3，4的4个球，除标号外没有其他差异，

(Ⅰ)(2019年人教A版普通高中教科书数学必修二第246页试验2)采用有放回方式从袋中任意摸出两球，设A=“第一次摸到球的标号小于3”，B=“第二次摸到球的标号小于3”，分别计算P(A)，P(B)，P(AB)，你有什么发现？

(Ⅱ)(2019年人教A版普通高中教科书数学必修二第248页例1)采用不放回方式从中任意摸球两次，设事件A=“第一次摸出球的标号小于3”，事件B=“第二次摸出球的标号小于3”，那么事件A与事件B是否相互独立？

解题探究：(Ⅰ)首先明确样本空间Ω={(m,n)|m,n∈{1,2,3,4}}，

A={(1,1)，(1,2)，(1,3)，(1,4)，(2,1)，(2,2)，(2,3)，(2,4)}，

B={(1,1)，(1,2)，(2,1)，(2,2)，(3,1)，(3,2)，(4,1)，(4,2)}，

AB={(1,1)，(1,2)，(2,1)，(2,2)}

观察发现P(AB)=P(A)P(B)，定义具有这一特征的两个事件A与B，称其相互独立.

(Ⅱ)样本空间Ω={(m,n)|m,n∈{1,2,3,4}，m≠n}，

A={(1,2)，(1,3)，(1,4)，(2,1)，(2,3)，(2,4)}，B={(1,2)，(2,1)，(3,1)，(3,2)，(4,1)，(4,2)}，

此时P(AB)≠P(A)P(B)，因此事件A与事件B不相互独立.

1.2 变式角度分析

从上述问题发现，有放回抽样与无放回抽样、样本空间情境的变化对事件独立性有着直接影响，在具体操作过程中，通过计算事件积的概率来判断事件独立性，因此，变式角度，一是问题情境；二是有、无放回抽样；三是样本空间容量大小变化，一般而言，数学命题专家会在这几个方面进行变式.

变式方向一：小球个数增加，有放回抽样条件下，关注随机事件间的独立关系.

【变式1】(2021·新高考Ⅰ卷·8)有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则

( )

A.甲与丙相互独立 B.甲与丁相互独立

C.乙与丙相互独立 D.丙与丁相互独立

解题探究：首先要知道两个事件相互独立的概念，

由于P(甲丁)=P(甲)P(丁)，故选B.

解读：这是根据教材一枚骰子投掷两次所形成的36个基本事件而设计的一个检测独立性概念的题，此题说明，高考命题专家以小球为抓手，问题情境对所有人公平.

变式方向二：小球个数增加，无放回抽样条件下，关注随机事件间的独立关系.

【变式2】有6个相同的球，分别标有数字1，2，3，4，5，6，从中不放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则

( )

A.甲与丙相互独立 B.甲与丁相互独立

C.乙与丙相互独立 D.丙与丁相互独立

解题探究：方法一：利用两个事件相互独立的直观意义判断，即如果事件A和B的发生互相不受影响，则事件A和B是相互独立的，否则不独立，

根据题意，可以判断样本空间Ω={(m,n)|m,n∈{1,2,3,4,5,6}}共有36个样本点，

对于事件甲所包含的样本点为A={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)};

对于事件乙所包含的样本点为B={(1,2),(2,2),(3,2),(4,2),(5,2),(6,2)};

对于事件丙所包含的样本点为C={(2,6),(3,5),(4,4),(5,3),(6,2)};

对于事件丁所包含的样本点为D={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}.

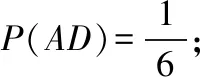
方法二：利用独立的一般定义，

于是P(AD)=P(A)P(D)，故选B.

变式方向三：改变问题情境，判断随机事件间的独立性.

【变式3】设甲、乙、丙三组纺织机器，已知在某一小时内，甲、乙都出现故障的概率是0.05，甲、丙都出现故障的概率是0.1,乙、丙都出现故障的概率是0.125.且甲，乙，丙三组机器分别出现故障的概率为0.2，0.25，0.5，则

( )

A.甲与乙相互独立，但乙与丙不独立

B.甲与丙相互独立，但甲与丙不独立

C.乙与丙相互独立，但甲与乙不独立

D.甲、乙、丙两两独立

解题探究：已知P(甲)=0.2，P(乙)=0.25，P(丙)=0.5，且P(甲乙)=0.05，P(甲丙)=0.1，P(乙丙)=0.125，

由于P(甲乙)=P(甲)P(乙)，

P(甲丙)=P(甲)P(丙)，

P(乙丙)=P(乙)P(丙)，

所以甲、乙、丙两两独立，故选D.

1.3 变式规律及研究

上述问题串说明，变式命题主要是对问题的样本空间和问题情境进行改变，检测应试者判断随机事件独立性的能力，解决问题的基本功是事件的古典概率计算，近期新高考数学概率相关问题着力点在随机事件独立性方面.

2.随机事件的条件概率

2.1 研究目标及背景

现实问题情境中，大量的随机事件是不独立的，特别是在某一事件发生的前提下，对另一事件的影响的可能性，就需要研究条件概率，根据《课程标准》水平测试要求，随机事件的条件概率的研究目标如下，

①结合古典概型，了解条件概率，能计算简单随机事件的条件概率;

②结合古典概型，了解条件概率与独立性的关系;

③结合古典概型，会利用乘法公式计算概率;

④结合古典概型，会利用全概率公式计算概率.

母题选取:(2019年人教A版普通高中教科书数学选择性必修第三册第45页问题2)假定生男孩和生女孩是等可能的，现考虑有两个小孩的家庭，随机选择一个家庭，那么

(Ⅰ)该家庭中两个小孩都是女孩的概率是多大？

(Ⅱ)如果已经知道这个家庭有女孩，那么两个小孩都是女孩的概率又是多大？

解题探究：记男孩为b，女孩为g，样本空间为Ω={bb，bg，gb，gg}，且所有样本点是等可能的，记A={选择的家庭中有女孩}={bg，gb，gg}，B={选择的家庭中两个小孩都是女孩}={gg}.

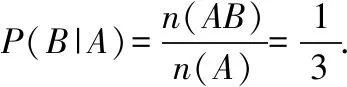
此例揭示：研究条件概率，要关注随机现象中的事件A，B，积事件AB是什么？样本空间的变化，样本容量有多大？此问题可以归结如下数学模型：

某袋内有1个白球1个黑球，从中接连取二次，每次取一球，取后放回，问二个都是白球的概率是多少？

2.2 变式角度分析

由于现实社会中，随机现象的复杂性，要从复杂的现实情境中剥离出具体事件，随机事件的条件概率涉及积事件概率；样本空间的变化；样本容量——具体与一般的变化，抽样方式——放回或不放回的变化；具体数据与一般数据的变化等等，因此，变式角度非常丰富，创新思考的意识要非常强.

类型一 随机事件的条件概率

变式方向一：理解条件概率概念及概率表达形式的区别.

【变式1】假设有2个事件A，B，且P(A)>0，P(B)>0，则下列结论一定成立的是

( )

A.P(AB)≤P(B|A)

B.P(AB)=P(A)P(B)

C.P(B|A)=P(A|B)

D.P(B)=P(B|A)

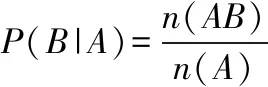
根据条件无法判断事件A与B独立，所以选项B不一定成立；

此变式在于评价学生对条件概率概念的理解及逻辑推理能力.

变式方向二：增加样本空间容量，体验条件概率计算方法.

【变式2】袋子中有10个大小相同的小球，其中7个白球，3个黑球，每次从袋子中随机摸出1个球，摸出的球不再放回，求:

(Ⅰ)在第1次摸到白球的条件下，第2次摸到白球的概率；

(Ⅱ)两次都摸到白球的概率

解题探究：以Ai表示“第i次取得白球”，i=1，2.

此变式在于学生体验条件概率与积事件概率的计算过程.

类型二 乘法公式的应用

变式方向三：在抽象数据条件下，体验乘法公式的计算方法.

【变式3】(一般模型)某袋内有a(a≥2)个白球b个黑球，从中接连取三次，每次取一球，取后不放回，问三个都是白球的概率是多少？

解题探究：以Ai表示“第i次取得白球”，A1=(白球，球，球)，A2=(球，白球，球)，A3=(球，球，白球)，这里“球”不论是白是黑均可，

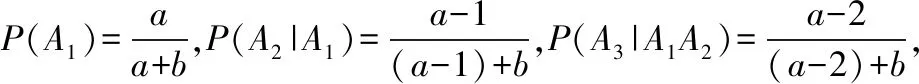
以Ai表示“第i次取得白球”，i=1,2,3，要求P(A1A2A3),

此变式提升数据的抽象性，以及积事件概率计算的一般模型.

类型三 全概率公式的应用

变式方向四：在具体数据条件下，体验全概率公式的计算方法.

【变式4】(具体数据)已知甲箱内有3个白球2个黑球，乙箱内有2个白球3个黑球，现从甲箱中任取一球放入乙箱，然后从乙箱中任取一球，则事件A：“从乙箱中取得白球”的概率为

( )

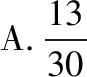
解题探究：以H1(H2)表示事件“自甲箱中取出的球为白(黑)球”，

此变式在于学生体验利用全概率公式解决问题的一般计算过程.

变式方向五：在抽象数据条件下，理解全概率公式的计算方法，检测代数式运算能力.

【变式5】(抽象数据)已知甲袋内有a个白球b个黑球，乙袋内有c个白球d个黑球，a,b,c,d∈N*，现从甲袋中任取一球放入乙袋，然后从乙袋中任取一球，求事件A：“从乙袋中取得白球”的概率.

解题探究：以H1(H2)表示事件“自甲袋中取出的球为白(黑)球”，考虑在H1，H2出现时，事件A的概率,

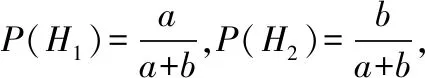
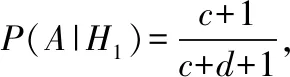
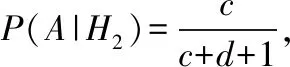
此变式在数据抽象状态下，全概率公式应用的一般模型.

变式方向六：改变问题情境，贴近现实，体验全概率公式的应用，这是用数学眼光观察世界教育理念的落脚点，引导学生用数学的思想方法解决现实问题.

【变式6】(情境转变)飞机机组由一架长机两架僚机组成，一同飞向某目的地进行轰炸，但要到达目的地，一定要有智能导航系统，而只有长机有此设备，一旦到达目的地，各飞机将独立进行轰炸，且每架飞机炸掉目标的概率均为0.3，在到达目的地之前，必须经过导弹阵地上空，此时任一飞机被击落的概率为0.2，求目标被炸掉的概率.

解题探究：三架飞机飞往目的地去轰炸时，必须经过导弹阵地上空，任一飞机被击落的概率为0.2，因此有以下各种可能：

(1)在导弹阵地上空长机被击落，此时按题意不管僚机是否被击落，都不可能有飞机到达目的地了；

(2)在导弹阵地上空两架僚机都被击落，只有一架长机没有被击落，此时只有一架长机到达目的地；

(3)长机没有被击落，其中一架僚机被击落，此时有两架飞机到达目的地；

(4)三架飞机均通过导弹阵地上空而到达目的地.

首先，对现实情境中的事件进行梳理：

设B0={没有飞机到达目的地}，B1={只有长机飞到目的地}，

B2={长机与一架僚机飞到目的地}，B3={三架飞机都飞到目的地}，

A={目标被炸掉}，

其次，对问题中数据进行表达：

P(B0)=0.2，

P(B1)=0.8×0.2×0.2=0.032，

P(B3)=(0.8)3=0.512，

P(A|B0)=0，P(A|B1)=0.3，

P(A|B2)=1-0.7×0.7=0.51，

P(A|B3)=1-0.7×0.7×0.7=0.657，

此变式创设复杂的现实情境，检测学生利用全概率公式来解决实际问题的能力.

类型四 复杂现实情境的综合应用

变式方向七：改变问题目标研究方向，在解决目标问题过程中，运用全概率公式，计算条件概率.

【变式7】(寻找原因)已知甲箱内有3个白球2个黑球，乙箱内有2个白球3个黑球，丙箱内有2个白球2个黑球，现任取一箱，再从箱中任取一球，结果发现是白球，则在事件A“此球为白球”条件下，事件H1“此球属于甲箱”的条件概率P(H1|A)为

( )

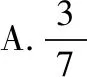
此变式既学会运用全概率公式计算概率，又会寻找原因，计算条件概率.

变式方向八：将教材中学到的思想方法用于解决现实问题，并在解决问题过程中运用全概率公式，这是新高考数学命题的基本理念.

( )

解题探究：首先，对现实情境中的事件进行梳理：

记A为“迟到”，H1,H2,H3，H4分别表示“乘飞机”“乘船”“乘汽车”“乘高铁”，

其次，对问题中数据进行表达：

此变式创设复杂的现实情境，检测学生利用全概率公式来解决实际问题的能力.

2.3 变式规律及研究

随机事件的条件概率、乘法公式、全概率公式应用变式设计，以小球为抓手，由易到难，然后改变情境，贴近现实.正如前面所言，此类问题变式角度颇多，呈现形式多样，问题情境多变，然而，所有问题的解题探究思路的顺序是固定的，即第一步，审题过程中，将问题中的随机事件寻找出来，排列好，并用数学符号表达好；第二步，将随机事件的概率与条件概率，从问题中寻找到，表达好；第三步，将问题情境中需要解决的问题寻找出来，表达好.

3.总结