着眼数据分析 回归概率本源

广东 武 静 韩 鹏

在教学过程中，我们从大量的实际背景中抽象出了两点分布、超几何分布、二项分布的模型，也抽象出了古典概型和几何概型等概率模型，但如何在具体的实际背景中求解概率、判断相互独立事件，分辨这些概率分布模型，对学生而言既是易错点，也是难点.学生因为对概率分布的规律性与随机性认识不到位，容易陷入“经验为主”的误区，忽略对数据的提取加工.

1 引例

【例1】(2021·新高考Ⅰ卷·8)有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球.甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则

( )

A.甲与丙相互独立 B.甲与丁相互独立

C.乙与丙相互独立 D.丙与丁相互独立

1.1 易错分析

本题中的易错点在于学生单凭“经验”，判断两事件是否相互独立.例如，感觉事件甲“第一次取出的球的数字是1”的发生并不影响事件丙“两次取出的球的数字之和是8”的发生而选A.

两个事件之间是否相互独立有时可根据实际含义做出判断，但有时仅根据实际含义是不能判断的，需要用独立性的定义判断.因此，判断两个事件是否相互独立，凭借经验并不可靠，应该学会用数据说话，用定义来判定相互独立事件.

1.2 解答过程

【分析】判断两个事件是否相互独立，脱离对概率的数据分析，单凭经验有可能会出错，因此利用定义P(AB)=P(A)P(B)来判断两个事件是否相互独立是最行之有效的方法.

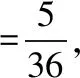
因为P(甲丙)=0，P(甲丙)≠P(甲)P(丙)，所以甲与丙不相互独立；

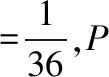
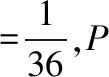
因为P(丙丁)=0，P(丙丁)≠P(丙)P(丁)，所以甲与丁不相互独立，故选B.

2 概率分布易错点拓展

离散型随机变量及其分布一直是高考命题的必考知识点，试题的背景在不断创新，但对基础知识和基本技能的考查是亘古不变的.2021年新高考Ⅰ卷随机变量及其分布的试题注重双基，着眼数据分析，回归概率概念本源，如第8题的相互独立事件，第18题的分布列等，这为一线教师的教学与备考指明了方向.概率分布模型的研究原则都是从直观到抽象，先定性后定量，但是，由具体实例如何建立概率分布模型，对初步接触概率分布模型的学生来说存在认知上的困难.笔者在教学实践中发现，针对这一章节内容，学生经常忽略数据带来的信息，出现概念混淆、方法选择障碍、概率分布模型错位等问题.

2.1 条件概率

【例2】一个家庭中有两个小孩，已知其中有一个是女孩，则这时另一个是女孩的概率是

( )

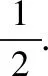
【分析】本题学生出错的地方在于忽略了已知其中有一个是女孩的样本点(女男)，(男女)的顺序，造成事件A包含的样本点只有两个：一男一女和两女.本题的一个家庭中有两个小孩对应的样本空间Ω={(男男)，(女男)，(男女)，(女女)}，每个样本点的发生是等可能的，属于古典概型的范畴.在古典概型中，我们还可以用如下公式求解：

在教学过程中，可以让学生探讨：如何把上述计算条件概率的思想应用于其他的概率模型中，以得到更为一般的与计数无关的公式：

另外，在教学中我们还可以设置问题：事件A的发生会不会影响事件B发生的概率，我们可以用P(B|A)与P(B)是否相等来验证，为后面相互独立事件的定义的推导埋下伏笔.

2.2 古典概型与几何概型

【例3】已知方程x2+2ax+b2=0，若a是从[0,3]内任取的一个整数，b是从[0,2]内任取的一个整数，求此一元二次方程有实根的概率.

【错解】a是从[0,3]内任取的一个整数，b是从[0,2]内任取的一个整数，则试验的全部结果构成的样本空间：

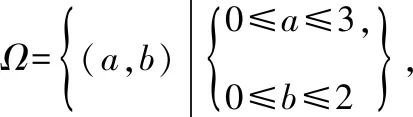
设一元二次方程有实根为事件A，由Δ=4a2-4b2≥0，化简得a≥b，事件A的样本空间：

【正解】由题意知，a∈{0,1,2,3}，b∈{0,1,2}，则所有的基本事件：

(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),共12种.

设一元二次方程有实根为事件A，由Δ=4a2-4b2≥0，化简得a≥b，事件A包含的基本事件：

(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),共9种,

【分析】本题中学生误以为a是[0,3]内的连续型随机变量，b是[0,2]内的连续型随机变量，因而将古典概型错判为几何概型.

在本题的教学中，我们可以针对离散型随机变量与连续型随机变量设置有效问题，如第一问中的a，b取区间的整数，第二问中的a，b取区间的实数，通过两个设问的鲜明对比，使学生明晰古典概型与几何概型的区别和联系.

2.3 两点分布

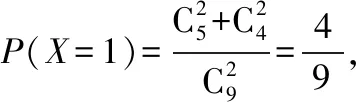
X12P4959

【分析】本题中学生对于两点分布的概念不清晰，只取两个不同取值的随机变量并不一定服从两点分布.两点分布的定义如下：

若随机变量X的分布列具有下表的形式，则称X服从两点分布(0-1分布)：

X01P1-pp

概率分布模型比较抽象，在实际教学过程中，我们可以从大量的具体案例出发，引导学生从大量案例的数据中分析归纳出两点分布模型的特点和含义，并结合学生自己实际举例.若学生举例的时候出现错误，例如本题中的分布模型，教师便可以引导学生：虽然随机变量X并不服从两点分布,但是可以通过适当的变换把它变成两点分布：

在多个结果的随机试验中，如果我们只关心某一个随机事件是否发生，就可以利用两点分布研究它.总之，两点分布不仅可以用来研究只有两个结果的随机试验的概率分布规律，也可以用于研究某一随机事件是否发生的概率分布现象.这些看似无用的教学过程，实则帮助学生理解两点分布的内涵和外延.

2.4 二项分布与超几何分布

【例5】为提高全民身体素质，加强体育运动意识，某校体育部从全校随机抽取了男生、女生各100人进行问卷调查，以了解学生参加体育运动的积极性是否与性别有关，得到如下列联表(单位：人)：

经常运动偶尔运动或不运动合计男生7030100女生6040100合计13070200

(1)根据以上数据，判断能否在犯错误的概率不超过10%的情况下认为该校参加体育运动的积极性与性别有关；

(2)用频率估计概率，现从该校所有女生中随机抽取3人.记被抽取的3人中“偶尔运动或不运动”的人数为X，求X的分布列.

【错解】(1)略 (2)X的所有可能取值为0,1,2,3，

【正解】(1)略;

所以X的分布列为

X0123P2712554125361258125

【分析】本题第二问中题设“用频率估计概率，现从该校所有女生中随机抽取3人”学生理解为从样本所有女生中抽取，错以为X服从超几何分布.当女生人数很大而抽取的女生人数较少时，每次抽取女生后，“偶尔运动或不运动”的概率近似不变，从而服从二项分布.

3 概率分布的教学策略

学生对篇幅较长的概率分布实际背景的阅读理解能力不足，对于概率分布模型的属性判断和转化能力不足，对相关的数据分析能力不足而导致易错，因此，我们在实际教学过程中，应注重基础知识和基本技能，回归概念核心，着眼数据分析与数学阅读指导，设置有效问题，突破概率分布的易错点.

3.1 激活数学教材，回归概念核心

高考试题是复习备考的风向标，2021年新高考Ⅰ卷试题中对概率分布的考查回归到基本的概念，如第8题的相互独立事件，为复习备考指明了方向.以往复习备考时，学生会买很多学习资料，陷入题海战术，反而忽略了手边最重要学习资料——教材.那么如何使用教材，夯实基础是摆在我们面前的最重要的问题.首先，落实教材，列知识点，画思维导图，找出教材中概率分布的主线——知识线、方法线；其次，整合教材，包括例题和课后习题，理清考核项、分析考核点，找出教材中概率分布的暗线——思想线、能力线，从而激活教材，创造性地使用教材，回归概念核心.

【例6】(2007版高中数学选修2-3习题2.2B组)某批n件产品的次品率为2%，现从中任意地依次抽出3件进行检验，问：

(1)当n=500,5000,50 000时，分别以放回和不放回的方式抽取，恰好抽到1件次品的概率各是多少？

(2)根据(1)，你对超几何分布与二项分布的关系有何认识？

本题通过产品数量500,5000,50 000以及放回与不放回的抽取方式，让学生学会用数据说话，通过不同的数据信息帮助学生理解超几何分布和二项分布之间的关系.

【答案】(1)当n=500时，

如果放回，这是二项分布，P=0.057 624，

如果不放回，这是超几何分布，P≈0.057 853;

当n=5 000时，

如果放回，这是二项分布，P=0.057 624，

如果不放回，这是超几何分布，P≈0.057 647;

当n=50 000时，

如果放回，这是二项分布，P=0.057 624，

如果不放回，这是超几何分布，P≈0.057 626.

(2)共同点：每次试验只有两种可能的结果：成功或失败.

不同点：①超几何分布是不放回抽取，二项分布是有放回抽取；

②超几何分布需要知道总体的容量，二项分布不需要知道总体容量，但需要知道“成功率”；

联系：当产品的总数很大时，超几何分布近似于二项分布.

3.2 设置有效问题，经历概念形成

两点分布、超几何分布、二项分布的概率分布模型的概念的教学需要通过具体实例概括其共性而得出.大量且丰富的生活实例，有助于学生理解这些抽象的概率分布模型.但如何在一节课的时限内融入生活实际，设置有效问题，让学生经历概念的形成过程便显得尤为重要.笔者建议先从简单的、可操作的背景入手，以设置有效问题串的形式让学生经历概念的形成，引导学生自主思考，激发学生把经验内化为能力.

例如，在学习n次独立重复试验和二项分布的时候，笔者设计了如下问题串：

抛一枚均匀的骰子，设事件A=“3点向上”.

问题1：抛骰子1次，事件A发生的概率.

问题2：抛骰子2次，事件A发生1次的概率.

问题3：抛骰子3次，事件A发生2次的概率.

问题4：抛骰子n次，事件A发生2次的概率.

问题5：抛骰子n次，事件A发生k次的概率.

教学过程中让一名学生做抛骰子试验，通过有效问题串引导学生通过不同次数的数据信息，分析多次试验结果之间的关系，层层递进，引导学生概括出n次独立重复试验和二项分布的概念.

3.3 着眼数据分析，提高转化能力

针对概率分布这一章节，学生出错的原因之一就是缺乏数据分析意识，捕捉不到题目中的关键数据信息，图表转化能力欠缺.

《普通高中数学课程标准(2017年版2020年修订)》指出，通过高中数学课程的学习，学生能提升获取有价值信息并进行定理分析的意识和能力.因此，在概率分布的概念教学过程中，留给学生自己动手实践的时间，让学生在已有的随机事件的概念基础上，提取数据→分析数据→建立数学模型→习得概念→应用模型，完成新知识的构建.学生经历了从已知到未知，从宏观到微观，从定性到定量，从理论知识到动手实践再到新知识的习得，使学生原有知识结构和经验按照新知识的生成过程重新组合.在这个过程中，除了概率分布的知识结构得到完善和发展，学生的动手能力、数据分析能力及知识的正向迁移能力和逆向思维能力等也得到提升.

3.4 加强阅读指导，提升应用能力