辅助角公式模型的几何解释及应用

天津 高成龙

辅助角公式模型是三角函数中的重要公式模型，它是两角和与差的正、余弦公式的逆用，它是将函数y=asinωx+bcosωx转化成y=Asin(ωx+θ)的唯一桥梁，它为研究这一类函数的性质提供了思路和方法.本文先给出辅助角公式的模型及证明，然后构造几何图形，从“形”的角度来解释“辅助角公式模型”，通过形与数的结合，让学生感悟数学知识之间的关联，加强对数学整体性的理解，进一步认识和理解辅助角公式模型的本质，最后运用辅助角公式模型对教材中的例题进行深入探究.

一、辅助角公式模型及其证明

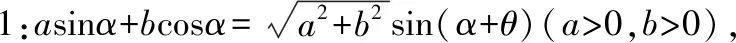
分析：由三角函数和差公式可以知道Asin(α+θ)=Acosθsinα+Asinθcosα，那么利用等式的性质可以知道asinα+bcosα必然也可以转化为Asin(α+θ)，因此辅助角公式模型是可行的.对于辅助角公式的证明方法比较多，下面利用待定系数法的原理给出辅助角公式的证明：

模型证明：

y=asinα+bcosα=Asin(α+θ)=Acosθsinα+Asinθcosα，

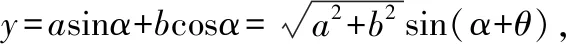
通过对辅助角公式模型的推导探究，引导学生把y=asinωx+bcosωx转化为Asin(ωx+θ)的形式，在变换过程中对变换现象和变换目标进行对比、分析，促使学生对解题过程中如何根据问题的条件进行变形，从而提高学生的逻辑推理、数学运算核心素养.

二、辅助角公式模型的几何解释

为了让学生更好地理解和应用辅助角公式，我们在实际教学中应该构造几何图形.从“形”的角度给出辅助角公式模型的几何解释.下面构造几何图形来解释辅助角公式模型.

如图，在Rt△ABC中，∠ACB=90°，CA=b,CB=a，直角顶点C在直线l上，设AC与直线l的夹角为α.由图可知，asinα+bcosα=DC+CE=DE，

如图，在Rt△ABC中，∠ACB=90°，CA=b,CB=a,直角顶点C在直线l上，设AC与直线l的夹角为α.由图可知，asinα-bcosα=CE-CD=DE，

点评：构造学生初中就熟悉的“直角三角形遇到直线”这一几何模型，从“形”的角度来解释“数”有助于学生更好地认识和理解辅助角公式的结构和本质.同时这样的设计也能突出代数运算与几何直观之间的融合，通过形与数的结合，能让学生感悟数学知识之间的关联，加强对数学整体性的理解，这也是《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)对代数与几何主题的要求.

三、辅助角公式模型的应用

1.例题呈现

分析：可先建立矩形ABCD的面积S与α之间的函数关系f(α)，再求函数S=f(α)的最大值.

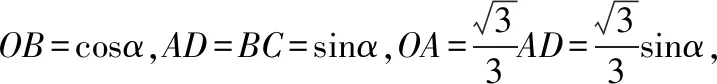
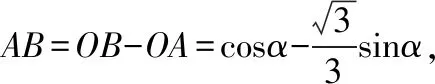
2.例题再探究

《普通高中教科书·教师用书》(以下简称《教参》)提出：对于例1，还可以去掉“记∠POC=α”，将设问改成“求矩形ABCD的最大面积”，现将例1改编呈现如下：

分析：将“∠POC=α”这一条件去掉增加了问题的难度，问题的改编可以培养学生在综合情境中提出运算问题和确定运算对象的能力，进一步培养学生的数学运算核心素养.另外学生在建立函数模型解决上述问题时对自变量又多一种思路,可以选择从“角”出发，也可以选择从“线段”出发.

思路1：从“角”出发

学生可以选择∠COB,∠OCB,∠COQ三个角中的一个作为变量α，进一步建立矩形ABCD的面积S与α之间的函数模型，即为教材中的例题，这里不再赘述.

思路2：从“边”出发

学生可以选择AD,OA,AB三条线段中的一个作为变量x，下面设AD=x，建立面积S与x的函数模型：

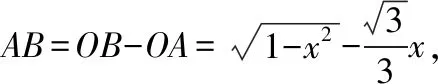
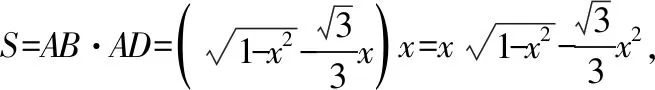
解法1：图象法

解法2：换元法

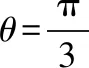
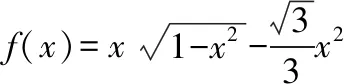
3.方法总结

当我们重新回顾、品味例2时，发现例2的求解可以很好地培养和提升学生的数学运算与数学建模核心素养.主要表现：

①以实际问题为例题，可以建立数学与生活的关联，进一步培养学生在综合情境中提出运算问题和确定运算对象的能力，进一步提升数学运算核心素养；

②通过思路1和思路2的解法比较，让学生感受到以角为自变量的优点，两种解法能让学生从不同角度入手去研究，培养学生能根据问题特点及运算的条件合理选择运算方法的能力；

③建立矩形ABCD的面积S与两种变量之间的关系可以培养学生的“数学建模核心素养”，另外在建立函数模型时，有两种自变量可供选择，可以促进学生对函数模型多样性的理解.