谈高三数学复习课教学
安徽 朱启州
从2019年至2021年高考数学命题从理念、结构到形式已经发生较大变化,特别是新高考卷,更加契合高中新课标要求,有力促进新教材的实施与新课标的落实.基于以上认识,本文就高三数学复习谈几点思考,供读者参考.
一、瞄定高中新课标要求,促进学生思维水平的提高
数学思维能力主要有逻辑思维能力、观察能力、直觉思维能力、空间想象能力等.数学教学应从学生已有的知识经验出发,让学生亲历知识的形成过程,获得对数学的理解,进而思维水平得到提高,实现数学创造能力和问题解决能力的提升,因此,数学复习课教学必然要以思维为核心,重视培养学生数学思维品质.

( )
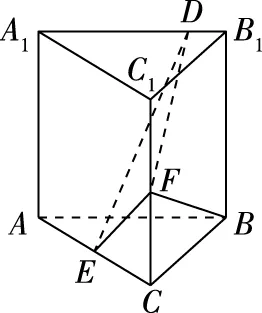
A.a C.b 当x∈(0,1)时,(1+x)2-(1+4x)=x2-2x=x(x-2)<0, 于是a>c,故选B. 高三数学复习往往以模型归纳为重点,将刷题作为提高应试水平的重要学习方式,比如流行的模型解题方法等.如果数学问题解决都用一个个数学模型给框住,那么数学教学就失去了自身的教育价值.因此,在数学复习教学中我们要给学生留足思考与想象的空间,让问题的解决过程成为学生研究数学的过程. 【例2】(2021·全国甲卷理·19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1. (1)证明:BF⊥DE; (2)当B1D为何值时,平面BB1C1C与平面DEF所成的二面角的正弦值最小? 【解析】(1)如图1,E为AC的中点,D为棱A1B1上的动点,DE⊂平面EA1B1,又AB∥A1B1,所以AB平行于平面EA1B1与平面ABC的交线为EM(M为BC中点),如图2,过EA1B1的直三棱柱ABC-A1B1C1截面就是A1B1ME,在矩形BB1C1C中易证得BF⊥MB1,难点得以突破. 图1 图2 图3 【点评】建立空间直角坐标系,通过向量的坐标运算来解决空间图形平行关系与垂直关系,利用向量法求解线线、线面、面面所成的角的问题,可避开几何法求解时烦琐的逻辑推理,学生解决这类问题已有现成的模型.立体几何问题的试题设计中几何法证明平行关系与垂直关系就是绕不过的坎,如何舍弃第一问,把(1)做结论,解第(2)问“BC⊥AB”是不可缺少的重要建系条件,如果都无法解出,得分可想而知.所以高三数学复习过程中,解题规律的归纳与总结是非常必要的,但是更为重要的是不要让模型框住学生的数学思维,应引导学生钻研数学,提高分析问题与解决问题的能力. 一题两空、多选题、结构不良试题等高考新题型已然常态化,要从发展学生思维的角度看待新题型,而不是从考试的角度去看,不要将新题型放到教学的对立面,复习中讲好、用好新题型对培养学生思维的发散性、知识迁移能力及思维灵活性有着重要作用. 【例3】(2021·新高考Ⅰ卷·11)已知点P在圆(x-5)2+(y-5)2=16上.点A(4,0),B(0,2),则 ( ) A.点P到直线AB的距离小于10 B.点P到直线AB的距离大于2 图4 图5 【点评】讲好、用好高考新题型,引导学生发散式思考,深入研究数学问题,对培养学生理性思维水平、创新能力与创新意识具有重要作用. 复习课教学中重视设计低起点、缓坡度、多层次综合性问题,满足不同层次学生的学习需求,让不同层次学生都得到发展,能有效激发学生的学习兴趣. (1)若a=1,求f(x)的定义域; (2)若a≠0,且f(ax)=a有2个不同实数根,求a的取值范围; (3)是否存在实数a,使f(x)在定义域内具有单调性?若存在,求a的取值范围. 【点评】此题综合考查学生函数与不等式的核心内容,既有一定的综合性,又具层次性,让不同层次的学生都能得到发展,让复习课面向全体学生,提高复习课的效益. 数学运算核心素养是学生“六大核心素养”的基础.高三数学复习切忌“眼高手低”,对于具有复杂运算的数学问题,要在教学前给出,让学生课前亲自动手解决,课中重点对不同解题路径进行点评,引导学生解题中用优解、巧算去解决问题,重视解题过程的优化. (1)求C的方程; 所以S∈(0,6],即当t=1时,四边形AMBF1的面积的最大值为6.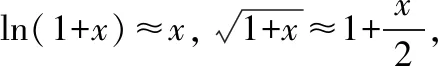


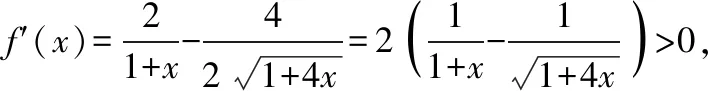



二、数学复习课教学要从模型的框子里跳出来



三、数学复习课教学要从发展学生思维的角度看待高考新题型





四、数学复习课教学综合性问题设置要“低起点、缓坡度、多层次”





五、重视解题过程的优化,提高运算能力









六、结束语


