一题一课，提升学生的数学学科核心素养

王菲菲

摘要：初中数学复习课中往往充斥着大量的习题，如何将复习课上得更有效率、更有趣味，收到复习课该有的帮助学生深入理解知识点的效果，值得每位数学教师深入思考。与其凌乱的知识点堆叠，不如深挖一道题目，通过一题串连知识点，引导学生进行发散学习。文章以“全等三角形”的复习课为例，一题一课，进行变式教学，提升学生的数学学科核心素养。

关键词：一题一课;全等三角形;变式教学;核心素养

在几何学习中，存在一些基本图形范式，教师要注重对基本图形的形式进行变化，让学生体会在变化的形式中不变的数学思想的，体验数学的整体性。笔者针对“全等三角形”复习课中的一道例题研发了一节“一题一课”讲评课，整理成文，以供研讨。

一、教学过程与思考

环节1：经典例题呈现。

例1如图1，AD=BD，AD⊥BC于点D，BE⊥AC于点E，AD与BE相交于点H。

（1）BH与AC相等吗？为什么？（2）连接ED，求证ED平分∠BEC。

教学预设：第（1）小题比较简单，大部分学生可以找到解题思路。在教学时，教师引导学生通过多种方式由AD⊥BC，BE⊥AC得到角相等的条件，由此证明△BHD≌△ACD。第（2）小题对于学生来说有一些难度，由于图1中没有涉及∠BED和∠CED的三角形全等，教师可以引导学生构造全等三角形来证明∠BED=∠CED。在此铺垫下，让学生小组交流讨论，梳理思路，教师跟进点评。

【设计意图】例1中的第（2）小题是服务于下文例2所增设的铺垫题。例1整体属于一道经典的中等难度题，作为这节课的开端，有利于帮助学生掌握相关知识。对于一些难度较大的习题，适当铺垫更有利于拓展学生的思维，更符合学生的认知规律，能使学生的思维过程更具有阶梯性和完整性。

环节2：形变质不变，感悟数学的变化美。

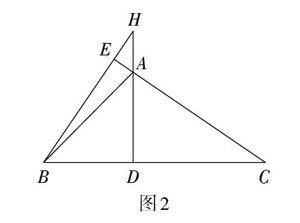
例2如图2，AD=BD，AD⊥BC于点D，过点B作CA的垂线，交CA的延长线于点E，DA的延长线与BE的延长线相交于点H。

（1）BH与AC相等吗？

（2）连接ED，求出∠DEH与∠ABD的数量关系。

教学预设：例1讲评结束，教师引导学生感悟图1

是如何生成的。首先是以含有45°角的直角三角板出发，画出等腰直角三角形ABD;其次，在直角边AD上任取一点H，连接BH并延长;最后，过点A作AE⊥BH于点E，交BD延长线于点C。那么，可以看出此时点H位于线段AD上，教师引领学生思考，若点H落在直线AD上，其他题干不变，例1中的第（1）小题的结论是否依然成立？此时学生可以轻松解决例2的第（1）小题，证明△BHD≌△ACD，得到BH=AC。

在例1第（2）小题的跟进讲评后，学生对DE的特殊位置已经有了一些了解，可以类比证明例2中DE平分∠BEC，然后得出∠BED=45°。那么∠DEH的大小及其与∠ABD的数量关系问题就迎刃而解了。

【设计意图】例2相较于例1而言，只改变了点H的位置，虽然改变了形式，但是题目结构与解题思路没有变化。例1与例2相结合进行讲解，有利于学生感悟数学的运动，让学生深刻了解数学知识的精神内涵和其中包含的統一的数学思想方法，有效提高课堂教学效率。

二、教学立意的进一步阐释

1.辨明结构，提升迁移能力

对于难度较大的几何题，首先要辨析题目所反映的真正内容，探析题目的结构，化陌生为熟悉。学生对问题结构的理解受到具体题目情境的限制，就事论事，从整体结构去理解题目结构存在困难，这是比较普遍的现象。在等腰直角三角形这节课中有大量的经典题型和结论可以与平面直角坐标系相结合。在教学此类题目时，教师应该从平时的点滴渗透，引导学生迁移相似情境，提升学生的迁移能力。

2.变式教学，渗透思想方法

由例1到例2，变换题目背景，进行变式教学。变式教学是通过有目的地变换条件或情境，以凸显数学概念或规律的本质属性的教学。让学生能在不同角度、不同层次、不同情形、不同背景下重新认识问题的本质。例2的题设对学生来说难度较大，而由例1引入，让学生可以自然地联想到例2可以转化为例1的基本图形，将复杂的题设简单化，提炼出最关键的问题，进而解决问题，这种转化与化归的数学思想在数学学习过程中是非常重要的。

数学思想是数学学习的根，是学生能够发现问题和解决问题的根本，没有数学思想方法的教学，是没有灵魂的，是浮于表面的。数学思想方法蕴涵于数学知识中。在平时教学中，教师潜移默化地渗透，才是帮助学生学习的有效方式，让他们掌握思想方法，学会思考。

三、结束语

总之，在解题教学中，教师应该精心设计“再发现”的情境，让学生能够透过现象看本质，使学生的学习经历认识形式变化的过程，在形式的运动变化过程中认识内容，体验数学研究的过程及数学思想方法的复习教学真谛。文章仅以此题为例，设计了一节蕴涵形式变化与思想方法的课堂，期待更多专家同仁的批评指正。

参考文献：

[1]章建跃，陶维林.注重学生思维参与和感悟的函数概念教学[J].数学通报，2009，48（6）.

[2]朱金祥，刘东升.数学教学中例题变式的策略：基于教学追问的视角[J].教育研究与评论（中学教育教学版），2016（9）.