基于问题导向的单元复习课深度学习教学设计——以《解三角形》为例

广东省汕头市澄海中学 (515800) 陈焕涛广东省佛山市顺德区容山中学 (528303) 潘敬贞云南师范大学信息学院 (650500) 唐明超

1.引言

单元复习课教学是高中数学的重要课型之一，完成某个单元的新课教学后我们都需要对本单元进行复习.单元复习教师的做法更多是回顾复习(本单元的概念、定理以及公式)、例题示范、试题训练的基本模式，不同教师虽然选取的例题与练习题有所不同，但教学活动大同小异.这种复习方式不仅耗时较长，而且问题意识不突出，知识碎片化依然存在，学生很难构建知识体系，也很难做到触类旁通，解题能力也难以得到有效提高.单元复习的核心目标是帮助学生梳理并整合基础知识，构建知识体系，最终提升解题能力，发展数学素养，以问题为导向的单元复习课教学却能很好的达成以上教学目标，实现深度学习.文章主要呈现用例题引导学生复习解三角形的基本概念、基本定理以及基本公式，用变式引领构建知识体系，用变式训练提升解题能力并发展数学核心素养，用一题多解拓宽解题思路培育创新意识的整个过程，试图建构一种指向深度学习的单元复习课教学模式，重点回答应该怎么做以及为什么这样做两个核心问题.

2.教学案例

2.1 用例题引领巩固双基

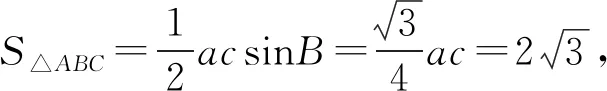
评注：例1属于基础问题，绝大部分学生都能快速解答，增强进一步探究学习的热情，容易调动学习积极性，提高学生参与度.符合由浅入深，由易到难的层级递进的探究与学习规律，能为进一步展开教学活动奠定良好基础.

设计意图：由于例题的解答用到了正弦定理、余弦定理、三角形面积公式、三角形内角和定理等知识，可以在解题时借机引导学生回顾复习相关知识点，可以达到回顾复习、梳理整合知识的目的，在反思小结阶段适当提炼升华可以有效深化难点并突出重点的作用.归纳基于问题背景以及转化与化归、方程等思想，经过运算、代换、推理，求解三角形未知的边、角及三角形有关问题的求解策略，积累解题经验，提升能力并培育核心素养.

2.2 基于问题变式构建知识体系

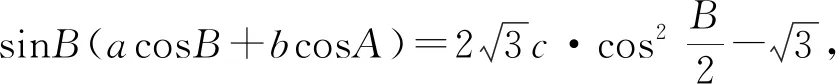
变式2 (串联同角三角函数基本关系)△ABC的内角A，B，C所对的边分别为a，b，c，已知2sinBtanB=3，求角B.

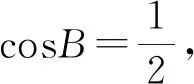
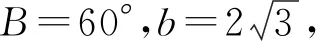
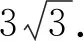
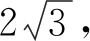
设计意图：基于以上4个变式问题可以有效达成复习降幂公式、同角三角函数基本关系、重要不等式、三角函数的性质等基础知识；进一步巩固了正弦定理、余弦定理、三角形面积公式以及内角和定理等知识，将各个知识点有效串联起来，构建知识体系，使知识网络化.同时进一步提升学生的代数变形能力，解决问题的能力等.

2.3 基于问题变式发展素养

变式6△ABC的内角A，B，C所对的边分别为a，b，c，若B=60°，△ABC外接圆的面积为4π，求△ABC周长的最大值.

变式8△ABC的内角A，B，C所对的边分别为a，b，c，已知D是边AC上一点，且AD=2CD，B=60°，a=2,a=3，求BD.

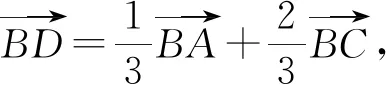
设计意图：变式5至变式8使得问题进一步深化，问题的求解对数学能力有了更高的要求，通过问题的解答过程可以有效巩固“四基”，发展“四能”，最终达到提高解题能力，发展数学素养的目的.

非营利组织一般都是以绿色营销模式为主，不断宣传和加强民众的绿色环保观念，非营利组织会要求在各种类型的公共服务以及产品的设计、研发、量化生产和消费等环节，都需要考虑到对环境的影响和社会公众的长远利益。所以，在低碳营销模式的发展过程中，非营利组织应该要积极配合有关政府部门的工作，以节约能源和保护环境为主旨，大力宣传低碳营销模式的理念。[4]从社会公众的角度考虑，非营利组织帮助消费者建立低碳消费观念，同时也帮助企业专注于低碳技术的研发生产和营销，促使消费者深入细致了解低碳营销模式的优势所在，更加自主地选择使用低碳产品，促使整个社会步入低碳经济的可持续发展的道路。

2.4 基于一题多解拓宽解题思路培育创新意识

变式9 在△ABC中，已知D是边BC上一点，且BD=2DC，AD=2，A=60°，求△ABC面积的最大值.

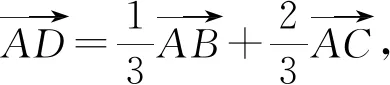
评注：解法1是本题的常规解法，也是众多学生容易想到的方法，但解答过对运算求解能力有比较高的要求；解法2结合平面向量基本知识，基于向量这个重要的数学工具使得问题解答过程思路清晰、逻辑推理过程简洁，优化运算并提高解题效率的作用.

设计意图：从不同角度整合不同知识点对同一个问题进行深化拓展，引导学生开展问题求解训练，在实际问题的解决过程中感悟数学问题的本质，寻找知识间的逻辑联系，优化学生思维，拓宽解题思路，培育创新意思.

3 高考链接

A.6 B.5 C.4 D.3

(1)求B；(2)若△ABC为锐角三角形，且c=1，求面积的取值范围.

真题4 (2018年全国卷Ⅰ)在平面四边形ABCD中，∠ADC=90°，∠A=45°，AB=2，BD=5.

设计意图：高考题是命题专家智慧的结晶，高考题不仅有很好的选拔功能，同时也有很好的教学功能，是教与学的好素材.因此，通过对问题的求解，回顾基础知识，构建知识体系后，再选取针对性较强的高考真题让学生在不同情景中解决问题，通过对不同问题的解题实践，提高学生的应变能力，增强学生学习数学的信心，训练数学思维，培育理性精神和发展数学素养水平等.

4 结语

由于学生刚完成本单元新知识的学习，往往缺乏将知识点连成线，继而织成面，应用所学知识解决实际问题的能力还有很大的提升空间，以问题的为导向的单元复习课教学模式是以问题为驱动，引导学生回顾并复习知识，构建知识体系，使知识系统化网络化.通过对典型问题开展变式拓展并从不同角度思考问题、解答问题可有助于提升解题能力，培育创新意识，发展数学核心素养，最终达到预期的教学效果.