基于收敛思维的变式教学实践与思考
——以解析几何复习课为例
福建省莆田第二中学 (351131) 卢 妮 谢晓琼
一、问题的提出
收敛思维就是思维主体把从不同渠道得到的各种信息聚合起来,重新加以组织,使之明确无误地指向一个(或一种)选择.多题归一实际上就是收敛思维.在无边高考数学解析几何复习过程中,对于“形异质同”的问题,教师需要深刻地挖掘其本质,以本质为核心统领这些问题,跳出题海,来到“变式”的岸,才能让学生在考试中面对不同的问题情境时立于不败之地.变式教学中如何帮助学生从变化多端的“形”,抓住不变的“质”呢?本文就基于收敛思维的的变式教学结合高考数学解析几何复习课的课堂教学实践案例谈谈一点自己的想法.
二、教学案例
“问渠哪得清如许,为有源头活水来”,高考题目源于教材,又高于教材,因此高三复习课有必要回归教材,选取有代表性、重点突出的典型问题,有意识地进行一题多变训练,引导学生从变化的问题形式中找出不变的规律,发展学生分析问题和解决问题的能力.
1.回归教材

图1
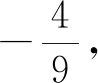
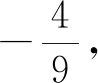
点评:这是一道典型的求轨迹方程.条件涉及动直线的斜率是定值,对题目适当的变式就可以变出更多的类似题目.


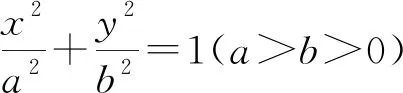
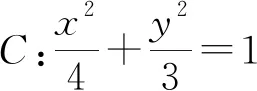
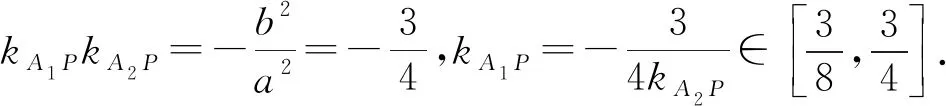

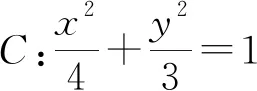
分析:由结论1,A,B两点关于原点对称,即直线AB过定点(0,0).

图2
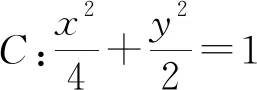
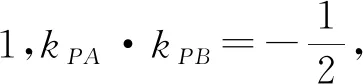
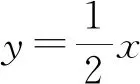

图3

图4


2.聚焦高考
案例2 (2015年全国卷理科Ⅱ卷第20题)已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.
(Ⅰ)证明:直线OM的斜率与l的斜率的乘积为定值;(Ⅱ)略.

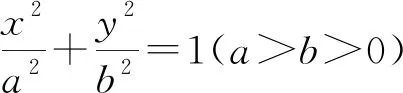
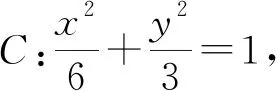

图5
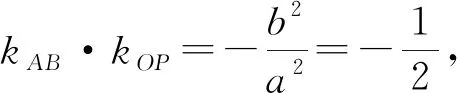
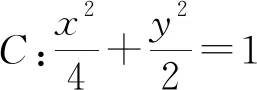

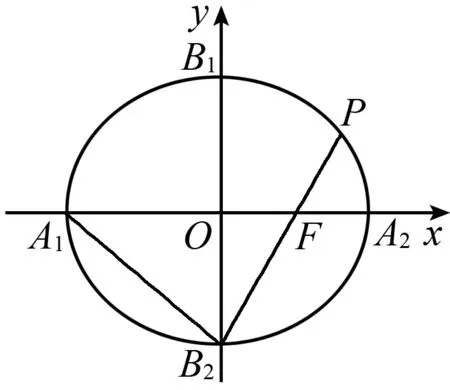
图6

案例剖析:定点定值问题是圆锥曲线中十分重要的研究课题,蕴含着动、静依存的辩证关系,深刻体现了数学的魅力,在高考中常常涉及此类问题且位于中档题的位置.通过案例2将上述结论2的探究方法(设点法,点差法等)以及结论2都得到了运用,起到了典例示范的作用,并通过二种方法的对比训练学生发现中心弦特征;挖掘弦中点的方法技巧;真正起到学以致用的作用.从具体问题入手,通过对解决方法进行总结辨析,渗透了转化与化归的思想,使学生能够根据问题的条件寻找与设计更合理、更简捷的运算途径,并引导学生发现这类问题所具有的更一般性规律.
三、教学思考
美国著名数学家波利亚曾说:“一个专心的认真备课的教师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域”.[1]在高考数学复习课教学,若没有明确而有效的教学策略指导,学生容易缺失学习的积极主动性,复习课有可能就变得高强度低效率.纸上得来终觉浅,绝知此事要躬行,所以高三复习课要紧扣大纲,立足教材,聚焦高考,选取重点突出的问题,通过强化、类比、拓展、延伸、迁移的问题变式题组教学,促使学生成功跨越“最近发展区”,点点突破,层层推进,步步深入,培养学生的问题归纳、概括总结能力.而在一题多变题目演示下,学生的思维灵活性也能够得到拓展.在解析几何求解过程中,不断提升学生的数学运算、逻辑推理等核心素养,从而使得数学核心素养内化于心.让学生体会问题的通法,进而提炼思想方法,使学生做一题会一片通一类,使学生能真正做到以不变应万变,笑傲高考考场.

