一道测试题的解题探索与思考

江苏省无锡市洛社高级中学 (214000) 冯宇斌

波利亚说过“掌握数学就意味着学会解题”.解题是学生学好数学的必要途径，同时也是课堂教学的重要组成.要做好解题教学工作，教师首先要学会解题，学会研题.以此为基，辅以适时适量的活动设计，学生才能逐渐学会解题，逻辑推理等核心素养也随之孕育发展.本文呈现笔者对一道测试题的整个探究历程，抛砖引玉.

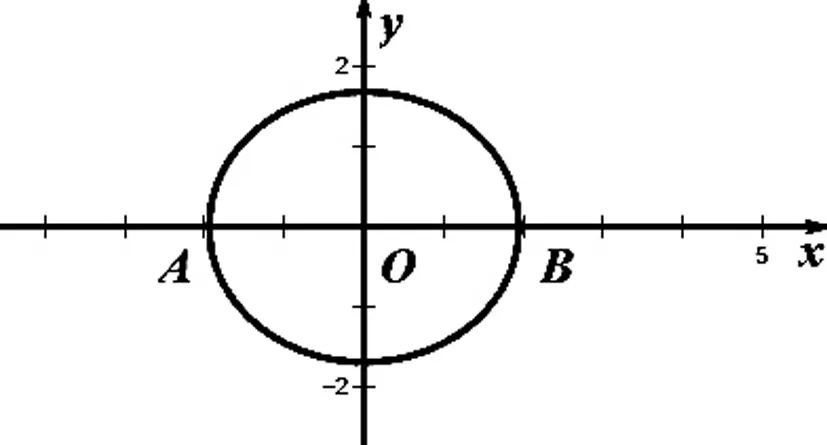
图1

(1)求椭圆C的方程；

(2)过点M(1,0)作一条斜率不为0的直线交椭圆于P，Q两点，连接AP、BQ，直线AP与BQ交于点N，探求点N是否在一条定直线上，若在，求出该直线方程；若不在，请说明理由.

这是我校高二期中考试模拟试卷的压轴题，满分12分，其中第(1)问4分，第(2)问8分.本题的年级均分不足4分，属于难题.接下来，分三方面进行探索与思考.

一、就题论题

教学时可设置如下的问题串：①你打算怎么解决这个问题？②解决这个问题分哪几步？引导学生用流程图的形式表示整个过程，建立框架，这也是解决问题的基本套路，下面提供三种解法.

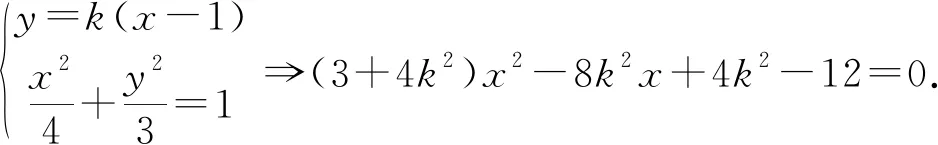
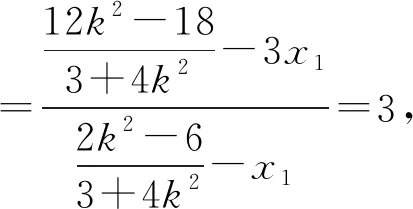
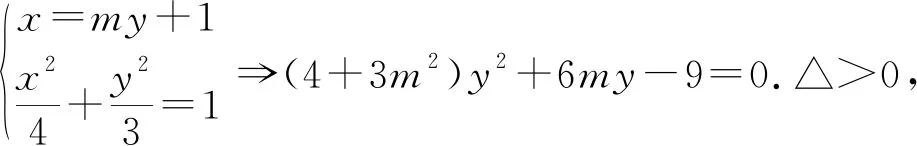
点评：三种解法都是用方程来研究问题，，最终都化为非对称式的处理，只是在细节处理上有所区别.法1更体现了通性通法，上手容易，但需要学生具备较强的计算能力和计算的勇气，这是解析几何教学时要关注和培养的；法2通过目标意识的指引，简化了法1的运算过程，先猜后证也是探索性问题教学时的常用策略，应渗透给学生；法3通过变换方程形式，大大简化了联立以后的方程及中间的运算，而且借助韦达定理巧妙地把积式化为和式，整体代入直接得出了最终结果，犹如神来之笔，这一经验值得积累.以后遇到非对称式，不妨借鉴一下，或许会有意想不到的效果.

二、推广探究

波利亚说过，解题就像采蘑菇一样，采到一颗蘑菇以后应四处看看，可能还会有别的收获.一般化是一种常见而且重要的数学思维方式，是获得数学命题的重要途径.本题中，注意到点M(1,0)是椭圆的右焦点，点N所在的定直线是椭圆的右准线，这是偶然还是必然？经过一番探究，笔者成功地将其推广到一般情形，得到了如下命题：

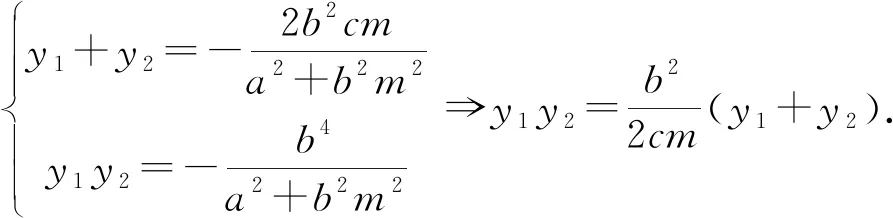
联立AP，BQ的直线方程并将上式代入得

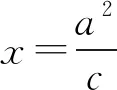
三、变式拓展

一个好问题就犹如一只会下金蛋的鸡，笔者据此提供了下列三个问题，供进一步思考：

教师研究解题，既可以模拟数学家的思维，从一般化、变式等方面展开；又可以从学生角度思考，预设卡壳点，设计活动去突破.只有这样，教师解题和解题教学才可以更好地联系起来，促进教师素养和学生能力的提升.