盘活三角知识 传播数学文化
湖北省襄阳市第一中学 (441000) 王 勇 吴玉红
数学文化是贯穿整个高中数学的重要内容,在高考中,以数学文化为命题背景的试题立意深远、构思精巧、内涵丰富,既能考查数学知识、能力、思想和方法,又能加深对中外数学文明的了解,增强爱国主义情怀,提高数学文化素养,丰厚数学文化底蕴.融入对数学文化的考查已成为新一轮高考命题改革的一个显著特征.下面精选以三角知识为依托的数学文化题六例并分类解析,旨在探索题型规律,揭示解题方法.
一、三角变换 精彩纷呈

图1
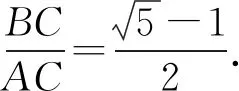

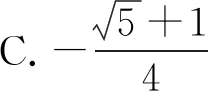
分析:求解本题的关键是弄清所求角与36°角,72°角及144°角之间的关系,再利用二倍角公式及诱导公式即可顺利求解.
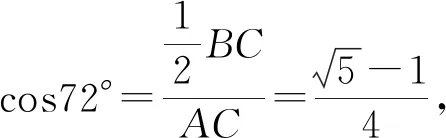
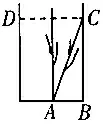
图2

A.①③ B.①③④ C.①④ D.②③④

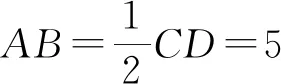
二、定理公式 运用自如

图3
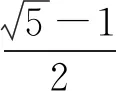
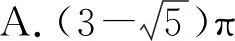
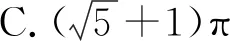
分析:利用数学文化“折扇”为背景命制的与三角函数相结合的题目,把雅致秀气的折扇与扇形的面积相交汇,体现了美育的素养导向.求解的突破口是熟记扇形的面积公式,把半径相同的两扇形的面积比转化为两扇形的圆心角的比,再利用它们的圆心角的和为2π,即可得小扇形的圆心角的弧度数.

例4 (2020·江西省十校联考题)阿波罗尼奥斯是古希腊数学家,他与阿基米德、欧几里得被称为亚历山大前期三大数学家,以他名字命名的阿波罗尼斯圆是指平面内到两定点距离的比值为定值λ(λ>0,且λ≠1)的动点的轨迹.已知在△ABC中,角A,B,C所对的边分别为a,b,c,且sinA=2sinB,acosB+bcosA=2,则△ABC面积的最大值为( ).
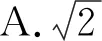
分析:根据正弦定理得a=2b,及余弦定理得c=2,建立适当的平面直角坐标系,借助阿波罗尼斯圆可得边AB上的高的最大值,进而求出△ABC面积的最大值.
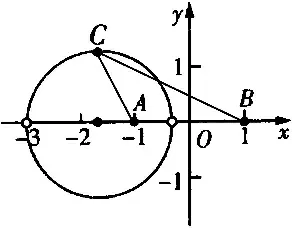
图4
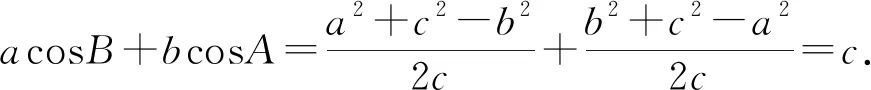
三、三斜求积 璀璨明珠
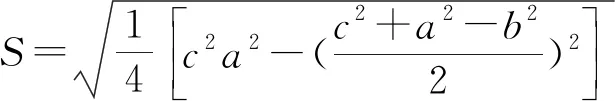
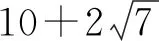
B.△ABC的三个内角A,C,B成等差数列
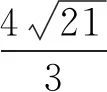



四、实际应用 三角发威
例6(2020·福建省质检题)上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图5①),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图5②为骨笛测量“春(秋)分” “夏(冬)至”的示意图.图5③是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.
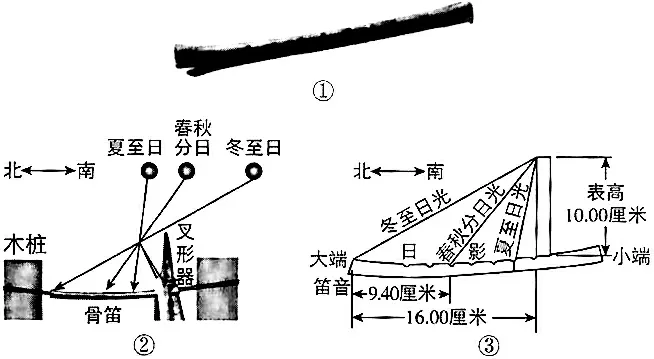
图5
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
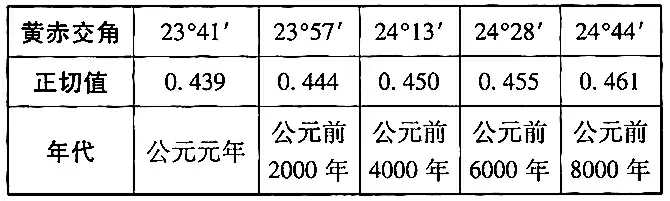
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ).
A.公元前2000年到公元元年
B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年
D.早于公元前6000年
分析:读懂题意画出示意图,通过解直角三角形和两角差的正切公式,计算出黄赤交角的正切值,对照题中的表格而得解.
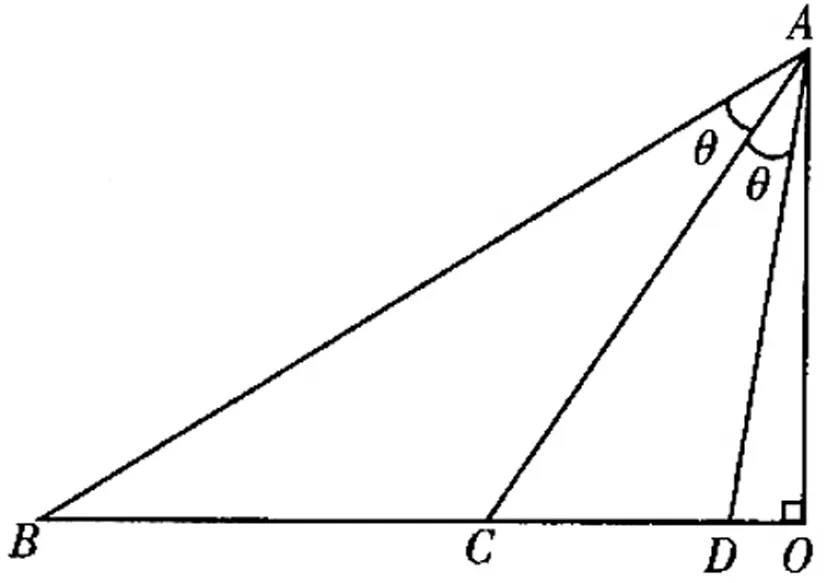
图6
解析:由题意可画出示意图,如图6,其中AO⊥BO(BO代表骨笛),AO=10.00,BC=9.40,BO=16.00,故OC=6.60.设黄赤交角为θ,由题意得
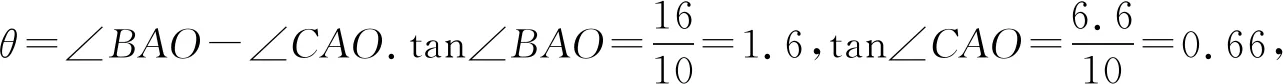
纵观以上各例,我们发现,此类数学文化题一般是从中外优秀传统文化中挖掘素材,将数学文化与三角知识有机结合,要求考生对试题所提供的数学文化信息材料进行整理和分析,在试题营造的数学文化氛围中,感受数学的思维方式,体验数学的理性精神.
———《扇形的认识》教学廖

