探源拓思融会贯通
———《扇形的认识》教学廖
廖国宝
【教学内容】
人教版六年级上册75、76页。
【教学准备】
教师:多媒体课件、练习纸等。
学生:圆纸片、量角器、彩色笔、练习本等。
【教学过程】
一、引:引生入境,唤起经验
1.欣赏扇形,唤起生活经验。
师:除了正方形、长方形、梯形、平行四边形和圆形,生活中还有一种图形我们经常见到。
课件出示:

师:这些美丽的图形,你们认识吗?(板书:扇形的认识)
师:学习新知识之前,同学们会问自己哪些问题呢?
生:扇形是怎样的图形?
生:为什么要学扇形?
生:扇形可以解决什么问题?
师:下面我们将一一探讨你们提出的问题。
2.闭眼画扇型,唤起潜认知。
师:闭上眼睛,想一想,扇形是怎样的?请大家用手在空中画一画。
二、探:寻根问源,一探究竟
1.从哪里来:扇形的产生,感知扇形与圆的联系。
师:你刚才画的扇形是哪种?
(根据学生的描述,课件先后顺序出示如下图形)
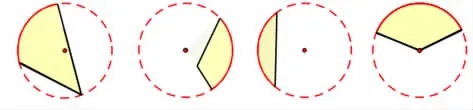
师:什么样的图形是扇形呢?
(课件动画演示生活中切披萨的情境,如下图)
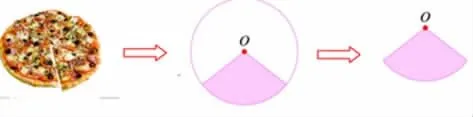
师:这样切出的披萨就是一个扇形。
(板书:圆的一条弧和经过这条弧两端的两条半径所围成的图形是扇形)
2.与什么相关联:扇形的认识,探究扇形与所在圆的联系。
探究活动:
(1)画一画。
师:动手画一个扇形,你会怎么画?
生:先画一个圆,再从圆心画两条半径,取其中一个扇形。
(2)想一想,议一议。
分组讨论:扇形与所在圆有什么联系?
师:看着你画的扇形,跟同学讨论一下:扇形跟什么图形有联系?它们有什么联系?有什么不同?
生:扇形和圆有联系
生:扇形的顶点是圆心。
生:扇形的弧是圆的一部分。
生:扇形的两条直边是圆的半径。
生:扇形有一个角和两条半径。
多媒体课件演示:扇形从圆中分离,闪烁扇形的两条边和顶点。
师:这两条边叫什么?顶点呢?下面我们认识一下扇形的各部分名称。
3.是什么:认识扇形的各部分名称和特征。
(1)认识扇形的各部分名称。
① 请学生带着问题自主阅读教材75页(如图)。课件展示问题:扇形有哪几部分名称?
师:你有哪些不明白的?把重点和不明白的地方用笔标示出来。
② 质疑、学生交流汇报。

微课展示:圆上取两点A、B中间那段曲线叫做弧,读作“弧AB”。课件闪烁“弧”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,即涂色部分。微课闪烁“扇形”。
像∠AOB这样顶点在圆心的角叫做圆心角。微课闪烁“圆心角”。
③ 基本练习。
练习一:动手做扇形。
师:刚刚我们认识了扇形,你想不想自己做一个?拿出课前准备的圆纸片,动手做一做。
(学生或折或剪或画,介绍扇形的各部分名称)
练习二:下面图形中哪些角是圆心角?在( )里画“√”。
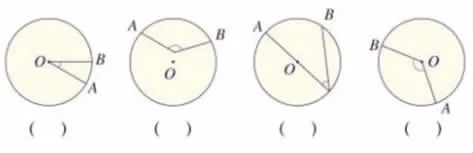
第一层次:为什么第二个图和第三图中的角不是圆心角?
生:因为这两个圆心角的顶点不在圆心。
第二层次:白板将图中的“弧”进行变化,圆心角的顶点在圆心,两条边是圆的半径,那么这是扇形吗?

明确:扇形存在于一个圆中,对应的圆、对应圆心角的弧只有一条。
(2)探索扇形的特征。
① 探索扇形的大小:扇形的大小跟什么有关?
第一层次:同一个圆。

猜测:从同一个圆形披萨切下两个不同大小的扇形披萨。你认为哪个大?
小结:同一个圆内的两个扇形,圆心角大的扇形就大。
第二层次:不同圆。
师:圆心角一样的扇形就一样大,对吗?
师:这两个扇形哪个大?
生:一样大,不一样大……
师:所以刚刚说的“圆心角大的扇形就大”,有个前提条件是“在同一个圆内”的两个扇形。(板书:在同一个圆内,圆心角大的扇形就大)
② 探索特殊扇形的圆心角。

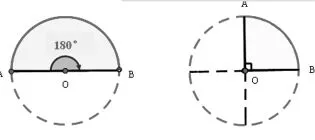
师:这是我们经常看到两种扇形。以半圆为弧的扇形,圆心角是多少呢?为什么呢?
生:是180°。因为扇形的两条边在同一条直线上,与顶点一起形成一个平角。
生:圆是 360°,半个圆的圆心角就是一半,180°。
师:以四分之一圆为弧的扇形的圆心角又是多少呢?
生:90°。因为以四分之一圆为弧的扇形圆心角是刚才以半圆为弧的扇形的一半,圆心角是90°。
在图上用圆规验证猜测。


小结:以半圆为弧的扇形圆心角是180°,以四分之一圆为弧的扇形圆心角是90°。
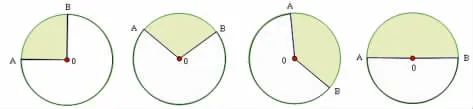
练习:量一量,下面扇形的圆心角是多少度?
三、拓:引导拓展,贯通前后
1.一个圆的面积是22m2,那么左图扇形的面积是( )m2;右图扇形的面积是( )m2。
2.画一画、涂一涂:一个圆的面积如果是“1”,请画一画,涂上颜色表示面积是、、的扇形。

3.拓展练习:你在生活中见过下面这些图案吗?

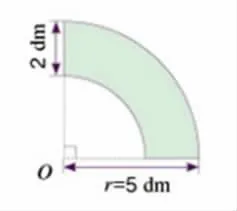
像下面这样把一个圆环截得的部分叫做扇环。你能求出下面扇环的面积吗?
四、全课总结
师:同学们,今天我们学了什么知识?是怎样学习新知识的?你有什么感受?

