《解决归总问题》教学设计

谢翔翔

【教学内容】

人教版三年级上册第72页。

【教学过程】

一、“变”中激趣，导“问题”

1.引入“线段图”。

（1）课件出示：

师：同学们，老师今天带来了一条会变魔术的线。（课件演示）

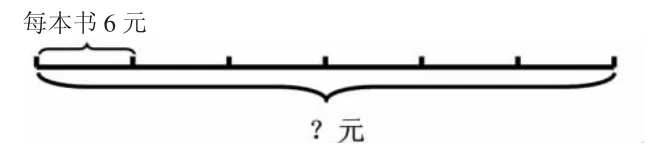
问：你知道了什么信息，“？”表示什么意思？

呈现：买6元一本的书，正好可以买6本，一共要多少钱？

学生独立尝试列式并解答：6×6=36（元）。

追问：为什么用乘法？

（2）

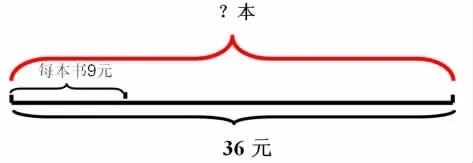
师：你又知道了什么信息？

呈现：每本书9元，一共36元，可以买几本？

学生独立尝试列式并解答：36÷9=4（本）。

追问：说一说，为什么用除法？

小结：数学上常常会将信息和问题藏在这样的线段中，这样就组成了一幅线段图。

2.合并信息——引题。

（1）将上面两个信息合并成一道题。

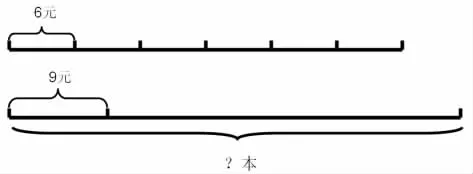
呈现：老师的钱买6元一本的书，正好买6本，用这些钱买9元一本的书，可以买几本？

（2）画图表征，尝试解题。

要求：

①画：用画线段图或其他图来表示题目中的信息和问题，并尝试列式解答。

②想：想一想，先算什么，再算什么？

【设计意图：在画图表征环节，线段图的呈现是学习的瓶颈。选择以“变”中导“图”的形式引出线段图，以解读数量关系为主，将知识点由易到难地呈现。先“扶”着学生理解线段图，明确每部分的意义，再尝试“放手”，让学生用画线段图或其他图来表示题目中的信息和问题，体现“循序渐进”的教学原则，培养学生的画图表征技能。】

二、“比”中感知，解“问题”

1.呈现表征作品。

（1）

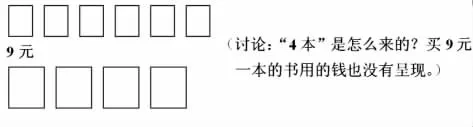
（讨论：“4本”是怎么来的？买9元一本的书用的钱也没有呈现）

（2）

（3）

（4）

2.对比感知。

图（2）：引导观察，是否表示出了题目中的信息问题。明确要想表示出所有信息，必须要画2条线段。

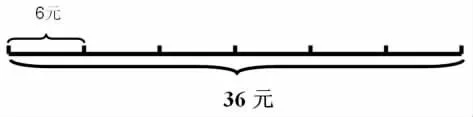
图（3）：引导学生观察，从图中获得了什么信息？重点在于理解9元一本的书所在的线段表示的意思。

将图（3）与（4）进行比较。

询问：这两幅图，哪幅图更准确些？

交流：买6元一本的书与买9元一本的书所用的钱相等，可是题目中并没有告诉我们，从哪里知道的？

小结：在线段图中可以用相等的线段表示相等的量。

3.自我检验。

请将自己的线段图改成正确的样子。

【设计意图：本环节以对比为主线，在反复比较中层层递进，不断凸显出线段图的本质，引导学生关注“用这些钱”，初步感知题目的中间问题。】

4.理解算理。

（1）读懂线段图后，算式怎样列呢？

［6×6=36（元），36÷9=4（本）；6×6÷9=4（本）］

（2）思考：解题时先求什么，再求什么？和你的同桌说一说。

（3）讨论：为什么要先求出买6本6元的书一共用了多少钱？

（4）明确：只有求出了买6本6元的书一共用了多少钱，才能求出9元一本的书可以买几本。这是本题的中间问题。

（5）反思：解决问题时先干什么，再干什么？

（6）检验：4本9元的书和6本6元的书用的钱是一样的，解题正确。

【设计意图：授人以鱼更要授人以渔。在算式的依托下引发思考，解题时先求什么再求什么，为什么要先求6本6元的书的钱。不断追问、讨论、反思，学生头脑中初步建立“先求出中间问题——总价钱”的模型。再通过检验，经历问题解决的全过程，让学生的解题和分析能力得到提升。】

三、“练”中求思，用“问题”

1.建立模型。

这次展览虽然以“2018 中国·南亚东南亚国际美术展(雕塑)”为名，但根据参展艺术家的情况，展览的作品并不局限于中国、南亚和东南亚诸国，也有英国、意大利、保加利亚等欧洲国家的艺术家参与，从而形成了一种生发于云南昆明，架构在亚洲和欧洲板块上的国际艺术交流活动。参展的雕塑作品中有的抽象或具象，有的变形或写实，无论是从形的塑造、材质运用还是从表现主题等层面来看，参展作品的差异性构建了展览的多样性，多样性中又包含着艺术家的个性和生活认知，也包含着雕塑家所属国家的现实与历史文化，从而形成以艺术形态所呈现的异国文化的碰撞与交融。

（1）完善表格：9与？填哪里，为什么？

师：根据每本书的价钱乘书的数量，我们可以求出（总价钱）。

问：能在表格中找到36吗？

（2）变式。

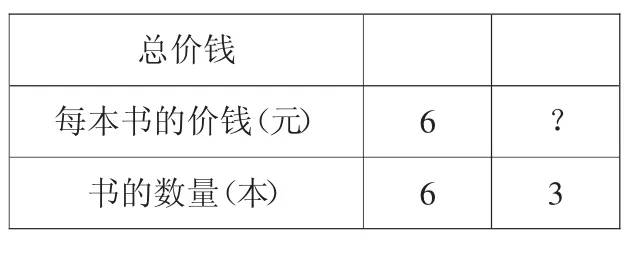
引导说一说表格中3和？的意思。6×6÷3（先求什么，再求什么）。

沟通联系：这些算式有什么相同点？（都是先算6×6，并顺势框出）

（3）变与不变。

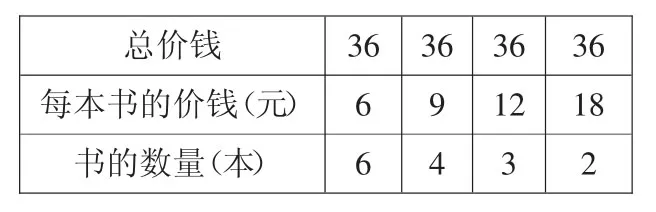
小结：不管求每本书的价钱，还是求书的数量，我们都是先用乘法求总价钱，再用除法解题。像这种先求总数的问题，在数学上叫做“归总问题”。

【设计意图：本环节以表格的形式表征问题，丰富学生的表象。通过变式，引导学生观察什么在变，什么不变，渗透函数思想与变与不变的思想，建立数学模型。】

2.看图列式

（1）小华读一本书。

①

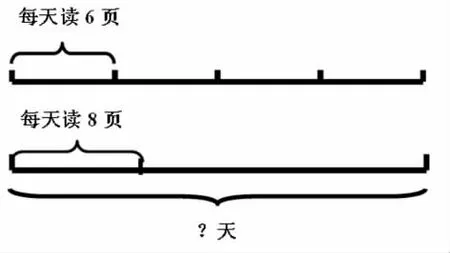
②

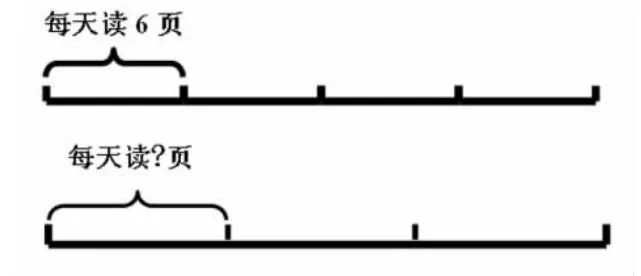
思考：这两幅线段图向我们传递了什么数学信息？

解题：任选一题，尝试列式。

（2）对比。

比一比：这两题有什么相同点和不同点？

相同点：都是先算6×4，也就是先求出“这本书一共有几页”。

不同点：问题不同，一个求几天读完，一个求每天读几页。

小结：无论是求份数，还是求每份数，都要先求出总数。

（3）变式。

（隐去单位，只留下问号）

延伸：这两条线段图除了表示读书的问题，还可以表示其他什么数学问题？请任选一幅线段图，编一道数学问题。

反馈：请学生说题，其他同学听，他编的是哪一幅线段图？

（4）打破定势。

①有一批零件，工人叔叔每小时做8个，2小时做完。如果每小时做4个零件，需要几小时做完？

②工人叔叔2小时做了8个零件，照这样计算，4小时做几个零件？

师：比一比，这两道题有什么不同？

（一个先求零件总数，一个先求每小时的零件个数）

【设计意图：本环节安排看图列式，实现由半编题到编题的过渡，通过归一问题与归总问题的对比，打破思维定势，让学生思维更上一个层面。】

四、“思”中升华，忆“问题”

师：静静地思考，这节课你有什么收获？我们是怎样学习的？

师：如果有机会，你还想学习什么知识？

【设计意图：对课堂学习进行回顾，既梳理了知识形成的脉络，又对学习方式做了小结。对课堂学习进行延伸，激发学生应用所学知识和方法进一步探究学习的欲望。】