利用问题链导向深度学习的设计与实施

☉上海市青浦区豫才中学 孟甚晖

深度学习是将个人内在的对学习的需要作为动力，通过理解帮助学习，学习者有能力对新的内容进行批判性的学习，并将新内容与原有知识进行联系，具有将原有的知识在新的情境中运用的能力［1］.

基于问题链教学的初中数学深度学习是基于知识的内在结构和整体特征，以问题为主线，以知识为载体，引导学生从知识学习走向思维发展，从低阶思维走向高阶思维［2］.问题链的设计与完善，有助于理清整节课的主线“脉络”，其清晰的条理性使学生更易于理解，有助于学生“平滑”地接受新知识.本文以笔者所上公开课“弧长”及几次磨课为例，通过课堂中的三个活动，从改善概念教学、优化公式推导、突破难题难点三个角度，围绕问题链的设计意图与实施效果，谈谈利用问题链导向深度学习的实践与思考.

1 教学实例

活动1：利用问题链改善概念教学

（1）问题链设计，如图1.

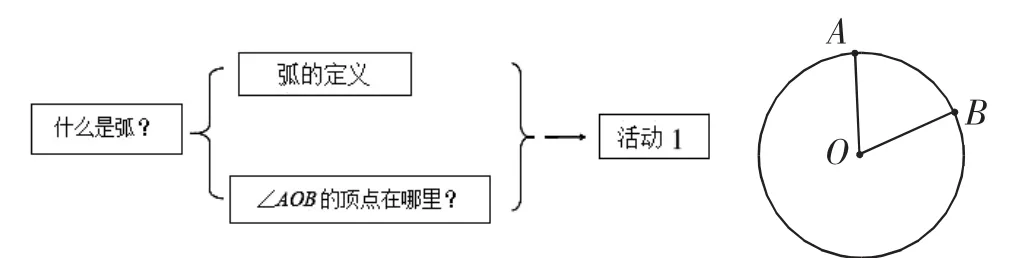
图1

设计意图：本节课内容是弧，活动1主要是对弧及圆心角的概念教学.通过提问一个具体圆心角∠AOB的顶点位置，直观理解圆心角的意义，为后面判断圆心角提供理论依据.

（2）课堂实践.

在试讲时，学生利用课前学习单自主学习知识点.由于缺乏系统的讲解与引导，导致学生概念模糊.正式上课时，笔者取消了课前预习单，而是通过提问引入概念.

师：已知半径OA，如果我在圆上再取一点B，连接OB，得到了一个什么？

生：∠AOB.

师：这个角的顶点在哪里？

生：圆心.

师：顶点在圆心的角，我们称为圆心角.这个圆心角在圆上截取了一部分，A、B两点之间的部分我们称它为弧.

……

活动2：利用问题链优化公式推导

（1）学习单设计.

问题1：观察：弧的长度与什么因素有关？

当半径不变时，弧的长度与______有关；当圆心角不变时，弧的长度与________有关.

问题2：在同一圆中，半径为r：图中（图略）圆心角∠AOB各是几度？圆心角∠AOB所对弧长分别是圆周长的几分之几？

问题3：能说出下列各圆心角所对的弧长是圆周长的几分之几吗？会求弧长吗？

72°的圆心角所对的弧长是圆周长的________，弧长为________；48°的圆心角所对的弧长是圆周长的________，弧长为________；135°的圆心角所对的弧长是圆周长的________，弧长为________；1°的圆心角所对的弧长是圆周长的________，弧长为________；n°的圆心角所对的弧长是圆周长的________，弧长为________.

弧的长度l与圆心角n、半径r有什么关系？能否用一个数量关系表示？

问题4：归纳弧长公式：l=________.

（2）问题链设计，如图2.

图2

设计意图：活动2是本节的重点，即推导弧长公式.这里利用部分与整体的关系：先从角度入手，理清圆心角与周角的关系，从而得出弧长与圆周长的关系，进而推导出弧长公式.

（3）课堂实践.

这部分经历多次修改，学生从“圆心角是周角的几分之几”到“弧长是圆周长的几分之几”，容易出现理解上的“断裂”，导致无法顺利推导出公式.

（4）课后反思.

问题2（改）：表1图中所示各圆心角占这个圆周角的几分之几？圆心角所对弧长分别是圆周长的几分之几？

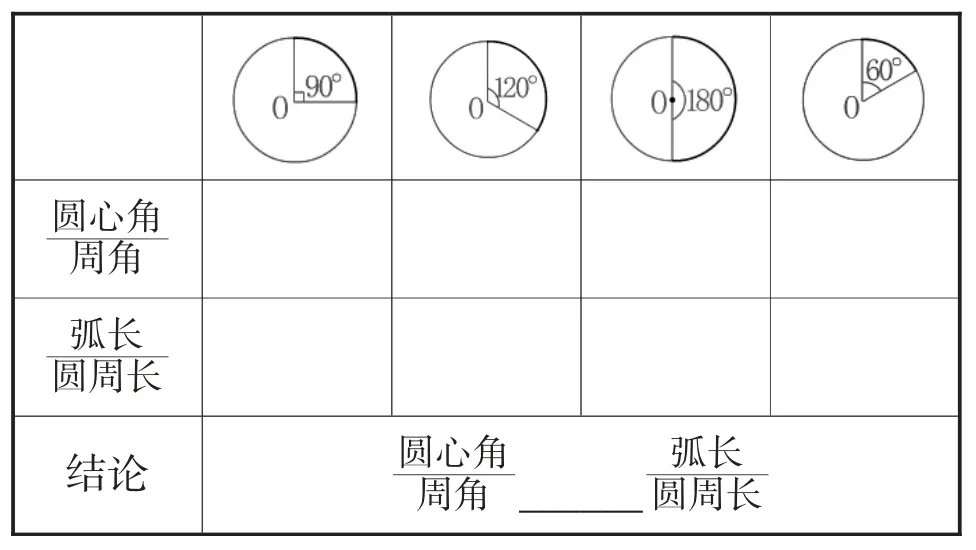
表1

问题3（改）：下列各圆心角所对的弧长是圆周长的几分之几？

72°的圆心角所对的弧长是圆周长的________，1°的圆心角所对的弧长是圆周长的________，n°的圆心角所对的弧长是圆周长的________.

活动3：利用问题链突破难题、难点

（1）学习单设计.

例题1：如果圆的半径长r是1厘米，求180°的圆心角所对的弧长l.

练习1：如果圆的半径长r是40厘米，弧所对的圆心角为36度，求弧长.

练习2：三角形ABC的三条边长都是30毫米，分别以

例题2：圆的半径长为5厘米，一个圆心角所对的弧长为6.28厘米，求这个圆心角的度数.（π取3.14）

练习3：已知一条弧长为6.28厘米，弧所对的圆心角为90度，则这条弧所在圆的半径多少？（π取3.14）

（2）问题链设计，如图3.

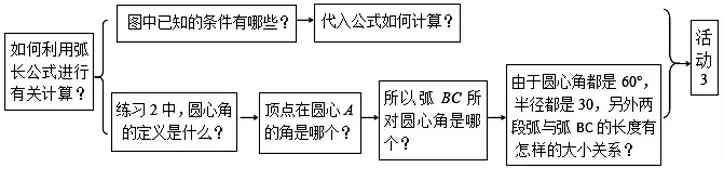
图3

设计意图：活动3是弧长公式的运用，通过问题链梳理解题的一般步骤：列出已知条件，代入公式，解方程.练习2是本节的难点：在复杂图形中寻找弧所对的圆心角.因此问题链从回顾圆心角的定义入手，寻找圆心角及相应的半径，再分析三条弧长之间的大小关系，最后利用一般步骤解决.

（3）课堂实践.

【评注】练习2的问题链经历了一次修改，修改前的试讲片段如下：

师：三条边的长相等，因此三个角相等，内角和为180度，每个角都是60°.

师：你会画弧吗？我们一起看黑板：以点A为圆心、27毫米为半径的是哪段？

师：我们得到了弧BC，它所对的圆心角是哪个角？

生：∠A.

师：圆心角和半径分别都知道了，我们代入公式.那弧AC呢？弧BC呢？

……

【评注】通过修改问题链，使条理更加流畅、清晰，更易于学生理解.

黑板上演示画弧BC.

师：还记得圆心角的定义吗？

生：顶点在圆心的角.

师：顶点在圆心A的角是哪个？

生：∠A.

师：所以弧BC所对的圆心角就是哪个角？

生：∠A.

师：由于三个圆心角∠A=∠B=∠C=60°，半径都是30毫米，因此弧AC、弧BC、弧AB的长度有怎样的大小关系？

生：相等.

师：所以求出弧BC以后，只要怎样即可？

生：乘以3.

……

2 结语

借助问题链的设计，不仅能改善概念教学，利用问题思考帮助学生突破难点，还能加强指导，有效启发，让学生在循序渐进中理解知识，逐步掌握知识的发生、发展过程，最大限度地提高课堂学习质量.问题链也可以看作教学设计的一条主线：如实际授课效果不如预期，只需优化相应的问题链即可，既提高了教师备课的操作性，又有助于把握整节课的节奏.问题链中每个精心设计的小问题，都是导向深度学习的“指路牌”.