“一图一课”：聚焦经典几何图形的变式教学——兼谈中考几何复习的教学建议

☉江苏省无锡江阴市周庄中学 缪瑞华

很多学校在中考几何复习时，往往是一轮复习重复着学生在新授课期间所学内容的知识点、图形性质或判定的梳理，并链接着讲评各地中考几何题；二轮复习则将题型各异的几何题分类复习，如几何动态问题、几何开放题、几何新定义题、几何分类讨论题，等等.以上几何复习课的课型划分看似分门别类、面面俱到，但是有一个不足，就是往往在一些归类复习时，选的几何题“形同而质异”，学生在这些几何习题的题海中训练之后，对一些经典几何图形问题的变式再练容易出现“似曾相识，仍需要长时间思考”，结果考试时间不够，造成解题障碍.笔者近年针对一些经典几何图形问题开展“一图一课”研究，取得较好的教学效果.下面以一个经典几何图形问题为例，概述教学流程和设计意图，最后浅谈中考几何复习的一些思考与建议，与同行们研讨.

1 经典几何问题“一图一课”教学流程

教学环节1：从一个经典几何问题出发

经典几何问题：如图1，正方形ABCD中，点E是边AB的中点，点P在边BC上，且，连接DE、PE、DP，求证：△PDE是直角三角形.

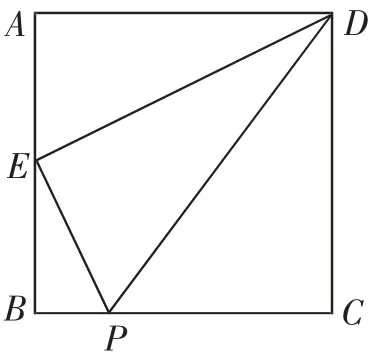
图1

说明：该题在不同版本的初中教材中都出现过，在八年级学习勾股定理的逆定理之后就可练习，在九年级学习相似之后有不同的证法.

教学组织：开课阶段，先安排学生思考这道题的不同证法，然后小组内交流，再全班汇报展示.通过交流活动，可以让学生对这个经典几何问题的不同解法进行复习与回顾，为后续变式问题提供必要的解法铺垫.

教学环节2：变式研究

变式题组：如图2，正方形ABCD的边长为4，点E在边AB上，PE⊥DE交BC于点P，点Q在线段DE上，且EQ=AE.

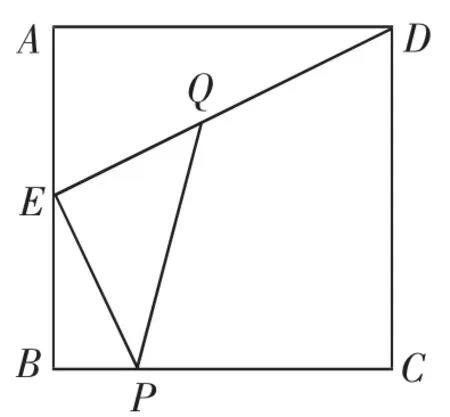
图2

（1）当AE=BE时，求四边形BPQE的周长.

（2）当点E运动时，四边形BPQE的周长是否为定值？若是定值，请求出该定值；若不是定值，请说明理由.

变式意图：第（1）问比较容易，可分别求出EQ=AE=2，BE=2，利用△ADE△BEP，可得BP=1，.在Rt△PEQ中，PQ=3.从而四边形BPQE的周长为8.

第（2）问有一定的难度，预设以下一些不同的思路.

思路1：（基于“计算”的思路）设AE=4x（注意，这里的设元比较“特殊”，主要是方便后续运算过程中一些系数都是整数），则BE=4-4x，EQ=4x.由△ADE△BEP，可得BP=x（4-4x），PC=4-x（4-4x）.利用勾股定理表示PQ2=EP2+EQ2，PE2=BE2+BP2，将含x的式子分别代入，计算、配方出PQ2=16［1-x（1-x）］2.又PC=4-x（4-4x），可得PC2=PQ2，即PC=PQ.于是四边形BPQE的周长可转化为AB+BC=8.

思路2：（基于“证明”的思路）如图3，连接PD.在Rt△PED中，PD2=EP2+ED2.在Rt △PCD 中，PD2=CP2+CD2.于是EP2+ED2=CP2+CD2，则CP2=EP2+ED2-CD2.由边长AD=CD，可得CP2=EP2+ED2-AD2.又在Rt△AED中，AE2=ED2-AD2，所以CP2=EP2+AE2.又AE=EQ，则CP2=EP2+EQ2.而在Rt△PEQ中，PQ2=EP2+EQ2.于是PQ=PC.思路接通，四边形BPQE的周长为定值.

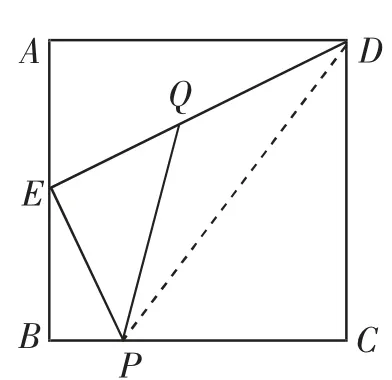
图3

教学组织：由于第（2）问比较难，所以需要给学生“较长的时间”（课堂上至少给10分钟）思考，然后安排小组交流、全班展示.如果还有困难，教师可以给出一些“提示语”，比如，设AE=x，然后分别计算PQ、PC的长（用含x的式子表示）.教学之后，还可给出一个变式拓展问题.

拓展问题：如图4，正方形ABCD的边长为a，点E在边AB上，连接DE，作PE⊥DE，交BC于点P，在DE上取一点Q，使EQ＝AE，连接PQ.随着点E在边AB上的不同位置，求PQ的最小值.

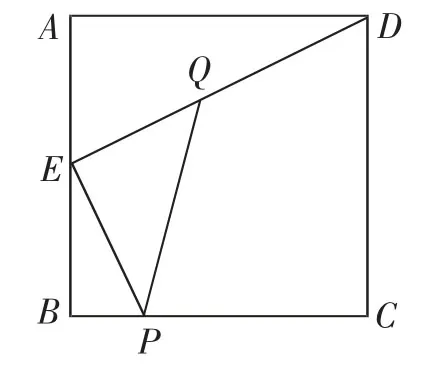
图4

设计意图：上面变式问题中的第（2）问已经研究了周长不变的性质，关键是证出PQ＝PC，拓展问题可以将PQ转化为PC，而PC的最小值对应着BP取得最大值.于是可设AE＝4x，则BE＝4-4x，EQ＝4x.由△ADE△BEP，可得BP＝x（4-4x）.根据二次函数的最值分析法，求出PB的最大值为1，相应的PC的最小值为3，即PQ的最小值也为3.

教学环节3：课堂小结，布置作业

小结问题1：本课关注的这道以正方形为背景的几何综合题学习过程中，你觉得解题过程中哪些关键步骤让你印象深刻？先思考一下，然后小组内交流，每个小组再选派一名代表上台讲解.

小结问题2：学习本课之后，你还想到了哪些以正方形为背景的几何综合题求解或证明的思路与本课中的类似？小组内先交流后再全班汇报分享.

作业设计：如图5，正方形ABCD的边长为2021，点E在边AB上，连接DE，作FE⊥DE，交BC于点F，在DE上取一点G，使EG＝AE，连接FG.若BF＋FG＝t，求t的值.

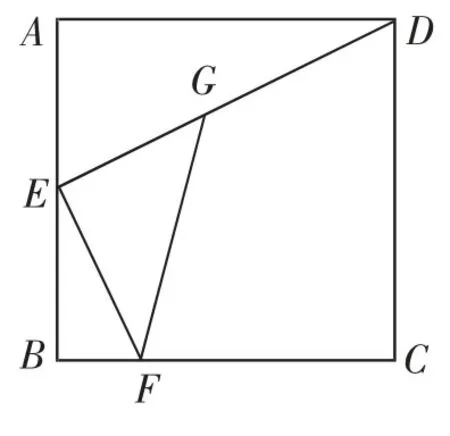
图5

设计意图：解题的关键是证明FG＝FC，从而可以将BF＋FG转化为BF＋FC＝BC＝2021.

2 中考几何复习的教学建议

2.1 重视经典问题，挖掘课本上的好题素材

教材是数学家、数学教学研究人员、数学教材编写人员的集体智慧，不但数学概念的表述、呈现方式是精心设计的，围绕一个数学概念或性质的习题编拟也是精心设计的，值得广大一线教师深入研读.在“用好教材”的理念指引下，要十分重视教材上一些经典问题的教学功能.以上文中的经典问题为例，不只是组织学生得出这道题的具体解法，还要认识到这类问题的重要性，这类问题在不同年级、不同章节中的多角度思考，而且可以围绕这类问题开发出一些专题课例，加深学生对这类问题的解题运用.从这个意义上说，挖掘教材上的好题素材，应该成为一线教师的专业基本功之一.特别是，识别课本上的好题，需要教师对本地中考试卷有较全面、细致、深入的研究，这样遇到类似好题时，就能联系到教材上的一些经典例、习题，有利于进一步的备课、预设和变式再练.

2.2 加强变式教学，组织学生踊跃展示

顾泠沅先生及其团队长期研究变式教学，成为我国中学数学教学的一个重要特色.很多经验丰富的教师多善于开展变式教学研究.对习题教学研究来说，开展变式研究是更加重要的教研追求.以上面课例中提及的这个经典问题为例，注重开展变式研究，可以让学生在复习阶段减少机械刷题的“无趣”，能享受到探索一道旧题的新结论的愉悦感.在组织开展经典问题的变式教学时，教师可先安排复习学生在新授课阶段曾经学习过的一些经典问题，这个环节类似于“旧知引入”，然后有序进行变式研究，变式问题出示之后，要留出时间让学生先独立思考，然后小组讨论、全班展示.缺少独立思考的小组讨论是虚假的，多数学生在小组讨论时容易成为“观众”而不是“思维参与者”.

2.3 适时拓展提升，训练学生高阶思维

作为中考复习课的教学目标之一，围绕几何问题的拓展提升也是复习课的重要追求.每份中考试卷的最后两道大题中，都会安排一道几何综合题，这些几何综合题一般都有2～3个小问，其中最后一问都是拓展提升问题，承载着一份试卷的区分选拔功能.中考复习备考时，需要我们针对一些几何经典问题进行必要的生长拓展，帮助学生深刻理解这些经典问题，训练学生的高阶思维，同时提升几何综合题的解题能力，特别是让学生看出一些较难题也是由以前熟悉的经典问题“一步一步”生长拓展出来的.

3 写在后面

中考复习课的研究一直是非常重要的教研课题，如何让“刷题式”的解题教学成为充满探索味儿的复习课，是很多教师努力追求的复习目标.本文基于经典几何问题的变式拓展教学，可以看成一种课例研究的努力，我们的课例实践还不够丰富，认识也不全面，期待更多同行的课例研究，让中考复习课的研究走向深入，共同提升复习课的教学品质.