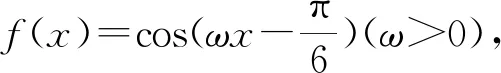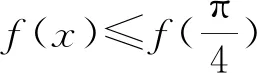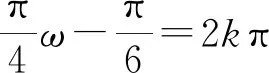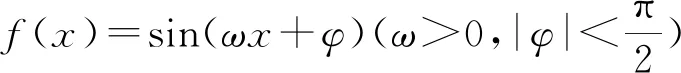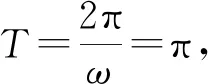抓住三角函数的“五性”速解题

江苏省金湖中学 (211600) 张太清

在许多与三角函数相关的问题中，如果我们能够挖掘三角函数中蕴藏的周期性、奇偶性、单调性、对称性和有界性并有效使用，从而就抓住问题实质、使问题的快速解决，起到事半功倍的作用.下面通过几个典型题例，展示这些性质的精妙运用给解题带来的效果，供读者朋友参考.

一、周期性

若对函数y=f(x)，存在实数T≠0，使等式f(x)=f(x+T)对任意x都成立，则称此函数为周期函数，T为一个周期.

例1 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ≤π)一个周期内图像的最高点是(2,2)，与它相邻的最低点的横坐标是6，则f(1)+f(2)+f(3)+…+f(2020)=.

评注：求一些函数式若干项的和的问题，找出其式子规律性(如周期性)是非常重要的思维趋向.

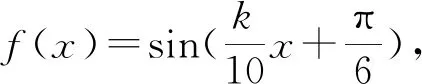
评注：抓住所给周期的范围就是抓住了问题的关键点，为后面快速解题铺平了道路.

二、奇偶性

若函数y=f(x)，若对定义域内的任意x都有f(-x)=f(x)，则称函数f(x)为偶函数；若对定义域内的任意x都有f(-x)=-f(x)，则称函数f(x)为奇函数.

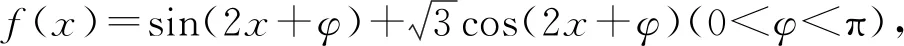
评注：对于一般的三角函数式，若需判断函数的奇偶性、单调性或求函数的最大值和最小值等问题时，首要任务是将其转化为f(x)=Asin(ωx+φ)的形式，然后再根据条件求解.

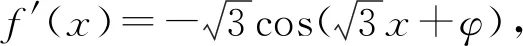
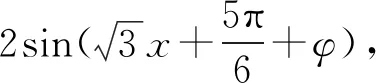
评注：此题是三角函数与导数的综合题，体现了高考题的考查目标与方向，抓住三角函数为奇函数的特点解决参数求值问题是破题的关键.

三、对称性

对于函数y=f(x)，若在定义域内任意x，都有f(a-x)=f(a+x)成立，则称此函数关于直线x=a对称；若都有f(a-x)=-f(a+x)成立，则称此函数关于点(a,0)对称，其中偶函数与奇函数是这两种情况下在a=0时的特例.

评注：由于三角函数y=sinx的对称轴是比较熟悉的，所以这里判断出所给函数是轴对称问题就是解题的重要环节.

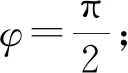
评注：将中心对称的条件转化为一个等式，再分析化简这个等式，求出待求参数的值是解决此类题最基本的思路.

四、单调性

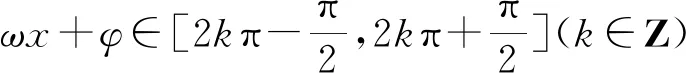
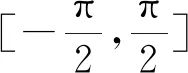
评注：已知函数的单调区间求其它问题，就是将已给的区间看成是整个函数区间的子集，然后建立等式或不等式解决问题.

五、有界性

如果函数y=f(x)对给出的区间上任意x都满足f(x)≤M，则称M是此函数的上确界，满足f(x)≥N，则称N是此函数的下确界.