初中数学文化与数学思想方法教学摭例

陈瑜清

[摘  要] 在初中数学教学中，教学的内容除了数学知识之外，还有两个非常重要的范畴，这就是数学文化与数学思想方法. 对于初中学生而言，理解数学文化与数学思想方法的重要性，可以从这样几个方面进行：一是数学文化与数学思想方法可以让学生更好地认识数学学科;二是数学文化与数学思想方法可以让学生更好地建构数学知识;三是数学文化与数学思想方法可以让学生更好地运用数学知识. 初中数学教师要通过自己的教学理解与教学智慧，在课堂上种下数学文化与数学思想方法之种子，然后提供给学生学习土壤，那么数学文化与数学思想方法就能够落地生根，开花结果.

[关键词] 初中数学;数学文化;数学思想方法

在初中数学教学中，教学的内容除了数学知识之外，还有两个非常重要的范畴，这就是数学文化与数学思想方法. 通常情况下，对数学思想方法的认识常常是：在数学知識建构过程中具有一定规律性的思想和方法就是数学思想方法. 而数学文化则有所不同，数学文化看起来是一个空洞的概念，但实际上在数学发展的过程中，数学文化往往才是起着决定性作用的因素. 数学文化既是数学发展过程中沉淀下来的，同时又推动着数学学科沿着正确的轨道发展. 从初中数学教学的角度来看，数学文化与数学思想方法对学生的学习都起着重要的作用. 相比较而言，数学思想方法与数学知识的关系更为接近，在数学知识学习与运用的过程中，更容易理解数学思想方法的作用. 一般认为，数学思想方法对数学教学有着重要的促进和指导作用，它不仅是学生形成良好认知结构的纽带，还是由知识转化为能力的桥梁，是培养学生数学意识、形成优良思维素质的关键，因此我们要加强数学思想方法教学的意识并在数学教学过程中不断地挖掘和渗透;再看数学文化，如果学生在数学知识学习的过程中，能够感受到数学文化的存在，又或者运用数学文化的思路促进自己更好地建构数学知识，那么这样的初中数学教学，就能够展现出更好的样态，即使从数学学科核心素养培育的角度来看，也可以开辟更新颖的途径.

初中数学文化与数学思想方法

教学的重要性

在初中数学教学中渗透数学文化以及数学思想方法无疑是有意义的. 一个很重要的原因就在于，数学文化可以滋润学生的数学学习过程，而数学思想方法则可以让学生在数学知识学习与运用的过程中感受到数学学科的规律性. 事实证明，初中阶段的学生在理科知识的学习过程中，都有寻找规律的原始动力. 如果寻找到规律，那么他们就会感觉知识的学习变得更加简单. 数学思想方法原本就是人们对数学知识和方法形成的规律性的理性认识、基本看法;数学思想方法就是解决数学问题的根本策略和程序，是数学思想的具体化反映. 对于初中学生而言，理解数学文化与数学思想方法的重要性，可以从这样几个方面进行：

一是数学文化与数学思想方法可以让学生更好地认识数学学科. 大量的教学经验表明，相当一部分初中学生认为数学学习就是无穷无尽地计算，尽管数学学科核心素养中有数学运算的要求，但必须认识到计算并不是数学学习的全部，相当一部分重要的数学概念的形成，背后都有着深刻的文化因素. 在这些数学概念或者规律的学习过程中，如果能够渗透数学文化与数学思想方法，就可以化解数学学科的抽象性，从而让学生感觉到数学学科是有趣的，数学学习的过程是有趣的.

二是数学文化与数学思想方法可以让学生更好地建构数学知识. 数学知识的学习，越来越被认为具有建构性. 当学生在自己的学习基础或者生活经验上生成新的数学概念或者规律时，如果能够伴随着数学文化或者数学思想方法，那么学生在认识这些数学知识的时候，就能够更好地认识到这些数学知识存在的意义以及形成的逻辑，在运用的时候也更能够将这些数学知识与具体的问题情境结合在一起，从而寻找到更适合自己的数学知识建构途径.

三是数学文化与数学思想方法可以让学生更好地运用数学知识. 上面提到数学知识的运用，这实际上是一个学以致用的关系，要想让学生认识到数学知识的运用不只是重复地计算，必须借助数学文化和数学思想方法，将数学知识与数学文化、数学思想方法结合在一起，数学知识的运用才具有魂，学生才能充分感受到数学学习及其运用的意义.

初中数学文化与数学思想方法

教学实践例析

在以上三点认识的基础之上，初中数学教师必须在教学实践中不断地寻找数学文化与数学思想方法的渗透途径. 从宏观方面来看，教师在数学教学中必须树立全新的观念，在教学中体现数学的文化价值，增强数学的人文性，并注重培养学生的创新能力，帮助学生树立正确的数学观;除此之外，还必须认真发掘数学知识中的思想方法元素，真正将数学知识与数学思想方法结合在一起，通过这种结合与融合，才能真正实现数学文化与数学思想方法的渗透. 从这里来看相应的教学案例：

案例1  在“一元一次方程”的教学中，笔者注意到传统的教学能够让学生感觉到，就是利用方程解决问题可以变得更加方便，除此之外更多的是学生在重复解题中的厌烦. 而事实上，方程在数学史中有个重要的内涵，因此在方程这一知识的教学中，教师可以向学生渗透一些数学发展史. 比如说，向学生介绍大约在3600年前古埃及人在问题解决的过程中，就已经运用到了含有未知数的等式;而在公元820年前后，在中亚、西亚曾经出现了专门关于方程解法的著作;到17世纪时，著名数学家与哲学家笛卡尔最先提出用x，y，z来表示未知数. 于是方程的形式也就真正形成了……这样一个社会发展的过程，一方面可以让学生认识到方程的由来，另一方面也可以让学生更好地认识到方程的内涵及其在数学问题解决中的作用.

这实际上就是一个借助数学发展史，渗透数学文化的过程. 这样的数学文化渗透可以让学生认识到方程知识实际上是有血有肉的，是可以在实际生活中解决问题的. 在得到这一认识之后，方程在学生心目中的地位就会有所不同，这种认识是传统教学无法达到的.

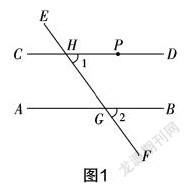
案例2  “平行线的判定”的教学. 在这一内容的教学中，最重要的数学思想方法之一就是逻辑推理. 学生在学习的过程中，面对“同一平面的两条直线平行”这一问题，学生的第一反应是根据平行线的定义进行判断，但是平行线的定义中“永不相交”是无法判定的，因为直线无限延伸，除此之外，只能借助逻辑推理去进行. 这个逻辑推理过程又是建立在数学抽象基础之上的，此处所设计的可供数学抽象运用的情境是：运用直尺和三角尺画平行线. 对于学生而言，这首先是一个操作的过程，从判定法则运用的角度来看，则是一个抽象后的推理过程，学生首先要做的是将三角板沿着直尺平移，抽象成如图1所示的图形.

有了这一抽象结果之后，逻辑推理的方向也就明确了. 例如，如果两条直线被第三条直线所截，假设同位角相等，那么这两条直线是否平行？在问题的驱动之下，逻辑推理可以顺利发生，平行线的判定法则也就容易演绎出来.

这就是一个蕴含的数学抽象、逻辑推理等数学思想方法的过程，通过这样的过程，学生可以认识到数学知识的得来必须遵循一定的逻辑，从而强化对逻辑的认识，这也就是对数学思想方法的认识.

初中数学文化与数学思想方法

教学之思

在上面的教学例子当中，数学文化与数学思想方法的渗透过程都是自然发生的. 当然这得益于有针对性的教学设计，特别值得强调的就是，当教师带着明确的数学文化与数学思想方法渗透的意识进行教学时，展现在学生面前的就有可能是一个达到预期教学目标的教学过程. 也就是说，初中数学教师要通过自己的教学理解与教学智慧，在课堂上种下数学文化与数学思想方法之种子，然后提供给学生学习土壤，那么数学文化与数学思想方法就能够落地生根，开花结果.

综上所述，数学思想是人类思想文化宝库中的瑰宝，是数学的精髓，它对数学教学具有决定性的指导意义. 在核心素養的背景之下，在初中数学教学的过程中，就是应当渗透数学思想方法，如方程思想、分类讨论思想、数形结合思想、整体思想、化归思想等多种数学思想方法;又或者通过数学史的介绍，渗透数学文化的情境，这样就可以培养学生的思维能力，从而提高学生的学习效果. 这既是初中数学知识教学的需要，也是数学学科核心素养培育的需要，满足了这些需要，就能够让学生在数学知识的建构与运用过程中，达成数学文化与数学思想方法的融合.

3611501908255