探索几何类比，生成破题方法

杨卫兵

[摘  要] 几何类比探究题的解析思路较为特殊，需要通过知识迁移、模型方法类比来突破，同时该类问题可按照一定的解题流程进行剖析，逐步从图形分析过渡到类比构建思路. 文章将以一道几何类比探究题为例，探究解析过程，总结破题策略，并开展教学反思，提出相应的教学建议，与读者进行交流.

[关键词] 类比;几何;探究;特殊模型;策略

类比探究题常出现在中考几何压轴题的位置，试题形式通常为分环节设问，且一般设置三小问. 第一环节以发现问题、证明问题为主，第二环节围绕“类比”进行知识探究，第三环节侧重知识的应用与拓展. 其中类比探究是问题考查的核心，涉及模型类比、方法类比和知识类比，解析时要充分把握“问题发现与证明”环节的核心特征，注意总结归纳.

几何类比探究题所探究的内容较为多样，包括常见的数学模型、线段与角度的求解方法等，常涉及数形结合、分类讨论、化归转化等思想方法，解析过程要关注“变化”中的“不变”，充分利用特殊模型的结论来简化过程.

关于实例问题的思路分析

【证明推断】 如图1所示，已知四边形ABCD为正方形，点E和Q分别是BC和AB边上的点，DQ⊥AE，垂足为O，点G和F分别位于CD和AB上，GF⊥AE.

①试求证DQ=AE;

②推导的值.

【类比探究】 如图2所示，在矩形ABCD中，设=k（k为常数）. 现将矩形ABCD沿着GF折叠，使点A恰好落在BC边上的点E处，可得四边形FEPG，设EP与CD相交于点H，连接AE与GF，设交点为O. 试探究GF与AE之间的数量关系，并写明理由;

【拓展应用】

在上述“类比探究”条件成立的情况下，连接CP，当k=时，有tan∠CGP=，GF=2，试求CP的长.

解析：环节一为“证明推断”，以正方形为背景，融合了双垂直关系，需要关注线段关系的推导过程.

①证明：由正方形的性质可得AB=DA，∠ABE=∠DAQ=90°，则有∠QAO+∠OAD=90°，由题可推知∠ADO+∠OAD=90°，于是可得∠QAO=∠ADO，所以△ABE≌△DAQ（ASA），由全等性质可证DQ=AE.

②该问推导线段的比例关系，由DQ⊥AE和GF⊥AE可证DQ∥GF，结合FQ∥DG可证四边形DQFG是平行四边形，由其性质可得FG=DQ. 又知AE=DQ，所以FG=AE，从而可得=1.

环节二为“类比探究”，该环节对矩形进行了折叠，四边形为普通的矩形，探究GF与AE之间的数量关系，可以类比环节一中几何模型的解析方法，逐步突破. 对于其中的线段关系，可以借助全等或相似性质来构建.

过点G作AB的垂线，设垂足为M，如图3所示. 通过角度推导可得∠BAE=∠MGF，从而可证△ABE∽△GMF，所以=. 因为∠AMG=∠D=∠DAM=90°，所以四边形AMGD为矩形，则有GM=AD，所以===k，即=k.

环节三为“拓展探究”，需要对上述环节进行总结归纳，显然模型的核心解法是推演其中的三角形全等或相似关系，利用模型的性质来推导线段之间的长度关系.

可过点P作BC延长线上的垂线，设垂足为M，如图4所示. 根据其中的平行关系可得∠CGP=∠BFE，所以tan∠CGP=tan∠BFE=. 可设BE=3a，BF=4a，则EF=AF=5a. 因为=，GF=2，可得AE=3. 在Rt△ABE中使用勾股定理可解得a=1，则BE=3，AB=9. 根据比例关系可得BC=6，进一步得到BE=CE=3，AD=PE=BC=6. 通过角度推导可证△FBE∽△EMP，由相似性质可得==，代入线段长有==，可解得EM=，PM=，所以CM=EM-EC=，由勾股定理可得PC==.

关于解题策略的深入分析

上述是关于几何模型及解法的类比探究题，以矩形为背景，类比了三角形相似模型的推断方法以及线段关系的轉化思路，问题的解题策略有着一定的参考价值. 下面以上述问题为例进行解题思路的概括.

1. 解题过程中的“四招”突破

类比探究题的解析过程可概括为找特征、探思路、提模型、照搬抄，具体内容如下.

（1）找特征，关注模型中的特殊角、特殊图形、特殊点以及几何折叠和旋转等过程.

如本题中AE分别与DQ，FG为垂直关系，四边形ABCD为正方形，矩形折叠后点A和E关于直线FG对称，则点O为线段AE的中点. 同时存在等角，故可利用其中的等角、等边关系构建相似或全等三角形.

（2）探思路，借助类比探究环节之间的联系，从特殊到一般，总结问题的解析方法，探究问题的突破思路.

如上述问题，“证明推断”环节以正方形为背景，推断证明线段关系可通过提取其中的全等模型，利用模型性质来完成. 故“类比探究”环节虽然给出的是一般的矩形，但依然可以采用此思路，利用余角关系推导等角关系，提取其中的相似模型，利用相似性质完成线段关系的推导.

（3）提模型，提取图像中的几何模型，利用模型性质进行几何推导.

几何综合题的图像一般较为复杂，但图像中往往隐含了一些特殊的几何模型，充分利用模型的结论可简化解析过程. 以上述问题为例，利用全等三角形的性质求等线段的长，利用相似模型求线段之间的比例关系，利用直角模型的勾股定理求线段的长等.

（4）照搬抄，即照搬前一环节解析问题的方法和思路来解决后一环节的问题，包括辅助线的作法、图像中的模型、条件转化推导的思路等.

上述类比探究题的核心是几何模型，包括其中的直角模型、全等模型和相似模型，第二环节作辅助线后直接构建了三角形相似模型，后续利用模型的性质即可完成线段关系的推导.

2. 几何探究题中常见的模型

特殊模型是击破类比探究题的利器，提取图像中的模型有助于解题思路的构建，因此在解题探究中要注重模型的总结积累. 下面以常用的旋转模型为例进行深入讲解.

（1）“A”字形（手拉手）旋转模型

手拉手模型在几何探究中十分常见，该模型结构中存在有公共顶点的两个三角形，且有等线段或等比例线段关系，连接对应顶点后可形成“手拉手”的模式，从动态角度可将两个三角形视为是旋转关系，构建了旋转模型，如图5、图6所示.

（2）“K”字形旋转模型

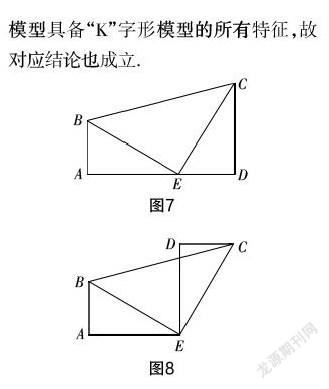
“K”字形旋转模型的核心是垂直，即该模型中存在三个直角，也称“三垂直”模型. 该模型在角度和线段和之间存在着显著的关联. 若以其中一个顶点进行翻折，则可生成相应的“K”字形旋转模型，如图7、图8所示. 实际上该旋转模型具备“K”字形模型的所有特征，故对应结论也成立.

关于类比探究题的教学反思

几何类比探究题是初中数学的经典问题，问题的知识跨度大，综合性强，命题立意也较为高远，所涉分问题的关联递进特征显著. 上述对该类问题进行了实例探究与方法总结，对于拓展学生的解题思维有着一定的帮助，下面结合教学实践进行思考.

1. 重视读图，总结思考

求解几何类比探究题的关键步骤是读图审题，通常需要在第一环节对问题中的图像特征有着充分的了解，找到突破图像解析的关键，并在此基础上进行深入思考，总结解析的思路，对问题中的关键条件、图形的每一个特征，都要有深刻的理解. 图像解析的思路往往是后续类比的关键，因而解题探究时要注意总结解图的方法思路，尤其要注意图像中的模型特征. 教学中教师要引导学生掌握读图的基本思路、构图技巧以及图像探究的方向，提升学生的审题能力.

2. 注重类比，知识迁移

“类比”是几何类比探究题的核心，该类问题的构思极为巧妙，主要考查学生的类比迁移能力，问题往往由简单的模型、结论作为起点，逐步深入，形成复合模型，但解决问题的核心方法、思想、思路是相一致的，依然是对基本概念、结论、模型的衍生拓展，因此发现和类比使用其中的性质是突破问题的关键. 在教学中，教师要强化学生的知识基础，引导学生关注知识关联、掌握类比的方法技巧，培养学生的知识迁移能力，激发学生的创新思维.

3. 归纳模型，形成策略

几何类比探究题的形式多变，类型多样. 解题探究時将重点放在对题型的划分、模型的归纳和方法的总结上，以引导学生形成解题策略为教学的核心任务. 以上述类比探究题为例，在完成实例探究后笔者和学生一起深入反思了考题，总结了问题突破的“四招”以及常用的几何模型，后续学生解题时可充分利用该策略来构建思路. 教学中教师可指导学生对类型题进行对比分析，提炼解析方法，形成具体、系统的解题策略，以提升学生的核心素养为最终目标.

3561501908255