关于对角互补四边形模型的探究与思考

施德仪

[摘  要] 对角互补四边形模型是初中重要的几何模型，该模型总体上可分为两大类型，即90°的对角互补模型和120°的对角互补模型. 利用模型特性可推得关于角平分、线段关系和几何面积等的一些结论以及模型中的四个顶点共圆. 文章将深入解读模型，结合实例应用模型，并对模型进行拓展探究，从而提出相应的教学建议.

[关键词] 对角互补;四边形;模型;旋转;四点共圆

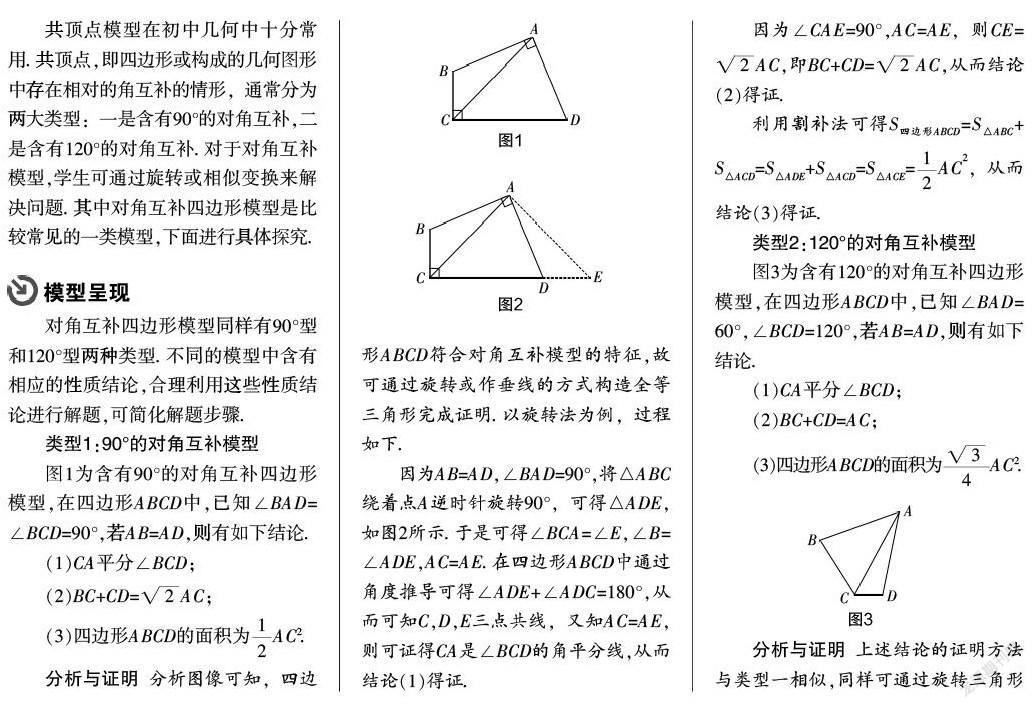
共顶点模型在初中几何中十分常用. 共顶点，即四边形或构成的几何图形中存在相对的角互补的情形，通常分为两大类型：一是含有90°的对角互补，二是含有120°的对角互补. 对于对角互补模型，学生可通过旋转或相似变换来解决问题. 其中对角互补四边形模型是比较常见的一类模型，下面进行具体探究.

模型呈现

对角互补四边形模型同样有90°型和120°型两种类型. 不同的模型中含有相应的性质结论，合理利用这些性质结论进行解题，可简化解题步骤.

分析：由图像可知，四边形CDEF为对角互补四边形，由其性质可知，四点位于同一圆上，故可作其外接圆，借助圆周角定理来推导相关的角度条件.

解：矩形ABCD中，已知∠BAE=∠CDE=90°，AB=CD，又知BE⊥AC，则C，D，E，F四点均在以CE为直径的圆上，故可作出该圆，如图11所示，可推知∠CED=∠CFD. 利用条件可证△ABE≌△DCE，所以∠DEC=∠AEB，利用角度推导可得∠AEB=∠DCF=∠DEC=∠DFC，所以DF=DC.

评析  对角互补四边形的顶点共圆是该模型的显著特征，模型中隐含了圆的几何性质，充分利用圆周角定理可推导相关角度的大小. 解题时可以按照“提炼模型→构建辅助圆→圆性质推导”的思路进行建模和解析.

解后反思

1. 深入探究模型，研读模型性质

对角互补四边形模型在初中几何中十分重要，有着极高的研究价值，探究过程要关注模型的知识背景，总结模型的解析策略及性质特征. 对角互补四边形模型中融合了角平分线、垂直平分线、几何旋转，其中隐含了角平分线的性质定理、垂直平分线的性质定理以及三角形全等等知识. 在探究过程中，教师要引导学生借助全等来推导角和边长的关系. 教学中建议采用“模型解读→性质总结→应用强化”的思路逐步探究模型，认识模型的性质，完成从“知识认知”到“知识应用”的过渡.

2. 倡导模型拓展，循序引导教学

开展模型探究要遵循循序渐进、由浅入深的原则，同时注重模型拓展. 以上述对角互补四边形模型为例，教学中除了要注重模型的基本特征、性质讲解外，还应合理地拓展模型，如四边形的四点共圆，可增设一些铺垫式的问题，引出四边形的隐圆，合理设问引导学生进行思考. 另外，还可在圆的知识背景中讲解四点共圆的性质，或是基于几何旋转来看待模型中的全等关系. 教学中教师要关注学生的思维活动，及時启发学生进行思考，充分引导学生构造模型、转化条件，激发学生的思维，使学生充分掌握模型.

总之，对角互补四边形模型的应用价值极高，学生在探究过程中需切换视角全面剖析，可从几何旋转、三角形全等、四点共圆等角度深入解读，关注模型的解析思路，理解模型的性质特征，掌握模型的应用策略，形成分析模型的解题习惯.

3266501908251