加强师生互动，优化数学教学

张波

[摘  要] 文章认为加强师生互动，优化课堂教学可从营造良好的互动环境，创设开放的教学情境，引导学生积极参与这三方面做起. 以一道等腰三角形的试题为例，具体阐述在课堂教学中师生如何进行有效互动，促使课堂动态生成.

[关键词] 师生互动;课堂;等腰三角形

崔允淳教授提出：教育者应从关注课堂教学的“教”与“学”逐渐走向关注课堂的“何以学会”. 学生知识和技能的获得与课堂中知识自我建构有着显著的联系. 数学课堂从本质上来看，就是师生、生生之间双边互动、情智共同发展的过程. 简而言之，初中数学的学习是个体自主建构与多向合作的过程，学生在互生互长的课堂中更好地建构知识结构，发展自身的主体能力.

课堂中的有效互动是指师生、生生之间或群体间进行多层面、多形式、多程度的交互影响，这种影响主要表现在双方情智与心灵的层面上，互动双方得到共同进步与发展的教学行为. 這也意味着教师需在课堂氛围、情境创设与师生互动等方面狠下功夫，使得师生在课堂中保持心灵开放、共同参与、智慧互通等.

促进师生互动的基本措施

1. 营造良好的互动环境

课堂是师生践行互动的主要阵地，新课标引领下的初中数学课堂已然摒弃了传统的师生主客体的关系. 当今的数学课堂是师生双边交互、对话的模式，一般以“主—客—主”的形式呈现，其中师生之间是“主与主”的关系，而教学内容则是中间的“客体”，具有为两个主体铺路搭桥的作用.

和谐、平等、共享、宽容的教学环境能有效地激活多重主体之间的关系，促进教学互动的有效性. 良好的教学氛围可让师生双方获得愉悦、灵动与畅达的教学体验，从而悦纳彼此，信任并尊重对方，形成师生情智互动的良好环境.

2. 创设开放性的教学情境

教学是行动、解释、领悟与创造的过程，师生是教学活动的行动者，其互动过程直接影响着教学的成效. 优质的数学课堂犹如一场盛大的交响乐，必须由各种具有独特性的声调融合在一起才能组合成令人回味无穷的天籁之音. 因此，教学中除却教材提供的教学素材之外，教师应引导学生从不同渠道搜集相关资料，以拓宽学生的视野，为教学活动提供更多的信息源.

创设开放性的教学情境，能让学生在丰富的信息环境中接收到更多的感官刺激，从而敏锐地捕捉到利于学习的资源，为生态课堂的生成奠定一定的基础.

3. 鼓励学生积极参与

每个存在的生命都是丰盈、主动、进取的，当下，初中学生更具独特的个性特征. 而张扬学生的个性，则是新课标对我们提出的要求. 因此，教师应引导学生主动地参与到教学活动中来，激发学生的生命力量，使他们获得新的学习体验，使得课堂具有生机与活力.

为了激发学生参与教学的积极性，教师要对一些勇于挑战、善于提问、敢于质疑的学生给予更多的鼓励与赞扬;而对一些学习积极性不高，缺乏独立思考能力或不敢表达自己的学生应给予更多的关注与关爱，可从他们的最近发展区着手，以强化他们主动参与的意识.

案例分析

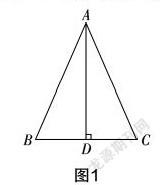
原题：如图1，已知在△ABC中AD⊥BC，点D为垂足，且AB+BD=AC+DC，求证：△ABC为等腰三角形.

师：这是上一节课结束留给大家思考的一道题，现在来说说你们的想法？

生1：此题给了两个条件，我是先考虑AB+BD=AC+DC这个条件的. 本题无法直接算出结果，但AB，BD这两条线段与AC，CD都不在一条直线上，我就考虑能否将它们放到一条直线上来进行思考. 为此，就想到分别延长AB，AC，在它们的延长线上截取与BD，CD长度相等的线段.

师：这个想法不错，哪位同学来说说具体的解题过程？

方法一：

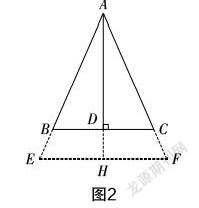
生2：如图2，将AB、AC分别延长到点E与点F，使得BD=BE，CD=CF，再连接EF，延长AD与EF交于点H，可得AE=AF，则△AEF为等腰三角形，接下来就不会了.

师：分析得很好！但是，在此基础上怎样将问题与AD⊥BC这个条件相结合，证明△ABC是一个等腰三角形呢？

（学生讨论，无果）

师：既然这个思路行不通，那我们尝试换一个角度来思考.

生3：先前的思路是将BD和DC分别添加在AB，AC的延长线上，那我们能否将AB，AC转化到与BD，DC同一根直线上呢？

师：这个想法有点道理，我们再来试试看.

方法二：

生4：将DB延长到点M，使得BM=AB，同样将DC延长到点N，使得CN=AC. 分别连接AM，AN，可得MD=ND，因为AD⊥BC，所以△AMN为等腰三角形，由此可知∠M=∠N. 因为BM=AB，NC=AC，所以∠M=∠BAM，∠N=∠CAN，因此∠ABD=∠M+∠BAM=2∠M，∠ACD=∠N+∠CAN=2∠N，所以∠ABD=∠ACD，所以AB=AC，△ABC为一个等腰三角形.

师：很好，以上两种思路看起来差别不大，却决定了能否解决问题. 因此，我们在遇到解题障碍时，不要钻牛角尖，而要学会换一个视角去看待问题，试图从其他途径解决问题. 针对本题，如果不添加辅助线，有没有办法利用AD⊥BC这个条件寻找解题的突破口？

生5：根据直角三角形的性质，应该能解决本题.

师：很好！来说说你的想法.

方法三：

生5：根据勾股定理可得AD2=AB2-BD2，AD2=AC2-CD2，分别计算可得（AB+BD）（AB-BD）=（AC+CD）（AC-CD），所以AB+BD=AC+CD①，AB-BD=AC-CD②，由①+②可得2AB=2AC，所以AB=AC，因此△ABC为一个等腰三角形.

分析：此题的教学过程中，师生之间通过良好的沟通与互动，共同探讨解题的方案. 当第一种方案失败时，学生在教师的引导下，换一种思路继续尝试，发现将问题转化到同一条直线上时，则很快求得结果.

同时，在教师的点拨下，学生发现除了运用线段来解决此题的问题之外，还可以“AD⊥BC”这个条件为解题的突破口，在不作辅助线的基础上，运用勾股定理的性质亦可解决此题. 由此可见，解题技巧的获得源自不断尝试与思考. 正当笔者准备总结时，有位学生提出了新的问题. 这超出了笔者的课程预设，打乱了计划中的教学节奏.

生6：若将条件中的AB+BD=AC+DC改为AB-BD=AC-DC，本题还能证明△ABC是一个等腰三角形吗？

虽然这是教师预设之外的问题，但这确实是一个值得探究的问题，从中也能看出学生学习的积极性. 为此，笔者决定沿着学生的思路继续往下探究，以满足学生对知识的渴求，同时也表现出对学生的尊重与肯定，使得教学达到触类旁通的效果.

探究一：

师：在之前解题的基础上，我们来思考生6所提出的问题，哪位同学来说说你们的看法？

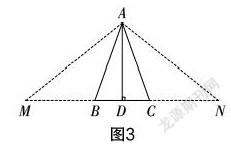
生7：如图4，延长BC到点K，延长CB到点L，使得AB=BK，AC=CL. （过程略）可证得△ABC是等腰三角形.

探究二：

师：若本题没有提供图形，那么图4有没有其他可能？

生8：有，在没有提供图形的基础上，点K、L有可能落在线段BC的内侧，也存在与点B、C重合的可能.

师：也就是说在不提供原題的情况下，存在着三种可能. 请一位同学总结一下这三种分类.

生9：①当点K与点L落在线段BC的外部时，BC

师：很完整. 也就是生7的解题中应附加一个AB>BC的条件. 还有两种类型，请大家参照生7的解题方法，自行完成.

分析：解题本就需要经历反复尝试的过程，虽然尝试了不一定能达到解决问题的目的，但不尝试是一定不会有新的发现的. 当遇到一种方法行不通时，可转换思维的角度，换一种思路去尝试，一旦找到解决问题的办法，再想方设法地优化这种解题方法. 在此过程中，师生之间积极互动很重要，教师可以适当地引导，以激活学生的思维. 因此，尝试是为我们积累解题经验的良好途径，也是让我们收获宝贵经验的手段.

探究三：

为了发展学生的解题能力，深化学生的解题技巧. 教师提出：能否把AD⊥BC这个条件改为其他条件？

生10：可将AD⊥BC这个条件换成“AD为∠CAB的角平分线”或“点D为BC边的中点”.

师：那我们就一个一个地来讨论.

……

本教学过程，教师首先营造了一个良好的教学氛围，学生在宽松、愉悦的环境中积极参与、主动思考，并提出各种假设试图解决问题. 当课程偏离预设轨道时，教师顺势根据学生的思维继续深入探究本题，让课堂变得更具生命力. 此过程有效地燃起了学生探究的热情，课堂因“意外”而获得的知识比预设的更好.

3439501908211