积累数学活动经验,发展直观想象
李俊


[摘 要] 数学起源于生活、来源于生活,文章探索在初中数学教学中通过折纸活动,引导学生在几何知识探究中,从直观观察到表象表征,再到抽象内化培养其直观想象能力,从而促进学生数学核心素养的提升.
[关键词] 数学活动;折纸;直观想象
《义务教育数学课程标准(2011年版)》指出:“数学活动经验的积累是提高学生数学素养的重要标志. ”“数学活动经验需要在‘做’的过程和‘思考’的过程中积淀,是在数学学习活动过程中逐步积累的. ”心理学家皮亚杰指出:“活动是认识的基础,智慧从动作开始.”直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养. 史宁中教授说过:“数学的思路是‘看’出来的,不是‘证’出来的. 这种‘看’的依赖就是数学直观. ”笔者认为,史教授所说的“看”,不仅仅是用眼睛看,动手操作也是一种观察体验,更有助于提升“看”的效果. 因此,利用数学活动课——动手探索操作,发展学生的直观想象,是非常直接、有效的方式. 下面以“折纸中的数学思考”教学为例,尝试在综合实践课程的活动中,培养学生的直观想象能力,发展学生的数学核心素养.
备课思考
备课思考的内容是新人教版八年级下册“平行四边形”一章的数学活动1——折纸做60°,30°,15°的角. 根据以往的数学活动的经验,本节课为了让学生从比较容易动手操作的环节开始,并能够通过操作而体会层层深入,揭示折叠的本质——轴对称. 笔者根据本章的矩形的性质,结合已经学习过的轴对称的性质和勾股定理的弦图,设计了“折纸中的数学思考”一课,通过折纸让学生建立对轴对称变化的直观认识,并通过轴对称的性质解决一些与边、角有关的几何问题,培养学生的空间想象能力,以及发现问题、分析问题和解决问题的能力.
教学实践
1. 问题初探,形成直观印象,揭示折叠的本质
探究活动1:利用矩形纸片折出等腰三角形. 分小组折一折,要求:(1)用直尺、虚线画出折痕. (2)用实线画出你折出的等腰三角形. 由此得到两种折叠方法:
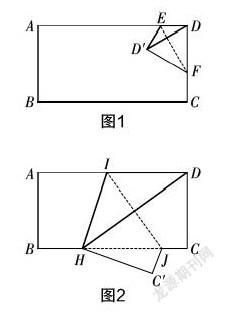
方法1:折矩形纸片的一个角. (如图1、图2所示)
原理:有两边相等的三角形是等腰三角形.
追问1:你还能找到其他相等的边、相等的角吗?
追问2:图1、图2中有哪些是二倍角的关系?
方法2:对折矩形纸片. (如图3所示)
原理:垂直平分线上的点到线段两个端点的距离相等.
追问3:当______=______时等腰三角形ABP是等边三角形.
如何折叠可以得到等边三角形?动手试一试.
设计意图 让学生初步感受折叠的本质是关于折痕的轴对称变化,折痕所在的直线就是对称轴,可以充当角平分线和垂直平分线的作用. 通过折叠得到全等的图形,从而得到对应线段和对应角相等,对应线段相等就可以得到等腰三角形. “追问1”和“追问2”进一步让学生在实践操作的过程中,探寻几何模型,形成几何直观. 寻找二倍角可以让学生对等腰三角形顶角的外角等于底角的两倍这个基本模型从折纸过程中抽离出来,建立几何直观印象. 这个活动既有动手操作,可以培养学生的折叠技能;又有一定的趣味性,还可以揭示折叠的本质和复习全等的知识. 提出“追问3”,为后面“探究活动2”的操作提供了思路,为问题再探做好了铺垫.
2. 问题再探,从表征到抽象,抽离几何模型
探究活动2:利用矩形纸片折特殊角.
操作1:在一张矩形纸片上,你怎么折出一个45°的角?
原理:平分矩形纸片的一个直角.
追问1:由45°的角,你还能折出哪些度数的角?
操作2:你能通过折纸的方法,折出一个30°的角吗?怎样折?
小组讨论:说出你們的方法并与大家分享.
方法:(1)对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;(2)再一次折叠纸片,使点B落在EF上交于点N,并使折痕经过点A,得到折痕AM,同时得到线段AN.(如图4、图5所示)
追问2:在图5中,你能找出所有的30°的角吗?60°的角呢?还有其他度数的角吗?还能折出15°的角吗?
设计意图 在学生揭示了折叠的本质以后,继续对特殊角的探究,既是对折叠本质的进一步巩固,也是对折叠基本模型的直观化或可视化. “操作1”的设计不但强化了学生对角平分线的认识——只要将角对折就可以平分角,而且直观地证明了角是轴对称图形——它的对称轴是角平分线所在的直线,也就是折痕所在的直线. “操作2”中结合了折一个等边三角形和平分60°角的方法,并且在整个图形中融合了等边三角形的“三线合一”和直角三角形“30°角所对的直角边等于斜边的一半”的模型.
上述活动利用矩形纸片的直角与直角边的特点,结合对直角三角形的已有认知,构建有特殊边、角的轴对称图形. 操作过程中纸片的变化具有很强的直观感,可以培养学生的空间想象能力、推理能力,让几何模型生动化.
课堂练习:如图6所示,将矩形ABCD沿EF折叠,使点B落在AD边上的点G处,点C落在点H处.
(1)通过折叠,四边形EBCF翻折到了四边形______的位置,对称轴是折痕______所在的直线,即四边形______≌四边形________. EB=________,BC=______=______,FC=______.∠BEF=∠______,∠EBC=∠______=______°,∠C=∠______=______°,∠EFC=∠______.
(2)若∠DGH=30°,连接BG,则∠AGB=______.
设计意图 通过折叠题目的练习,让学生从实践操作(动作表征)形成的关于轴对称图形的几何直观(表象表征)深入理解并过渡到符号性表象(符号表征). 如果说“问题(1)”直接引导学生发现了轴对称图形等边、等角的关系,那么“问题(2)”则是引导学生对轴对称图形等角关系的理解和应用,需要抽象出全等角、角平分线等关系,以此培养学生将几何模型从空间直观中抽离出来的能力.?摇
3. 拓展提升,从抽象到内化,固化几何模型
如图7所示,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5. 在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于 ?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你试一试用矩形纸片折出可能出现的情况.
设计意图 “问题(1)”:由折叠得到∠BMN=∠1,可以算出∠BMA的度数;由矩形对边平行得到内错角相等,即∠MKN=∠BMA,求得∠MKN的度数. “问题(2)”:由矩形对边平行得到内错角相等和折叠角相等,可以得到△MNK是一个等腰三角形;求△MNK的面积可以把KN看成底,则高恒为1. 若△MNK的底KN为1,则△MNK的面积刚好等于 ;但若KN=KM>1,则△MNK的面积一定大于 .“问题(2)”为“问题(3)”做铺垫,只要折叠以后使等腰三角形MNK的底边KN最大,这时面积就是最大. 通过折叠可以发现,若对折使点B与点D 重合,或者沿对角线AC 折叠时,等腰三角形MNK的面积最大.
对实验操作类题目的设置,利用“探究活动1”和“探究活动2”形象化的直观印象,并关联旧知,引导学生发现矩形纸片对边平行形成的内错角相等和折叠后得到的两个角相等,由此构造等腰三角形,然后抽象形成“平行线间的夹角平分得等腰三角形”的基本幾何模型解决实际问题,进一步让操作形成的直观想象内化.
4. 应用升华,玩转数学弦图,深化问题探究
探究活动3:利用正方形纸片折叠、观察与发现.
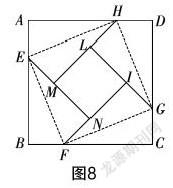
如图8所示,将正方形ABCD的四个角分别向内折叠,取DH=AE=BF=CG,将点A沿EH折叠到点M,点B沿FE折叠到点N,点C沿GF折叠到点I,点D沿HG折叠到点L,发现点M,N,I,L分别在线段EN,FI,GL,HM上.
实践与运用:
(1)请判断四边形EFGH和四边形MNIL的形状;
(2)若DH=AE=BF=CG=b,AH=a,EH=c,你能说说a,b,c有何数量关系吗?(提示:用面积相等的方法去思考)
设计意图 “探究活动3”折叠的图形为“弦图”,是2002年北京第24届国际数学家大会会徽图案. 赵爽在为《周髀算经》写序时提到:“勾股各自乘,并之,为弦实……”图9折叠后的图形就是“赵爽弦图”(如图10所示),利用“4个全等的直角三角形的面积和+中间最小的正方形的面积=折叠后的正方形的面积”得到4× ab+(a-b)2=c2,化简后得到勾股定理;而展开图形也能够通过面积相等构建4× ab+c2=(a+b)2的等量关系,从而得到直角三角形直角边与斜边的关系. 勾股定理是人类早期发现并证明了的重要的数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一. 通过动手操作,让弦图“活”起来,引导学生通过操作弦图,使其很容易发现图中的边、角的关系,通过可视化操作和推理进一步强化学生对弦图的认识和对勾股定理的理解. 同时,通过引入数学史的相关内容,提高学生的数学文化修养.
课后反思
1. 因材施教,活动内容设置应贴近学生的思维特点
一方面要立足初中生的基本“材”质. 根据教育心理学家皮亚杰的认知发展阶段理论,可知初中生的抽象思维水平还不高,处于从直觉经验型思维向逻辑思维过渡的阶段,其逻辑思维层次在很大程度上仍处于形式逻辑阶段,辩证思维还处于萌芽和初始阶段. 因此,初中生对概念的理解、判断、推理在很大程度上离不开直观形象的支撑. 折纸正好实现了几何知识的“看得见”“摸得着”. 另一方面要选好活动课的“材”料. 纸张是生活中最容易获得和接触到的材料,也是可塑性最强的材料之一,充分利用纸张的特性展开活动课程,构建边、角的关系及关于折痕(对称轴)的对称关系,使教学活动的组织实施变得更加容易和更加具有可操作性.
2. 螺旋上升,活动层次遵循“经验—抽象—内化”的渐进过程
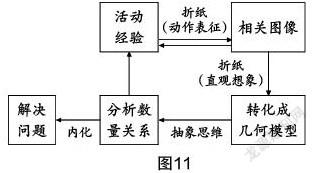
布鲁纳认为,教学过程首先应从直接经验入手(动作表征),然后是经验的映像性表象(表象表征),再过渡到经验的符号性表象(符号表征). 通过折纸活动课程的实施,让学生学会从已有的生活认知(小学时期对折叠纸张活动的基本认知),实现对数、形的理解;从直观到抽象——对数学中边、角数量关系的认知构建,解决一些有关几何图形数量关系的基本问题,使学生在活动中认识并重塑自己的数学知识结构;再进行更高层次上的实验与探索,体会数学的研究方法和构建的知识体系,以及抽象知识的实际应用,提升学生的认知能力,解决实际问题,实现从“直观图形—直观想象—抽象思维”的转变. 通过数学活动更加有助于学生对相关知识点的掌握和深刻理解、对数学本质的深刻认识和深度把握,从而提升学生对数学知识和技能的应用能力. (如图11所示)
3. 驾驭课堂,让思维从“手中”起航“飞翔”
数学活动课程既有动手实操又有数学理论的升华,能否充分驾驭课堂显得十分重要. 一方面,课前准备要充分,根据教学要求设立明确的活动目标,拟定并严格执行课程进度,围绕每一小项活动的教学目标对课程内容进行反复推敲;同时,推演课堂时间控制方案,做到课堂教学松紧有度、收放自如. 另一方面,数学活动课程需要在“做”的过程中“思考”,实现从“听数学”到“做数学”的转变,从用“眼”观察到“手”“眼”并重的转变,从“被动接受”到“主动探究”的转变,学生的直观想象由此会得到进一步拓展,加深对数学知识的理解,提升其分析和解决实际问题的能力.
结束语
列宁指出:“从生动直观到抽象的思维,并从抽象的思维到实践,这就是认识真理、认识客观实在的辩证途径. ”在数学教学中融入活动课程,让学生通过眼、手、脑的感知、思考,培养和拓展他们的直观想象能力.
3840501908292

