问题引领,促课堂有效生成
孔祥菊
[摘 要] 问题是数学的心脏,是思维的引擎,是学习的动力. 好的问题不仅能提高课堂教学效率,还能促使课堂有效生成,发展学生的思维能力. 文章从问题引领数学课堂的实施原则为出发点,以一道习题为例,展示问题引领数学课堂的实施过程,并提出一些思考.
[关键词] 问题;数学课堂;原则
问题是探究的起点,是课堂教学活动实施的主线. 好的问题能激发学生的学习动力,促使学生获得创新意识. 而问题引领下的课堂不仅体现了学生的主体性地位,还能激活学生的思维,使得师生在互动中形成有效的学习共同体. 但是,在当前的数学课堂中,存在着提问方式过于呆板,解决方法较单一,思考问题的学生基本集中在固定群体(学优生)等弊端.
为了充分发挥问题的作用,让问题促使课堂有效生成,笔者在教学实践中经多方面尝试,针对问题引领课堂的原则与实施措施谈一些拙见.
实施原则
1. 自主探究性原則
自新课标颁行以来,学生在教学中的地位一直是备受关注的话题之一. 在强调学生主体性地位的同时,新课标更强调学生获取新知的方式主要以自主观察、体验、探索及自我建构为主. 问题引领的数学课堂,更须注重学生的主体性. 教师可创设和谐、民主的课堂氛围,鼓励学生在问题的引领下主动参与、自主生疑并释疑,在体验中获得深刻的学习感悟.
2. 情境创设性原则
哈尔斯(P.R.Halmos)认为:“问题是数学的心脏. ”课堂中,有疑才有问,有问则有思,而思则促生成. 因此,教师可根据教学内容与学生的实际能力,创设拾级而上的问题情境,鼓励学生积极思考并主动提出问题,活跃思维. 学生在层层递进的问题情境中进行思考、分析、归纳、探索,从而获得积极的情感体验,完成教学目标的同时实现数学思维的发展.
3. 师生共同体原则
新课标引领下的数学课堂,早已摒弃了传统的教师为主体的教学模式. 而今,更强调师生的双边互动,在教师的点拨与引导下,学生积极参与教学活动,并大胆地进行猜想,在自主探究与合作学习中获得更多的新知与技能. 平等的师生关系,让课堂呈现出健康、积极向上的良好状态. 为课堂有效地生成,提供了良好的环境背景.
实施措施
不少学生都有这样的学习体会:一听就懂,一做就错. 究其原因还在于学生没有从根本上掌握知识的内涵,没有能将知识同化并顺应到自己的认知结构中,建构的认知还不足以实现知识的迁移. 为了突破这种障碍,笔者以一道例题为线索,具体谈谈如何让问题引领数学课堂,以实现课堂的有效生成.
例题:某化妆品超市正在销售的一批洗面奶,每天平均销量为20只,每只售价60元,每天该洗面奶的销售额为多少元?
本问题情境非常贴近学生的生活,学生对此产生了比较高的兴致,甚至有个别学生在琢磨洗面奶的品牌. 针对此问,学生积极性很高,争先恐后地举手回答问题. 于初中学生而言,此问异常简单:销售额=单只售价×售出量,即60×20=1200元.
在学生对本题产生了积极的情感时,教师针对本题设计了以下问题链,以促进课堂有效生成,帮助学生实现知识的正迁移.
1. 小试牛刀
问题1:给题设条件添加“每只洗面奶的成本价为20元”的条件,问此款洗面奶的一天销售利润是多少元?
此条件的添加是为了帮助学生区分销售额与利润的区别,难度并不大,大部分学生一看就能明白,几乎不存在解题障碍. 利润=(售价-成本价)×销售量,即(60-20)×20=800元.
2. 精讲试题
问题2:某化妆品超市正在销售的一批洗面奶,每天平均销量为20只,每只售价60元,成本价20元. 为了迎合市场需求,做一些推广活动以增加销售量,超市决定进行降价促销. 经调查,单价每下调1元,超市每天可比原来多出售2只洗面奶. 若想实现每天的利润额为1200元,每只售价应下调多少元?
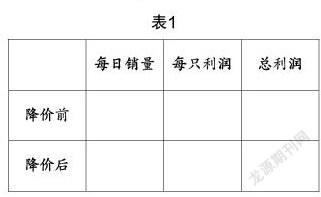
分析:设每只洗面奶降价x元,每天就能多售出2x只,想要利润额达到1200元,则存在这样的等量关系:每日售出数量×每只盈利=1200元. 但此次方程中涉及的数量关系有点繁杂,学生难以一下子理解. 教师可让学生填写表1,让数量关系一目了然,便于解题.
问题3:在问题2的基础上,增加“扣除每天50元水电费的基础上,每天的盈利为1200元”的条件.
分析:增加此条件就是为了混淆视听,看看学生的应变能力. 只要稍加思考就能发现添加此条件后就是将每天的盈利提高到1250元,解题方法与问题2一样. 但是,不少学生在添加此条件后,解题时忽略了这个条件. 对于漏看条件的问题,只要注重加强学生审题能力的训练就可以了. 本题列式为:每日售出数量×每只盈利-水电费=1200元.
问题4:如果把问题2中的“单价每下降1元,可比原来多出售2只”的条件改成“单价每下降0.5元,可比原来多出售2只”,怎么解决此问?
分析:此问看起来没有什么难度,但因数据变成小数,导致不少学生感到有点困难. 其实,只要抓住解决问题2建立的“每日售出数量×每只盈利=1200元”这个关系式,即可找出每日出售洗面奶的数量.
设单价需降低x元能满足条件,每降一个0.5元能多卖两只洗面奶,降个0.5元能多卖×2只. 每天卖出洗面奶的数量就是×2+20只. 将此式代入以上关系式即可.
问题到此,学生对这个利润问题已经掌握得比较透彻了. 此过程,虽然问题由教师提出,但解决问题的过程,都是由学生自主探索而来的. 教师从一道简单习题着手,逐渐深挖此题的纵深,使得问题循序渐进地变复杂,但又有迹可循.
3. 拓展延伸
问题5:假设超市想让这款洗面奶每天都能获得利润最大化,这只洗面奶的售价应该下降多少?
分析:这个问题已经上升到比较高的高度,对大部分学生来说,存在着一定的难度. 解决此问过程还会涉及求二次三项式最值的问题,学生对此只有初步接触,还没有深入理解. 所以问题5的拓展是留给学有余力的学生课后进行探索的,不作为所有学生必须掌握的内容. 此问的提出也凸显了新课标所倡导的“分层教学”原则,让每个层次的学生在教学中都能获得最大化的发展与提升.
本节课在问题链的引领下,有效生成了一个充满智慧的动态课堂. 学生在一个个逐渐深入的问题中自主探索,不仅获得了相应的知识,还体会了遇到此类题万变不离其宗的解题技巧. 不论问题发生怎样的变化,但本题的解题过程都离不开“每日售出数量×每只盈利=1200元”这个等量关系. 这种解题技巧的形成,在凸显课堂有效性的同时,也让学生感知到数学思想的重要性.
教学思考
实践证明,问题引领课堂的教学方式对课堂生成具有显著的作用,它能有效地激发学生的学习热情,促使课堂流畅、顺利、丰富并有效生成. 但是,部分教师在运用这种教学方式时,在问题链的设计上存在一些问题,具体表现在:
(1)认为过于简单的问题没有价值. 其实,简单的问题作为学生思维的起点,具有埋伏笔、作铺垫等作用. 尤其对于认知水平较低的学生来说,简单问题显得尤为必要. 这也是新课标所倡导的“面向全体学生”的教育理念.
(2)问题梯度掌握不准确. 问题的台阶过小,学生不需要任何思考就能直接获得答案,这样的问题缺乏实际价值;而台阶过大的问题,学生即使“跳一跳”也够不着,这种问题就丧失了存在的意义.
因此,问题链的设计需要教师精心准备,一般可从以下几方面着手:明确问题链的主线(核心),所有的问题须围绕主线而展开,不能漫无目的地想到哪儿,问到哪儿;控制好问题的难易度,根据实际情况制定问题;问题与问题之间的梯度合理,只有落在学生最近发展区内的问题才能促使课堂的有效生成.
总之,问题引领的课堂生成需采用“低起点、小步子”的方法,逐层深入、循序渐进地兼顾每个水平层次的学生. 让学生通过自主探索,以深化对知识的认识,形成能促进学生可持续性发展的数学综合能力.
3109501908203

