指向提升学力的“问题链”教学策略
孟凡亮

[摘 要] “问题链”可以触动教学目标,可以激活教学过程,基于“問题链”的教学设计是生动的,也是具有魅力的. 文章首先对“问题链”进行解读,进而展示了“垂直平分线性质的逆定理”一课的教学设计. 该教学设计以问题链的形式呈现,提出对准教学目标设计问题和以问题驱动为设计理念的教学策略.
[关键词] 问题链;学习能力;策略
问题是思维的动力,更是数学的灵魂,离开了问题的数学课堂是失去灵气的,没有问题的数学课堂无法激活学生思维. 可见,问题是提升数学课堂效率和发展学生思维能力的关键所在. 初中数学对学生抽象思维的要求较高,很多时候有待解决的问题具有较大的难度或具有较强的灵活性,此时需要教师设计一连串的问题来启智导学,这样的一连串的问题就是“问题链”. “问题链”作为一种常见的问题设计方式,在初中数学教学中意义重大,可以激发学趣,可以引导学生进行积极的思维活动,可以有效化解教学重难点,可以训练并发展思维,可以促进学生自主构建,可以提高学生的数学学习能力.
“问题链”的解读
那么,什么是“问题链”?笔者认为,“问题链”是问题结构的表现形式之一,通常就是基于数学本质,对原问题进行特殊化处理,将其分为层层深入的多个小问题,这多个小问题之间具有隐性的内在联系却又相对独立,通常前一个问题是后一个问题的铺垫,后一个问题是前一个的递进,就这样,将新知学习转化为解决一系列问题,让学生在一步步的问题解决中,自然地进行新知的摄取和能力的攀登,以实现自主建构,完善数学的知识体系.
“问题链”教学策略案例
既然“问题链”教学可以引导学生主动思考、自主探究和自主建构,那么该如何将其落实于具体的教学实践中去?本文,笔者在深钻教材和深入了解学情的基础之上,以“垂直平分线性质的逆定理”的课堂教学为例,谈谈教学中如何以“问题链”为导向去揭示数学概念的形成过程和数学知识的内在关联,让学生经历“思考—探究—发现—反思”的思维过程,提高学习能力.
1. 温故知新——指向学生经验,引发思考
问题1:一起回忆一下,上节课我们学习了什么?请试着用几何语言进行表达.
问题2:谁能说出垂直平分线性质的逆命题?这是一个真命题吗?
设计意图 温故而知新,这里将“问题链”作为教学的起点,教师的问题设计具有一定的指向性. 教师探寻到学生学习心理与问题的联系,问题1以回忆旧知来引入新课,可以充分调动学生的知识储备,让学生去动手操作和积极思考,为问题2的解决奠基. 问题2的提出则是为了指导学生展开合情猜想,并适时引出课题,培养学生的逆向思维.
2. 数学探究——指向探究过程,获得建构
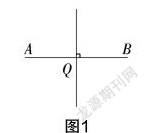
问题3:请找出图1中到线段AB两端距离相等的点.
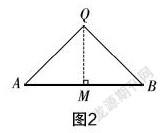
问题4:请利用圆规在图2中找出一点Q,使得QA=QB,并说一说你作图的方法.
问题5:利用圆规在图2中再找出一点E,使得EA=EB. 请画出直线QE,并说一说线段AB和直线QE有何关系.
问题6:诸如点E的点有几个?这些点都在哪个位置?
问题7:如图1,试证明到线段AB两端距离相等的点都在其垂直平分线上.
问题8:试着画出线段AB的垂直平分线.
设计意图 问题链的呈现将完整地再现知识的发生和发展历程,让数学知识的价值得以最大化,使得数学课堂变得生动而流畅. 本环节中,教师首先让学生自我尝试着去解决问题,学生经过思考易想到利用刻度尺进行探究的策略;接着,让学生进行动手操作,在反复尝试的过程中获得更一般的方法,以渗透从特殊到一般的数学思想;然后,鼓励学生进行猜想,并获得发现“这样的点有无数个,且位于线段AB的垂直平分线上”,这样的感觉仅仅是学生的猜想,显然需要进一步进行验证;之后,引领学生讨论和归纳得出逆定理,并作图以符号语言表示;整个探究过程中,问题7是教学的重难点,要知道任何定理的得出都需要经历严密的推理,那么下一步自然是进行推理验证,此处应引导学生分成两种情况讨论,即在线段AB上和在线段AB外,借机渗透分类讨论的数学思想,并培养演绎推理能力;最后,通过作图,让学生回忆作图经历,总结作图步骤,深化认识.
3. 应用提升——指向应用与拓展的深加工
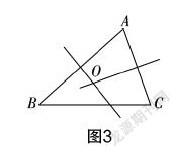
问题9:已知△ABC,在图3中分别作出边AB与AC的垂直平分线l和l,且l与l交于点O,那么点O是否在边BC的垂直平分线上?请予以作图观察.
问题10:请试着证明点O也在边BC的垂直平分线上.
问题11:请试着用尽可能多的方法解决以下问题:如图4,已知AB=AD,BC=DC,且点E在AC上,证明:EB=ED.
设计意图 以问题9为载体,为学生打造巩固作垂直平分线方法的要素,同时鼓励学生直观猜想结论,为进一步证明奠基;问题10则再一次从合情推理向着演绎推理迈进,让学生在证明中获取认识. 最后抛出一道应用问题,不少学生拿到题目立刻想到用全等知识进行证明,此处笔者提出用多种方法解决的要求,就是为学生尝试利用新知来解题提供动力,让学生体会创新解法的简洁性和灵活性,同时有助于学生实现自我突破,发展逻辑推理素养.
4. 课堂小结——指向学力提升和思想感悟
问题12:通过今天学习,你收获了什么?
设计意图 以问题为驱动,让学生在回忆中感悟知识间螺旋上升的关系,感悟数形结合、分类讨论及符号化数学思想是数学教学的精髓,在基于“问题链”教学的过程中不断浸润,发展空间观念和演绎推理能力,最终提高学生的学习能力. 此处,学生由于认知水平、学习经验和学习能力等方面的差异对本节课会有不同的感悟.
基于课例的几点思考
问题作为课堂教学的一个重要支点,承载着激趣引思、启迪思维和质疑问难等重要作用,从现代理论所倡导的“问题链”教学模式不难看出,问题设计是教学的必要环节,是课堂教学的驱动所在,在数学教学中设计“问题链”,笔者认为有如下策略:
1. 对准教学目标设计问题
教学目标是教学过程所需达成的结果,也是展开课堂教学的总纲. 传统教学中,我们所设计的教学目标往往笼统而宽泛,这样的教学缺乏目的性,从而使得教学缺乏实效性. 从而,教师应在课堂做好充足准备,所设计的问题要对准教学目标,这样才能彻底摒弃传统教学的目标过于宽泛的情形. 本节课中,教师基于教材与学情准确定位教学目标和重难点,立意时做了双重考虑,一方面,通过解决问题链中的系列问题来突破本课的重难点“证明到一线段两端距离相等的点在该线段的垂直平分线上”,这是对逆定理深化理解的一个必要步骤,是学生继续建构的过程. 另一方面,通过问题链的指引,不仅完成了重难点的突破,更是有效渗透了多个数学思想方法.
2. 以问题驱动为设计理念
问题链的序列性有效克服了传统教学中提问的细碎、零散和随意,让学生在解决问题链的过程中习得知识、获得解决问题的策略及提高学习能力. 本课中,教师仅仅是提供了问题链,并在学生问题解决中及时、适时做出评价,问题解决的主动权在于学生,归纳提炼的工作也是在师生交流中完成的,并在主动参与和积极讨论中将每个学生的观点纳入课堂. 由于在解决问题中获得的方法,深化了学生的理解,更重要的是转化成了学习能力,以便在之后的学习中有效提取.
总之,指向提升学力的问题串设计并非易事,在实施“问题链”教学的过程中,教师需要深入钻研教材和学生,所设计的问题要对准教学目标,突出教学重难点,需问于学生有疑问的地方,促进其对问题的理解. 更重要的是以问题驱动为设计理念,引领学生积极思考,在主动参与和积极讨论中将每个学生的观点纳入课堂,只有这样,才能让数学课堂更具活力,从而有效提高学生的学习能力.
3033501908208

