“再创造”范式下的一题一课复习
胡柳青

[摘 要] 学习数学的唯一正确方法是实行“再创造”,也就是学生要学习的东西由自己去发现或创造出来. 教师的任务是引导和帮助学生进行这种“再创造”的工作,而不是把现成的知识灌输给学生. 文章以“反比例函数k的几何意义”为例,结合一题一课复习详尽地展现了这一范式操作的可行性和科学性,阐述实际操作中如何谋篇布局,提质促效.
[关键词] 再创造;一题一课;数学复习
问题提出
弗赖登塔尔反复强调:学习数学的唯一正确方法是实行“再创造”,也就是学生要学习的东西由自己去发现或创造出来. 教师的任务是引导和帮助进行“再创造”的工作,而不是把现成的知识灌输给学生. 因此,进行有指导的“再创造”无可非议是每个数学教育工作者必须领会和遵循的教學思想.
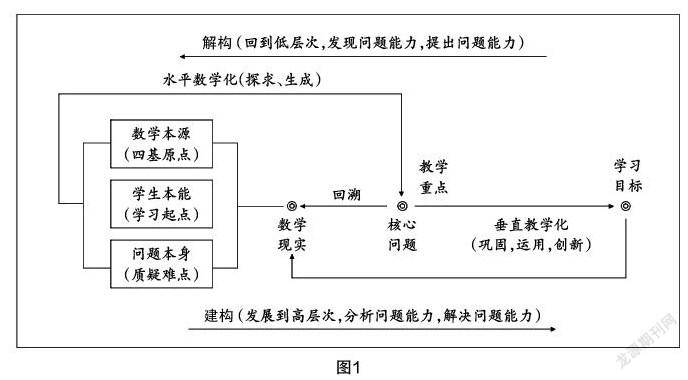
省特级教师、正高级教师盛志军于2017年成立桐庐县、富阳区杭州市农村名师工作室. 工作室以弗赖登塔尔的“再创造”理论为指导,开展《再创造:基于核心素养的初中数学课堂范式研究》的课题研究(浙江省教研规划课题G2019028). “再创造”教学范式显著特征就是强调学生再创造者的地位,经历知识的再创造过程,注重与生活的联系和应用. 根据弗氏相关理论,我们把“再创造”教学的基本理念描述如下(如图1):
(1)确定处于学术状态的“现成数学”中的核心内容作为教学材料;
(2)把核心问题回溯到学生的现成数学状态中去,进而发现问题、提出问题、理解问题;
(3)引领学生数学认知联结(寻求兴趣点、生长点和疑难点等),通过“水平数学化”分析问题,初步解决核心问题;
(4)巩固核心内容,并以此为起点,“垂直数学化”,拓展探索,发现新的问题,水平探索……螺旋上升,循环往复.
三年来,工作室开展了丰富多彩的实践活动,就如何实施“再创造”教学进行有益探索并构建基本范式(如图2). 《反比例函数k的几何意义》为工作室成员卢老师的一堂示范课,现摘录如下,以飨同仁.
课例展示
1. 复习课题
反比例函数k的几何意义.
2. 复习目标
(1)经历从函数图像上任意一点向x、y轴作垂线所得三角形(矩形)面积的探索过程,进一步理解函数系数k的几何意义.
(2)通过探究函数系数k的几何意义,感受数形结合和转化等数学思想、数学方法.
(3)能够灵活运用函数系数k的几何意义,解决一些比较综合的问题,理解函数系数k的本质.
3. 学情分析
浙教版教材中,学生在八上学习函数、一次函数,在八下学习反比例函数,在九上学习二次函数,在九下学习三角函数等. 反比例函数学习,可以促进学生进一步理解函数概念,熟悉研究过程与思考方法,为后续学习奠定基础. 在学习中,学生对于函数解析式等理解相对透彻,对几何意义的理解尚显不足. 反比例函数的问题解决,通常会与图形面积交汇一起,通过对应关系渗透数形结合思想,从而理解函数系数k、函数解析式和函数图形的内在联系,建立“数”“式”“形”的一一对应关系. 为此,本节课将在原有模型基础上构建新模型,通过水平数学化和垂直数学化,激发学生更深层次的思维活动,实现反比例函数k的几何意义的“再创造”学习. 本节课确定如下几点.
中心:反比例函数k的几何意义;
重心:反比例函数k的几何意义的综合问题探究;
核心:反比例函数中数形结合思想的运用.
4.思考方向
函数背景考点多. 反比例函数知识繁杂,需要熟练掌握概念、图像、性质与应用等. 知识间不是独立存在的,往往相互联系,综合程度比较高. 反比例函数已然成为中考的常考内容,形式越来越新颖,探索性越来越强. 本节课以反比例函数系数k为突破口,探究其与矩形、三角形面积的内在联系,将知识进行整理、融合、提升,对学生分析和解决问题的能力提出更高要求.
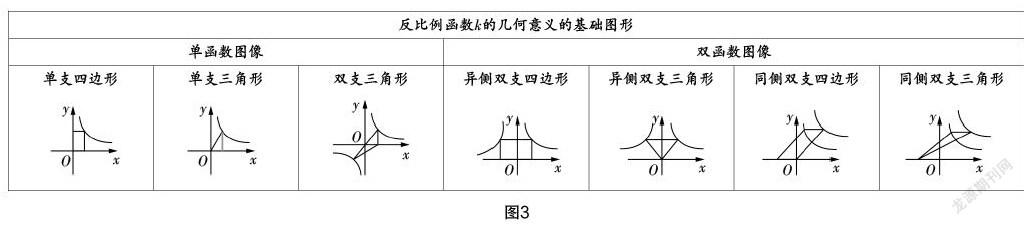
图像变化种类多. 利用k的几何意义解决反比例函数与面积的综合问题,通常会在基础图形(见图3)上变化延伸,从而产生更多图形. 如何在众多变形中找出内在联系,进而有效解决,就需要他们熟练掌握基础图形,概括归纳寻求共性,进而找出通解通法.
思维提升阻碍多. 反比例函数是最基本的初等函数,是学习二次函数、三角函数乃至对数与指数函数的基础,系数k与生俱来的代数意义和几何意义,完美体现了“数形结合”. 已知系数k,就应该联想到相关图形面积,考虑系数k的几何意义;反之,如果知道相关面积信息,就应该考虑系数k的代数意义. 学习时,学生们往往会割裂其联系,顾此失彼. 这就需要教师引导学生打破原有的知识壁垒,从复杂图形中抽丝剥茧地找出基础模型,寻找解决问题的钥匙,实现“再创造”的学习.
基于以上分析,本节课将通过模型来研究题型,依托一题多解和多题一解,对反比例函数系数k的几何意义进行再次理解和归纳,从而实现知识、技能和思想方法上的“再创造”.
5. 设计思路
环节一 本源回溯
(1)我们已经学过一次函数、反比例函数和二次函数等知识,请思考:
问题1:平面直角坐标系上有一点A(1,6),你能得到过点A的函数吗?如果有点A(1,6)和点B(2,3),你能得到过点A,B的函数吗?如果有点A(1,6)、点B(2,3)、点C(-1,-6),你能得到过点A,B,C的函数吗?
问题2:①如图4,如果有点A(1,6)、点B(2,3)、点C(-1,-6)和点D(-2,-3),你能得到过点A,B,C,D的函数吗?你能找出图像上的其他点吗?
②如图5,在函数图像上,过点B向x,y轴作垂线,垂足为E,F,则OEBF面积为多少?若P(x,y)是图像上任意一点,过点P向x,y轴作垂线,垂足为M,N,则OMPN面积为多少?
③如图6,过点A,B,C,D作x轴(或y轴)垂线,该点、垂足与点O构成四个三角形,求三角形面积. 如果P是函数图像上任意点,作x轴(或y轴)垂线,求垂足、点P、点O所构三角形面积.
设计说明:本源回溯是整个课堂教学的基础,务须符合认知需求,强调知识衔接. 教师从经过一个、两个、三个、四个点的解析式入手,从本源上引导学生回溯系数k与几何面积的联系,关注k的代数意义与几何意义. 只有本源回溯精准,才能从学生实际出发,开展适合学生认知的学习,以此来加强教学活动设计的实效性,为“再创造”提供可行条件.
环节二 新知再造
设计说明:新知再造要引导学生梳理知识网络,在整体结构中理解数学本质. 学生认知结构、活動经验等均有不同,有独特“数学现实”. 教师课堂教学“再创造”,要根植学生的“数学现实”和“思维水平”,创设丰富的学习活动,分别经历知识的水平数学化和垂直数学化,完成“再创造”,达成知识建构. 拓展一,先求出点A,B,延长BO交另一支于点C,如图14,利用对称性得BO=CO,△AOB与△AOC面积相等,求得△AOB面积. 拓展二,由一支曲线上两点转化为两支曲线的特殊点,如图16,连接OA,OB,得S△APB=S△AOB,利用模型求得S△APB=S△AOB=S△AOC-S△BOC=2. 拓展三,将特殊点又转化为一般点(如图18),将同一象限的两点转化为不同象限的两点(如图20、22),仍可用类似方法求解:问题1,如图19,过A,B作x轴垂线AM,BN,转化为四边形与三角形面积的和(差):S△AOB=S△AOM+S四边形AMNB-S△OBN,与例题不同的地方是:由于点在不同函数上,故两个三角形面积不相等;问题2则与拓展一完全相同,可利用中心对称性,如图21,延长BO交双曲线另一支于点C,得S△ABO=S△ACO;问题3则与前两问题的解法相似,如图23,转化为四边形与三角形面积的和(差). 教师逐步引导下,找出问题共性,一题多解,多题一解,体会利用基础模型解决复杂问题的便利,最终实现数学知识和思想方法的“再创造”.
设计说明:后续联结是整节课的知识回顾,也可以是下节课的本源回溯,但不能和预习与复习混淆. 后续联结是巩固所学知识、形成技能方法、培养良好思维、发展核心素养的重要途径. 问题选择时也要适当提升难度,培养发散思维,提升创新思维,在持续发展中不断“再创造”. 上述题目均选自2020年中考真题,着重考查学生是否掌握了反比例系数k的几何意义,起到课后检测的作用.
反思跟进
“再创造”范式下的一题一课复习,是一个让学生在更高视野下的构建知识的过程,也是一个让学生在更深思维下的感受生长的过程,还是一个让学生在更精文化下的发展自我的过程. 本节课从一个主问题开始,以点带面、由浅入深地复习整章知识,通过反比例函数k的几何意义串联形成一条主线,不同的知识又由这条主线关联在一起,从而使得复习教学走向简约而高效.
1. “再创造”范例下的一题一课,要选准一个好题
数学复习应该有一定的广度和深度. 广度是横向上的容量与范围,深度则是纵向上的数学思考. 一题一课,知识的掌握、方法的提升、思想的领悟都凝聚于题,一题的选择就尤其关键. 首先,知识内容应该是主干知识、重要思想,而不能旁枝逸出,轻重不分;其次,知识含量应该充足,或者可供拓展,能进行丰富和必要的发散提升;最后,知识种类应该丰富,是多种类、多样化的,既要有知识、技能,又要有思想、方法和活动体验. 教学时还要对所选例题进行充分的、必要的、精细的打磨,要将所选问题与教学目标进行关联,弱化无关知识,强化核心思想,从而保证最终解决的问题具有很高的价值.
2. “再创造”范例下的一题一课,要突出一个主体
《义务教育数学课程标准》指出“有效的教学活动是学生学与教师教的统一,学生是学习的主体,教师是学习的组织者、引导者与合作者”. “再创造”范例下的一题一课就是要强调“学生之本位”,还“课堂之本色”. 教学中,要始终以学生为主体,尝试引导学生参与变式、拟题活动,提出一些富有探究价值的问题,在问题中提升,使得学生对知识理解更为全面、更加透彻,让不同层次学生有不同程度的理解深度,让个性相异学生表达自主独特的思考路径,还要让学生的疑惑引发教师的思考,将被动灌输转变为主动探究,从而将复习教学转化为生动有趣、学知育人的有效课堂.
3. “再创造”范例下的一题一课,要经历一次生长
教育的出发点和落脚点就是让学生经历成长、见证成长、完成成长. “再创造”范例下的一题一课复习秉承的是一种让学生在复习课中成长的理念,讲究的是一种让学生在复习课中成长的策略. 具体地讲,“再创造”范例下的一题一课,正是通过创设问题情境、独立自主探究、生生合作交流、师生成果展示等过程,让学生充分经历观察、类比、猜想、思考、验证、推理、转化等过程,让他们感受到数学可以如此有趣、轻松地学,而且能够理解与掌握研究数学、解决问题的常用思路和一般方法. 唯有如此,才能让核心知识、重要思想的真正价值落到实处,也只有这样,才能确保教学方向的准确无误,学习成效的显著提升,才能真正激发学生的数学学习兴趣,启迪数学智慧,开拓思维能力,培养创新意识,提高数学素养.
以往,在浩瀚的图书馆中寻找多日的资料,今天,借助百度、知乎可以信手拈来;以往,“知识就是力量”,未来,“思维才是力量”;以往,在职场中稳操胜券的是“有知识的人”,未来,在职场中独领风骚的将是“会学习的人”……“再创造”就是让学生参与发现、探索、创造知识的全过程. 只有教师“再创造”地教才能为学生“再创造”地学提供肥沃土壤,才能使学生的“再创造”能力不断地得到发展.

