以学定教,顺学而导
肖慧 虞秀云
[摘 要] 基于学生学习路径分析的基本框架,从理解学习目标、确定学习起点、分析学习路径、设计并实施教学任务这四个步骤对“圆的面积”一课进行教学设计,从学生多元的学习路径出发设计适切多样的教学路径,旨在培养学生数学思维的个性化,使不同学习路径的学生得到最优发展。
[关键词] 学习路径分析;圆的面积;以学定教
学习路径,是指学习者为达到学习目标所进行的一系列学习活动的过程。学生已有的知识经验、学生的思维过程以及学生对知识的表征方式是构成对学生学习路径分析的三个主要方面 [1]。基于学生学习路径分析的数学教学则包括以下四个步骤:理解学习目标、确定学习起点、分析学习路径、设计并实施教学任务 [2]。本文将结合这四个步骤,基于学习路径分析设计圆的面积教学,就如何充分理解学生,实施有效教学做进一步探究。
“圆的面积”是人教版小学数学六年级上册的内容,是学生所接触的第一种曲线图形的面积计算。它作为小学“图形与几何”内容的重要组成部分,是平面图形测量中由直线图形向曲线图形过渡的关键点。《义务教育数学课程标准(2011年版)》对该内容的要求是“探索并掌握圆的面积公式,并能解决简单的实际问题”。根据课标的要求,学生既要经历圆面积计算公式的推导过程,掌握圆的面积计算公式,又要能够灵活运用其解决实际问题。
一、理解学习目标
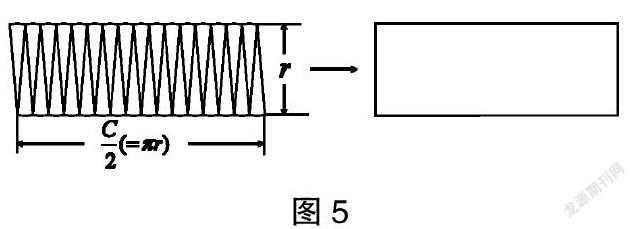
北师大版、人教版、浙教版以及苏教版教材中关于“圆的面积”计算都采用了“分割—拼合”法,即将圆等分成若干个小扇形,再将其拼合成近似的长方形,进而根据长方形的面积计算公式推导出圆的面积计算公式。由于前面学习过平行四边形、三角形、梯形等平面图形的面积,积累了大量利用数方格和“分割—拼合”法研究直线图形面积的经验,学生较容易想到运用这两种方法求解。但方格法操作麻烦,误差较大,利用“分割—拼合”法转化成学习过的平面图形则是较为精确求解圆面积的主要方法。公式推导的过程中涉及转化和极限的数学思想,考虑到学生已有的知识经验和思维特点,对极限思想的理解将是本节课的一大学习难点。
因此,为了帮助学生突破难点,真正理解“圆的面积”这一内容,现将学习目标分解为以下几点:
1. 正确理解圆的面积的概念;
2. 把圆分割、拼合成学过的平面图形,体会转化后的图形与圆之间的关系,积累研究图形面积的经验;
3. 经历操作、观察、分析、想象等活动,推理归纳出圆的面积计算公式,体会化归和极限思想,感受图形间的联系和转化;
4. 理解圆的面积计算公式,能正确计算圆的面积,解决实际问题。
二、确定学习起点
准确了解学生的学习起点是进行教学设计的前提和依据 [2]。确定学生真实的学习起点可以通过学生访谈、进行相应的课前测试、依据教学经验或者已有研究等途径来实现。关于“圆的面积”这一内容,通过对已有文献进行研究,发现大多数学生研究圆的面积主要采用数方格、与外切或内接正方形进行比较、分割成原来学过的图形或者均分为小扇形等方法,以及部分学生没有深刻理解面积的定义,容易将圆的周长与面积的概念混淆;少数学生在第一次接触曲线图形的面积计算时没有任何思路,存在学习困难;知道圆的面积计算公式的学生中大部分不清楚公式的推导过程,不理解公式的实质意义等。
对这些问题进行分析,了解学生存在的学习困难,找准学生在学习圆的面积时的认知起点,确定真实的学习起点,进而帮助学生逐步完成知识的建构。
三、分析学习路径
为了实现圆面积推导方法的多样化,将提供方格图以及不同等分的圆形学具,让学生在动手操作中积累基本活动经验,体会转化和极限的数学思想。根据对学习目标的理解以及学习起点的分析,确定了以下的学习路径:(1)动手操作,自主探索圆的面积;(2)结合同伴的求解方法,通过对比判断寻求研究思路;(3)借助直觀演示,分析想象,体会转化和极限的数学思想,推导圆面积的计算公式;(4)沟通不同角度的面积推导公式之间的联系,理解圆的面积公式的本质。
四、教学过程设计
1. 问题情境引领学生探究新知
活动1:给出问题情境,提出研究问题。
问题情境:(课件呈现)李大叔打算新建一个半径为15m的圆形牛栏,想要沿牛栏边沿打上木桩,里面种植牧草。如果每隔2m打一根木桩,大约要打多少根木桩?每平方牧草10元,植草需要花费多少钱?
提示学生思考:要求木桩的数量,需要先知道什么?计算公式是什么?要求植草花费的金额,需要先求什么?
【设计意图】 创设真实问题情境,帮助学生复习旧知,厘清圆周长和面积的概念,激发学生的求知欲,并提出接下来所要研究的问题。
2. 经验激活阶段思考研究方法
活动2:引导学生思考研究圆的面积的方法。
问题1:前面我们学习过哪些平面图形的面积,推导面积计算公式的过程中用到了哪些方法?
问题2:你打算用什么方法来研究圆的面积?
【设计意图】 沟通新旧知识之间的联系,激活学生已有的关于直线图形面积计算的知识经验,促成迁移,进而帮助学生在自己经验范围内找到研究曲线图形面积的可能方法。
3. 问题串引领思维纵深发展
活动3:通过问题串的引导,增进新知。
学生动手实践,自主探究(教师巡视指导,先挑选几份选用方格法的学生作品)。
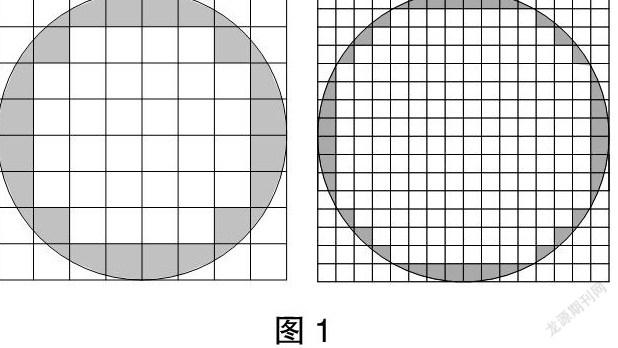
教师展示学生作品(如图1),并让学生汇报自己的思路。
问题3:他们是用什么方法来求解的?
问题4:你认为以上哪个会更接近圆的面积?为什么?
问题5:如果想要更准确地计算圆的面积,该怎么办?
我们发现利用数方格的方法,可以把一个个面积单位累加起来计算圆的面积,方格分得越小,估计值就会越接近圆的面积。
【设计意图】先从学生最容易想到的数方格法入手,通过对比判断哪种做法会更接近圆的面积来渗透极限思想,让学生在动手操作和思考分析中体会该方法的局限性,为之后探索更科学、合理的计算方法打下基础。
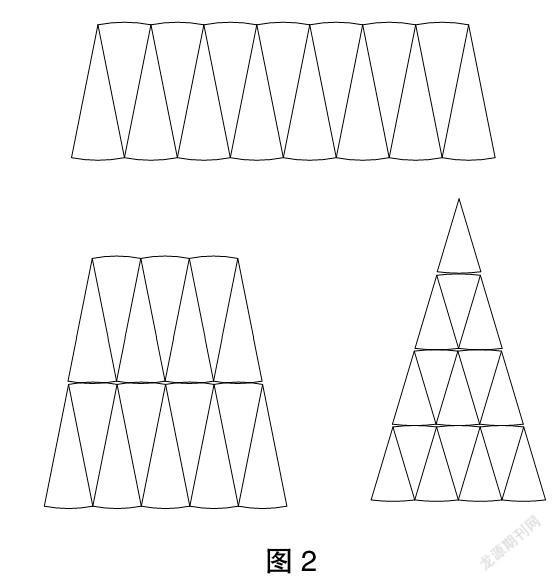
教师继续展示学生作品(如图2),让学生汇报自己的思路。
问题6:这些方法之间有什么共同之处?这一做法好在哪?
针对第一种拼法,教师选取将圆8等分以及16等分拼成的图形进行展示,引导学生观察。
问题7:观察这两位同学的作品,你们有什么发现?
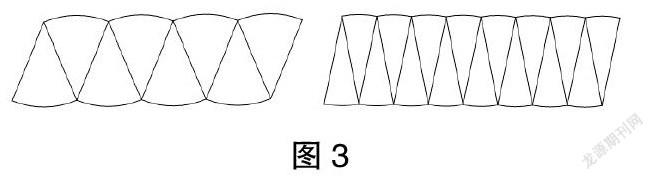
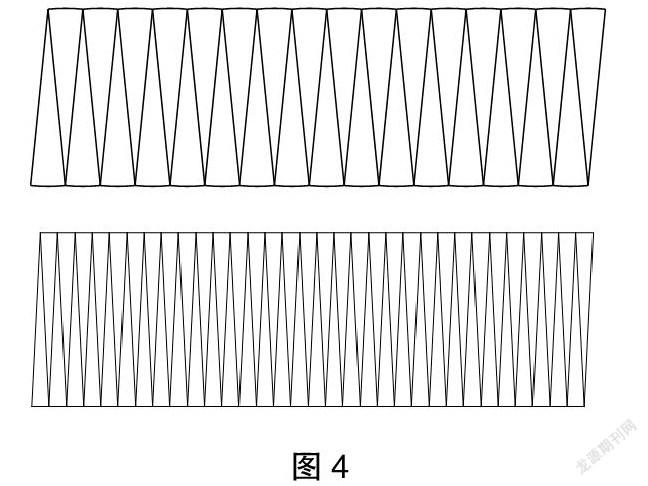
教师利用课件演示将圆平均分成32等份以及64等份后再拼起来。
问题8:再继续等分下去,分成128份后拼成的图形会有什么变化?分成256份呢?如果一直无限分下去,等分成无数份,会拼出怎样的图形?
问题9:针对第二、三种拼法,如果也一直无限分下去,等分成无数份,又会拼出怎样的图形?
【设计意图】 通过学生汇报交流、教师问题引领的方式,促进学生思考,鼓励学生用自己的方式解决问题,理解并欣赏他人的解法。始终以转化和极限思想的渗透为主线,从多元的学习路径设计符合学生认知规律的教学,尊重学生思维的个性化和多样化。
4. 水到渠成推出面积公式
活动4:继续追问,突破难点,推导公式。
问题10:拼成的平行四边形(长方形)与原来的圆之间有什么联系?
引导学生找到拼成后的近似长方形的长和宽与圆之间的关系。
问题11:你能推导出圆的面积计算公式吗?
问题12:前面还把圆转化成三角形和梯形,你能试着利用不同的转化图形来推导圆的面积计算公式吗?
【设计意图】利用多种转化图形来推导圆面积的计算公式,从不同角度的探索中体会转化思想。
问题13:回到活动1,你能计算出种植牧草所需花费的金额吗?
5. 探寻历史追本溯源
教师利用课件展示数学家们求解圆的面积的历程。
【设计意图】 引入数学史,介绍相关的历史背景,能够激发学生的学习兴趣和求知欲,使学生了解知识的发生、发展过程,从而促进学生更系统全面地理解数学。
6. 总结回顾,体会感悟
(1)梳理圆面积计算公式的推导过程;
(2)總结本节课所涉及的数学思想方法;
(3)掌握研究曲线图形面积的方法。
五、结语
一堂课就如同一场旅行,事先我们会做好所有的计划,但在旅行的过程中往往会因为各种情况而做出调整,或者改变行程,或者改变目的地的顺序。课堂教学亦是如此,所有课前的教学安排与假想的教学路径都不应该是直接照搬。学生学习的过程是思维碰撞、生发智慧的过程,在这个过程中,他们所选择的解决问题的方法都是不尽相同的。为了实现教学效果最大化,教师应该尽可能多地照顾到所有学生的思维方法。在设计并调整教学时就需要教师理解学生,了解学生原有的知识经验进而分解学习目标,找准教学的起点和重难点,确定思维的障碍点,获取并分析学生的学习路径,从多元的学习路径设计适切的教学路径,以学定教,在培养学生个性化发展的同时优化学习路径,使不同学习路径的学生得到最优发展。
参考文献:
[1] 张春莉,刘怡. 基于学生学习路径分析的教学路径研究[J]. 中小学教师培训,2015(09).
[2] 章勤琼. 基于学习路径分析的小学数学教学:概述与基本框架[J].小学教学,2019(14).

