渗透“对应思想”，为课堂增效导航

潘玲燕

[摘  要] 数学思想是数学文化的精髓，是学生建立和体会数学与外部联系的基本途径，对他们的后续发展有着重要的影响。而对应是基本的数学思想之一，在课堂中适时地融入对应思想，可以帮助学生建立解决问题的策略意识，实现知识有形化，思维可视化，学习简易化，不断提升他们的数学综合素养，构建厚实的数学课堂。

[关键词] 对应思想;小学数学;学生

苏步青教授曾说：“看书要看到底，书要看透，要看到书背面的东西。”而数学书背面的东西，指的就是蕴藏于知识背后的数学思想，它是数学思维的基本方法，也是培养学生数学核心素养的重要组成部分。新课标强调在数学课堂教学中，不仅要关注基础知识、基本技能，还要关注学生在学习活动中有没有领悟到数学思想。而对应思想就是数学思想的一个重要分支，将其渗透于学生学习数学的过程，有助于降低学习的难度，探寻有效的解题策略，学会数学思考和表达，不断提升数学综合素养，使其真正走出“山重水复疑无路”的迷茫，畅享“柳暗花明又一村”的欢畅。

一、运用对应思想，培养良好数感

数感是人们对数及数运算的感觉，是一种心智技能。可见，培养学生的数感，是小学数学课堂教学的重要任务，但很多老师认为，小学生年龄小、理解能力差，数感难以形成，要想寻找到有效的培养方法，并非是一件易事，其实这种看法是片面的。实际上，在小学数学课堂教学中，教师可以从学生的生活入手，将生活中事物的数量与数字建立对应关系，然后抽象出数，帮助他们理解数的意义，这样既可以在无形之中拉近学生与所学知识的距离，又可以促进学生数感的形成。

在教学“5的认识”时，教师让学生们伸出一只小手，竖起4个小指头，教师微笑着问：如果再竖起一个指头，是几呢？引出“5”，接着让学生拿出计数器，边拨珠，边数。让学生意识到物体不同，但数目相同，都是5个。教师在屏幕上将这些具体的事物隐去，剩下5个点，剩下点子图，并顺势抛出问题：你能在点子图旁边画出自己喜爱的图形吗？在这个环节中，教师将指头、拨珠与点子图一一对应起来，让学生认识数字5。教师让学生拿出5根小棒，将它分成两堆，看看可以怎样分？通过物与物、数与物之间的对应关系，从而强化学生对5的认识，很好地培养了他们的数感。

上述案例，教师巧用对应思想，让学生从具体的实物中抽象出点子图，顺利地抽象出数字5，经历了从模糊到清晰、由具体到抽象的学习过程。在这样的学习活动中，不仅可以让学生的数感意识得以萌芽，还可以使他们获得丰富的表象和富有生命力的数学知识。

二、挖掘对应思想，升华学生认知

“空间与图形”是数学四大领域之一，通过这部分内容的教学，旨在培养学生的想象力和空间观念，发展学生的核心素养。在学习这部分内容的过程中，如果学生不能在纷繁复杂的变化中，正确地把握住事物之间的对应关系，就无法找到解题的途径。尤其在平行四边形和三角形面积计算的教学中，更要注重渗透底、高对应的数学思想，让学生找到解决问题的思路，提升他们的辨析能力。

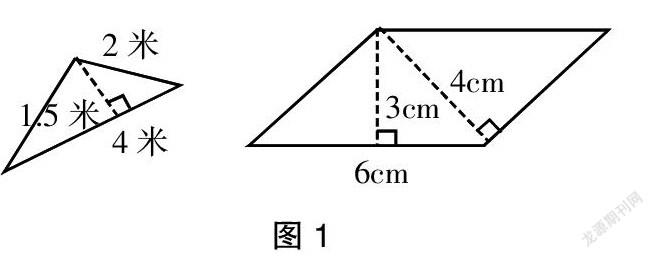
如教学平行四边形和三角形的面积计算公式后，教师发现如果图形中，只给两个数据，学生解答时，正确率就很高，当题目中植入多余条件时，会有很多同学出错，这是什么原因呢？因为学生们在解答题目的过程中，并没有遵循底高对应的思想，而是机械地套用面积计算公式，并没有真正理解所学知识。如计算图1中的三角形面积时，因为高1.5米对应的底边长度是4米，计算这个三角形面积正确的方法是：1.5×4÷2，而有的学生会用1.5×2÷2。图2是一个平行四边形，大家都知道，平行四邊形有两种不同的“高”，计算面积时，有两种不同的方法，但计算出来的结果应该是一致的。要计算出这个图形的面积，只能列出算式：3×6，列式的依据是底、高对应才行。

上述案例，教师针对学生在学习过程中的易错点，通过具体的习题，让学生意识到底高对应的重要性，避免他们在后续的学习中出现同样的错误，使他们获得条理化、系统化、整体化的知识，也强化了数学思考方法，提升了课堂教学效益。

三、融入对应思想，降低学习难度

“数”和“形”是数学研究最基本的两个对象，也是数学发展进程中的两大支柱。“数缺形时少直觉，形少数时难入微。”可见，数与形是相互联系的，两者不可分割，否则会让数学失去应用的活力和精彩。在课堂教学的过程中，教师既要让“数”与“形”各展其长，又要让这两者做到优势互补，相辅相成，达到逻辑与形象思维的完美统一。而渗透对应思想，就是有效的途径之一，可以充分调动学生的感官融入学习，降低学习的难度，构建新的认知体系。

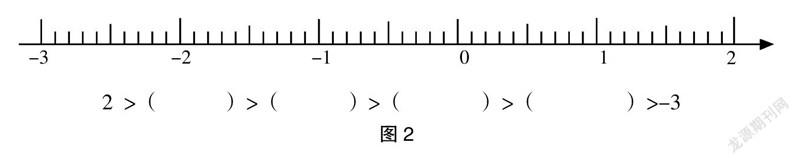
在教学认识负数的过程中，学生由于惯性思维的影响，在比较负数和其他数的大小时，经常会出现错误，教师可以请数轴来帮忙。不管什么数，我们在数轴上都能找到一个唯一、确定的点与它相对应，根据数轴上的对应点，就可以很快地比较出数的大小关系。众所周知，数轴上面的数排列有这样的一个特点：越往左，数就越小;越往右，则反之。于是，教师为学生设计了这样的练习（如图2）。

在学生完成填空后，教师并没有满足，而是让学生在数轴上找几个小于1.5而大于-2.5的小数，旨在让学生通过数轴上的点与数的对应关系，强化对课堂中所学负数的认知，提升了学生思维的深刻性。

上述案例，在课堂教学的过程中，教师巧妙渗透数形对应的思想，将“看不见”的数转变为“看得见”的形，使抽象知识形象化，帮助学生更好地掌握了比较负数大小的方法，真正使学习方法的“根”扎得更深。

四、借助对应思想，探寻解题思路

分数应用题、百分数应用题是小学数学课堂的重要教学内容，也是学生学习的难点，且学生在解答问题的过程中，经常出现这样或者那样的错误。究其原因，是没有能够很好地把握数量和分率之间的对应关系，而出现了思维障碍。因此，在教学这类应用题时，教师应注重渗透量率对应的数学思想，让学生了解并掌握“单位1”这个整体的概念，使他们对题目的分析变得有迹可循，顺利得出正确的解题思路，获得基本的数学能力，真正让学生成为学习的主体！

教学这样一道分数应用题：“水果店运来一车苹果，第一天卖出了这车苹果的1/4，第二天卖出了这车苹果的2/5多40箱，第三天卖完剩下的170箱。这车苹果共有多少箱？”显然，这道题目的难度较大，学生想直接解答，是一件比较困难的事情。要想顺利解答这道题目，学生首先应找出具体的数量与对应的分率。于是教师引导学生对题目进行了分析和交流：①这车苹果的总箱数是单位“1”;②要求这车苹果的总箱数，也就是求“单位1”;③第一天卖出的箱数对应“1/4”，而第二天卖出的箱数对应的不是“2/5”，因为还多40箱。为了让学生更好地找出量率对应的关系，教师引导学生画出线段图分析：

学生看图后，恍然大悟，单独找40箱和170箱的对应分率不好找，但透过线段图可以看出，箱数（40+170）与分率1-1/4-2/5相对应，于是列出算式：（40+170）÷1-1/4-2/5=600（箱），得出了正确的结果。

上述案例，在学生苦于无法形成解题思路时，教师适时地融入量率对应的思想，让学生轻松地找到题目中量率与分率的对应关系，形成正确的解题方法，轻松地得出了正确的结论，从而提升了学生的思维品质，达到化繁为简、化难为易的目的。

总之，对应思想凝结着人类智慧的结晶，对学生思维能力的发展、数学魅力的体验有着不可替代的启迪作用。在以后的课堂教学中，教师应注重对应思想的渗透，将抽象问题直观化，复杂问题简单化，使学生找到更加自然、更加具有艺术性的解题策略，不断提升他们的数学综合素养，“悦”见思维的柳暗花明，真正让小学数学课堂充满生命的活力。