数学建模在初中数学教学中的实践应用

朱玉杰

摘  要：数学建模应当是在单元视角下连续的、不断完善的、由学生自主探索“识模—建模—解模—破模”的数学抽象过程. 学生是数学建模的主导者，而教师只是引导者. 在数学建模过程中，数学模型的形成、扩建和完善应尽量由学生自主或合作探究完成，而非教师强行灌输. 文章选取沪教版《九年义务教育课本·数学》九年级第一学期“25.4 解直角三角形的应用”的部分教学环节来阐述数学建模的课堂生成过程，以及从单元教学、学习进程、学科德育三个视角阐述数学建模在日常教学中的作用.

关键词：数学建模;单元视角;学习进程;学科德育

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识和数学方法构建模型解决问题的素养. 数学建模是应用数学知识解决实際问题的基本手段，其本质是应用能力，即在解决生活实际问题时，用数学眼光去发现问题，用数学表达去描述问题，用数学思维去解决问题. 数学建模建立了数学与生活、数学与其他学科之间的联系，它不仅有助于学生形成对知识体系完整的认识，而且有利于提高学生运用知识解决综合问题的能力.

在日常教学过程中，一线教师往往忽视数学建模的实际应用与育人价值，亦或者过于关注数学模型的应用而忽略了数学模型的构建过程及对数学模型的本质理解，导致学生心中无“模”或只有“模”的表征，而不理解“模”的本质.

笔者曾在线分享过数学建模在沪教版《九年义务教育课本·数学》九年级第一学期“25.4 解直角三角形的应用”这一单元教学的实际应用与思考，现选取部分教学环节整理成文，与同行交流.

一、教学环节及分析

1. 复习回顾，模型初识

师：同学们，我们已经学习了直角三角形的各元素之间的关系，哪位同学可以整理下它们之间的关系？

生1：（如图1）边边关系：[a2+b2=c2]（勾股定理）;角角关系：[∠A+∠B=90°]（两锐角互余）;边角关系：[sinA=ac，cosA=bc，tanA=ab，cotA=ba]（锐角的三角比）.

师：至少知道直角三角形中的哪些元素，即可实现解直角三角形？

生2：已知一边一角，或者两边.

师：今天我们将利用解直角三角形的知识解决一些生活实际问题.

……

【评析】锐角的三角比建立了直角三角形的边角关系，是解直角三角形至关重要的一环. 通过复习直角三角形各元素之间的关系，帮助学生完善直角三角形知识体系，通过分析解直角三角形的条件要求，初步构建解直角三角形的数学模型. 从单元视角考虑，梳理解直角三角形的知识，是为构建基础模型解决生活应用问题而服务，起到承上启下的作用.

2. 设置情境，模型扩建

（1）教学片断1.

师：现需要测量学校旗杆的高度，目前可以使用的工具有：高度为1.5米的测角仪（可测旗杆顶端仰角或底端俯角），一卷皮尺，请各小组成员，绘制基本图形，并设计测量方案.

生3：如图2，将测角仪（AB）放置距旗杆（CD）一定距离处，利用皮尺测量距离[BC]为a米，利用测角仪测量旗杆顶端的仰角[α]即可. 则旗杆CD的高度为[1.5+atanα]米.

师：生3的方案中涉及了哪些数学知识？

生4：已知一角一边求解直角三角形中的其他元素.

师：还有其他测量方案吗？

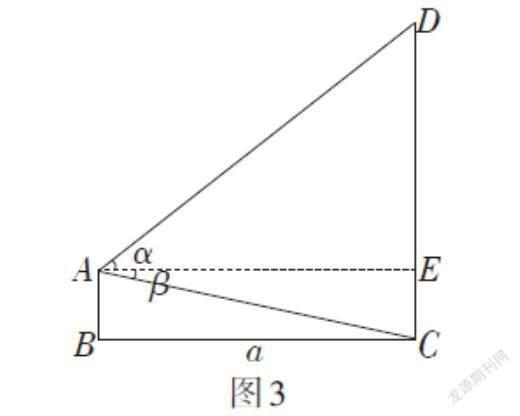
生5：在生3方案的前提下，如图3，再测量旗杆底端的俯角[β]即可. 则旗杆CD的高度为[atanα+atanβ]米.我们小组的设计，在将测角仪放置在适当高度的条件下也可以实施，且无需测量测角仪距地面的高度.

师：生5的方案中涉及了哪些数学知识？

生6：同样是已知一角一边求解直角三角形中的其他元素. 只不过这次涉及了两个直角三角形.

师：在同样的条件下，能测量出东方明珠广播电视塔的高度吗？小组讨论，并给出理由.

生7：生3的方案和生5的方案理论上可行，但测角仪和东方明珠广播电视塔的高度相差太大，可能在测量仰角和俯角时会有困难，仰角过大，俯角过小，误差都会很大，且在测量过程中也会受到周边建筑的遮挡影响.

师：很好！在将数学知识应用于解决生活实际问题时，需考虑实际环境的限制.

生8：可以对生5的方案进行改进，把测角仪的位置抬高，放在另一座高楼的楼顶去测量东方明珠广播电视塔塔顶的仰角和塔底的俯角，这样既可以减少误差，也可以尽量避免遮挡物的干扰.

师：分析得很好，以小组为单位，利用所学知识测量我校1号教学楼的高度，并形成测量报告.

【评析】通过活动的不断推进，让学生体会如何利用解直角三角形的知识解决生活中的测高问题，并引导学生注意在利用数学知识解决生活中的问题时，需考虑实际环境的限制，让学生优化方案，对测量过程进行改进，使改进后的方案更符合实际测量需要. 学生以主人翁的姿态参与到实际测高设计活动中，使学生感受数学与现实生活的联系，提高学生将数学问题实际化的能力. 同时，注重数学模型的扩建过程，由解单直角三角形向解具有一定联系的双直角三角形模型过渡.

（2）教学片断2.

师：解直角三角形的知识还可以用于解决一些生活中的测距问题. 例如，在海岸线建造观测站，可测得周围海域的船只位于观测站的方向角，通过解直角三角形的知识可测得船只距离海岸线的最短距离.

如图4，在一条笔直的海岸线l上有相距20海里的A，B两个观测站，B观测站在A观测站的正东方向上，从A观测站测得船C在北偏东60°的方向上，从B观测站测得船C在北偏东30°方向上，此时船只正以每小时50海里的速度快速向海岸线靠近，问：这艘船最短需要多长时间可以到达海岸线？（[3]取1.7，结果保留一位小数.）

师：小组合作，解决上述问题，并思考涉及了哪些基本图形及数学知识？（解题过程略）

生9：涉及两个直角三角形，且两个直角三角形的一条直角边共边.

师：它和图3中的双直角三角形有何不同？

生10：图3中双直角三角形在共边的异侧，图4中的双直角三角形在共边的同侧.

师：这两种情况在解决问题的策略上有何相似之处？

生11：均是利用解直角三角形的知识，使三角形的边角之间建立联系，复杂问题可能还要引入未知数，借助方程思想解决.

师：很好！如图5，这就是解直角三角形在实际生活应用问题中的两种常见的模型.

师：小组合作，根据所学知识，仿照上述情况，设计一套检测汽车行驶速度的方案，并形成方案报告.

【评析】不考虑生活情境，问题中涉及的基本图形是由具有公共直角边的两个直角三角形拼接构成，属共边同侧双直角三角形. 通过双直角三角形的边角关系，设未知数，利用方程思想建立等量关系，解出相应的距离. 而题目特殊角度的设置产生了特殊的位置关系，即[△ABC]是等腰三角形，学生也可以利用这点简化计算的过程. 该问题的设计意图在于让学生体会解直角三角形及方向角在实际测距中的作用，使学生体会到数学知识的实用性和可操作性. 通过让学生自主去对比两种情况的区别与联系，体验数学模型的扩建过程.

3. 例题精选，模型拓展

例  如图6，在大楼AB的正前方有一斜坡CD，长为13米，坡度为[1∶2.4，] 高为DE. 在斜坡底的点C处测得楼顶B的仰角为64°，在斜坡顶的点D处测得楼顶B的仰角为45°，其中点A，C，E在同一直线上，求斜坡的高DE与大楼AB的高度.（参考数据：[sin64°≈0.9，] [tan64°≈2.3.]）

【評析】不考虑生活情境，此题涉及的基本图形是共边同侧双直角三角形中的一种变式图形，让学生体会较复杂的双直角三角形边角间的内在联系，抓住双直角三角形的共边（或共线边），在两直角三角形的各元素之间建立联系，传递关键信息，利用方程思想建立等量关系，从而解决问题. 通过双直角三角形的不断变式，使学生对解双直角三角形问题具有深刻的认识，通过对基础图形的认识，进一步完善数学建模，提高学生的解题能力和认知能力.

4. 资源整合，破模归源

通过对基本模型的分析与整合，结合生活实例（图7和图8分别为将生活中的台灯和投影仪融入数学问题中的图形），让学生感受模型的实际应用，探寻模型的本源，体会应用的本质，即生活中常见的三类角（仰俯角、方向角、坡角），这些数学概念的引入是为了解决生活问题时表述的准确性，其本质就是不同场景下的角. 对于应用而言，作为条件，提供直角三角形一个角的信息，搭配一边，即可实现解直角三角形. 而对基础模型的拓展与应用是多个直角三角形之间边角信息关系的相互传递，把握关键信息，建立恰当的等量关系，从而解决问题. 通过资源的整合，打破模型的束缚，揭示问题的本质.

二、总结反思

1. 从单元教学视角看数学建模

王尚志教授认为，教师要从课时中跳出来，进行单元教学设计与实施. 单元教学也并非对课时教学的否定，而是提出了更高的要求，它要求教师在课时教学过程中都要从单元的高度和整体性把握知识的前后联系. 而数学建模过程亦是如此，在日常课时的教学过程中，帮助学生用全局的、联系的眼光观察生活问题，从现实问题中抽象出数学模型，再通过类似生活问题的比较研究完善数学模型（图9），找到数学知识的依附点，使它们不再零散、孤立. 数学建模是一个连续的，在单元视角下不断完善的过程，而非一蹴而就. 本单元是从现实生活中抽象出直角三角形模型，通过构造直角三角形，利用边角关系解决生活中的问题（图10）. 而锐角的三角比的定义、性质和应用均是基于该目标下的建模过程. 以单元视角展开教学，可以使学生更深刻地领会模型思想.

2. 从学习进程视角看数学建模

教师应该整体设计、分步实施教学建模活动与数学探究活动，引导学生从类比、模仿到自主创新，从局部实施到整体构想. 在数学建模活动中，学生是建模的主导者，而教师只是引导者. 在数学建模过程中，数学模型的形成、扩建和完善应尽量由学生通过自主或合作探究完成，而非教师强行灌输，让学生经历“识模—建模—解模”的过程，对数学模型有自我认识和理解，并从中感悟模型背后问题的本质，最终达到“破模”的境界，而非只是识“模”的形式，不知“模”的本质. 过于依赖模型，只会局限学生思维的发展和解题能力的提升. 数学模型获得及提炼过程的价值远远超过运用它去机械性解题.

3. 从学科德育视角看数学建模

数学建模本质上是一个问题解决的过程，而问题应来源于日常生活、现实世界等多方面，因此要重视数学与现实生活的联系. 在学习评价中，不仅要关注学生会用数学模型解决简单的实际问题，而且还要关注学生学数学、用数学的意识和能力的提高，让学生亲身感受数学来源于生活、服务于生活的理念. 培养学生的数学价值观，用数学眼光去发现问题，用数学表达去描述问题，用数学思维去解决问题.

如何在教学中引导学生在单元视角下连续不断地、自主地探索“识模—建模—解模—破模”过程，让学生感受到数学理性的魅力，培养学生的数学观，需要教师不断地探索、思考、改进.

参考文献：

[1]中华人民共和国教育部制定. 普通高中数学课程标准（2017年版）[M]. 北京：人民教育出版社，2018.

[2]章建跃. 核心素养统领下的数学教育变革[J].数学通报，2017，56（4）：1-4.

[3]王尚志，胡凤娟. 数学教育的育人价值[J]. 人民教育，2018（13 / 14）：40-44.

[4]张玲玲. 为表达世界而建模：《指数函数》三次备课思考[J]. 数学通报，2019，58（8）：52-54.

[5]周龙虎，刘师妤. 对模型教学以及探求建模的一些思考[J]. 数学通报，2017，56（9）：30-34，54.