巧设问题 激发兴趣——“两角差的余弦公式”教学设计

管良梁

(安徽省合肥市第四中学,233000)

本节课是《普通高中课程标准实验教科书数学》人教A版必修4第三章“三角恒等变换”的3.1.1节“两角差的余弦公式”，属于新授课.本节内容是三角恒等变形的基础,是正弦线、余弦线和诱导公式等知识的延伸,也是两角和、差、倍、半角等公式的基础.

教学过程设计如下：

一、创设情境

问题1某城市的电视发射塔建在市郊的一座小山上.在地平面上有一点A,测得A，C两点间距离约为60米，从A观测电视发射塔的视角(∠CAD)约为45°，观测小山的视角(∠CAB)约为15°，求这座电视发射塔顶端D距离地面高度(如图1).

师:请应用已有的知识将电视塔的高度表示出来．

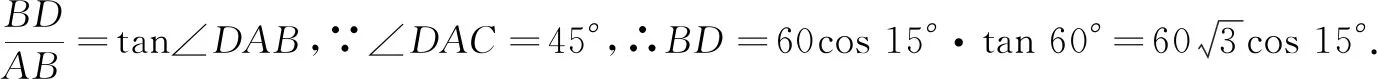
设计意图问题1是由《普通高中课程标准实验教科书》(数学)人教A版必修4第124页的问题改编而来的.由学生独立上黑板完成.这类问题学生在初中已经学习过,对学生而言是非常熟悉的问题.从熟悉的问题出发,对已知经验进行回顾,在回顾的过程中发现问题.

二、 探索尝试

问题2cos 15°=?

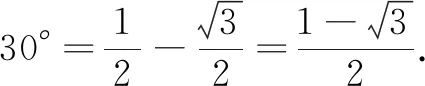
设计意图学生凭直觉容易犯cos(α-β)=cosα-cosβ这样的错误.通过教师提问,学生动笔计算发现，cos(α-β)=cosα-cosβ一般不成立.这样也可避免学生在以后的学习过程中犯同样的错误,同时激发学生的求知欲和探究的动力.

三、 探索新知

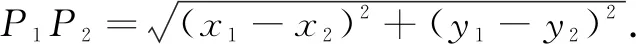
问题3如图2，若α≠β+2kπ,k∈Z，在平面直角坐标系中作单位圆,以x轴非负半轴为始边作角α,β, (α-β),它们的终边与单位圆O的交点分别为P1，A1，P,则P1，A1，P三点的坐标如何表示?

生:P1(cosα,sinα)，A1(cosβ,sinβ)，P(cos(α-β),sin(α-β)).

问题4如何将sin(α-β)，cos(α-β)，sinα，cosα，sinβ，cosβ这六者联系起来?

生:由圆的旋转对称性可知，弧P1A1等于弧PA，故有P1A1=PA.再由两点间距离公式推导出cos(α-β)=cosαcosβ+sinαsinβ.

师:当α=β+2kπ,k∈Z时,很容易证明上式.所以,对于任意角α，β有

cos(α-β)=cosαcosβ+sinαsinβ.(Cα-β)

引导学生试着应用公式解决例1遗留的问题.

问题5两角差的余弦公式有什么结构特点?

生:发现公式左边是差角的余弦,右边是单角同名三角函数值乘积之和.

设计意图通过教师的引导,激发学生自觉回顾三角函数和两点间的距离公式的相关知识,为公式的探索提供思路.通过带有指向性的问题,使学生意识到,代数问题几何化,几何问题代数化,培养学生自主探索和数形结合的能力;使学生体会和认识严格的推导过程，是获取数学结论的方法.由学生通过自身的努力得到结论,让学生在数学课上体验成功.

培养学生用自己的语言描述公式的结构特点的表达能力，加深对公式的印象,为下一步公式的应用打下坚实的基础.

四、例题讲解

例1(1)cos 50°cos 20°+sin 50°sin 20°的值为______;

(2)cos(-15°)的值为______;

(3)化简cos(α+45°)cosα+sin(α+45°)sinα=______.

设计意图例1是两角差的余弦公式的简单应用.通过本例帮助学生注意以下三点:

(1)在两角差的余弦公式中,α，β既可以是单角,也可以是复角;

(2)要注意诱导公式的应用;

(3)公式的应用具有灵活性,解题时要注意正向、逆向和变式形式的选择.

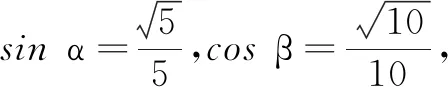
设计意图例2是利用三角函数值求角，即给值求角问题.通过本例使得学生掌握解决这类问题的步骤:(1)求角的某一三角函数值;(2)确定角所在的范围;(3)根据角的范围写出所求角.

五、 课堂小结

师:通过这节课的学习,你都有哪些收获呢?

生:(1)了解了两角差余弦公式的推导过程；

(2) 掌握了两角差余弦公式及其应用.

问题6两角差的余弦公式的应用需要注意什么?

生:注意公式的正向、逆向和变式的选择以及角的范围.

设计意图加深学生的记忆,注意:(1)两角差的余弦公式的结构特点；(2)忽略角的范围而产生增根.

本节课从学生熟悉的问题出发,在应用已知问题解决未知问题的过程中发现新的问题,激发学生学习的兴趣.巧妙设置六个问题，引导学生积极主动分析问题,寻求解决问题的途径和方法,在老师的帮助下推导出两角差的余弦公式,最后应用公式解决问题.在教学的过程中，让学生体验数学发现和创造的历程,发展创新意识.