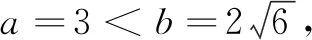加强学法指导 培养学习习惯

石 鹏

(江苏省石庄高级中学，226531)

良好的习惯是学生的良师益友,会陪伴学生的终身．如何培养数学学习习惯,笔者认为可以从以下几个方面进行培养．

一、指导学生预习方法

1.指导新授课的预习,享受知识的生成过程

可以先创设一种学生比较熟悉、直观、容易接受的探究活动,让学生通过活动的引领,增加感性体验.给学生一定的时间自主探究,合作讨论,再全班交流,这样不仅能体现概念的产生过程,让学生在体验中建构新知识,享受知识的生成过程．

案例1在苏教版必修4“平面向量”第一节课“向量的概念及表示”教学时,可布置学生阅读课本第59页到61页, 并完成下列活动．

活动1:向量的定义是什么?向量、数量、矢量有什么区别?通过举例来进行说明;

活动2:向量的表示方法有哪些？与矢量的表示有何异同？

活动3:零向量、单位向量如何描述？如何表示?

活动4:向量与向量之间的关系有哪些(几何和代数)?向量之间可比较大小吗?若能说明如何比较,若不能请说明理由,并指出向量的哪一方面可以比较大小?

评注设置四个活动主要是让学生通过对课本的阅读,了解新课的知识点有哪些？思考新课的重点和难点是什么？自己还有什么不能理解,那些需要教师点拨的;结合学生的认知水平和预习能力，布置具体可行的预习作业, 让学生了解新课中的知识点.

2.指导知识点的预习,提升知识应用的能力

在课堂讲义中增加了课前预习题一栏,用简单的题目倒逼学生去预习新课,让学生通过题目知道这一节课概念、公式、定理有哪些？思想方法和思维手段又有哪些？自己的知识和方法的缺陷又有哪些？等等．

案例2苏教版必修5中“解三角形”第二节“余弦定理”可以添加以下预习题:

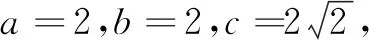
(2)在∆ABC中,若a∶b∶c=2∶3∶4,则cosC=______.

(3)在∆ABC中,已知(a+b+c)(b+c-a)=3bc,那么角A=______.

(4)在∆ABC中,已知c=2acosB,那么∆ABC的形状为______.

评注第(1)小题知道了三条边求角,引导学生回忆余弦定理公式;第(2)小题由于知道边的比,设出合理的参数,进一步强化余弦定理的应用;第(3)题对等式进行合理的变形,需灵活运用余弦定理;第(4)小题让学生体验用正弦定理或者余弦定理来判断三角形的形状,体验两者的运算量、运算技巧、运算节点、运算路径的异同．

3.指导章节课复习课的预习,提升学生学习的效率

在对一章节进行复习课时，可以通过制作活动单,或者列出表格，让学生回归知识框架,在学生有了基本概念、基本公式的知识准备前提下,再开展这一章节的复习．

案例3在苏教版必修2“立体几何初步”这一章复习时,可以列出下列框图．

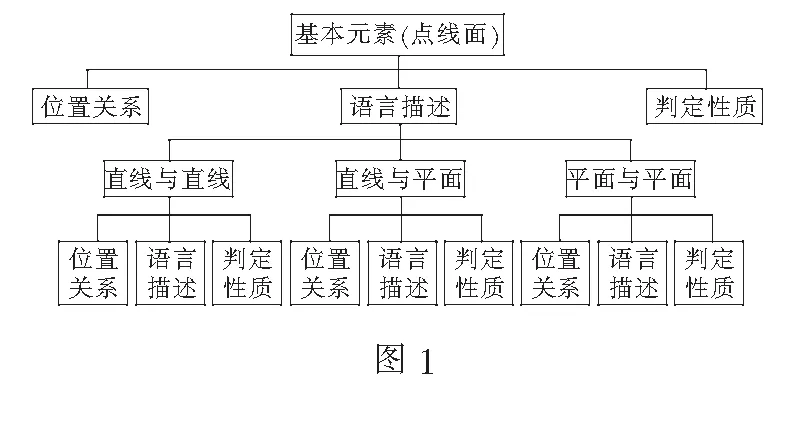
评注通过以上框图,学生能够一目了然知道立体几何这一节的直线、平面的定义、定理、公理有哪些？通过学生自己的回忆,了解对哪些知识已经掌握,对哪些知识还是有所欠缺.学生可以通过查看自己的课堂笔记以及课本,查找自己知识的缺陷,弥补知识的盲点.

二、培养学生自主思考习惯

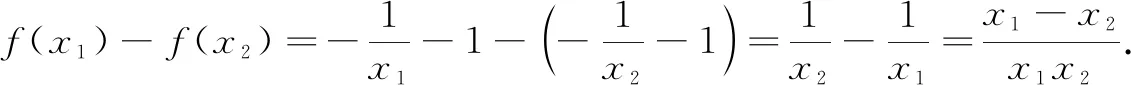
评注这是苏教版的必修4的“单调性”这一节中的例题,学生读完题目,首先思考证明的工具(理论)是什么?分析得知只能根据函数的单调性的定义进行,那就需要取值x1,x2,然后比较f(x1),f(x2)值的大小,即可．学生证明结束后,教师进行适当的点评,更应让学生自主归纳、自主提炼出证明函数单调性的步骤有取值、作差、变形、判断、结论这样五步．

三、指导学后反思,错后反思

1.对所学的概念、定理、性质进行反思

由于高中数学的概念、定理、性质具有高度的抽象性和概括性,学生比较难理解,并且高中数学课堂容量较大,许多学生走马观花,对概念、定理、性质仅仅停留在“只知其表,不知其里”．

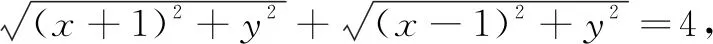
2.对题型进行反思

在练习训练的同时,要针对同一类问题,不同的题型,采用不同处理手段进行处理．

案例6已知等比数列{an}的前n项和Sn=m·2n-1,试求参数m的值．

解当n=1时,a1=S1=2m-1；当n≥2时,an=Sn-Sn-1=m·2n-1-m·2n-1+1=m·2n-1.所以n=1时,m·20=2m-1,解得m=1,此时an=2n-1.

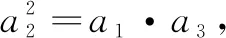
3.对解题方法进行反思

在学生独立自主完成相关作业时,应鼓励学生用多种方法解决一道题目,乃至让学生达到“多题归一”的境界．

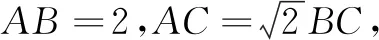
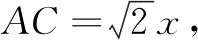
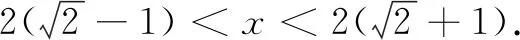
在三角形∆ABC中,由余弦定理得

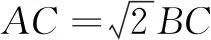
4.对结果进行反思

许多学生解完题目后,不对结果进一步检查和反思,长此以往,分析问题和解决问题的能力也得不到提高．