基于深度学习观的信息化教学实践

朱宝平 舒大展

(安徽省亳州市第一中学，236000)

《教育信息化十年发展规划(2011——2020 年)》明确提出了“推进信息技术与教学融合，培养学生信息化环境下的学习能力”的发展任务,这就要求我们反思如何利用信息技术促进学生多维度的发展,而深度学习理论将发挥重要的作用,本文对此进行探索．

一、深度学习观的内涵和特征

2005年,黎加厚教授指出:深度学习是指在理解学习的基础上,学习者能够批判性地学习新的思想和事实,并将它们融入原有的认知结构中, 能够在众多思想间进行联系,并能够将已有的知识迁移到新的情境中,作出决策和解决问题的学习[1].深度学习观下信息化教学有如下特征:学生学习的认知过程逐层抽象,计算机能够把抽象的知识采用形象具体的形式进行表达;深度学习的反思为逐步加深理解,批判性思维,自我反思,互联网能让学习者分享整合他们的对于知识的认知,能够进行视觉、听觉相结合的反思模式,通过合作学习,共同提高;深度学习的学习形态为深层加工、深度理解及长期保持,知识建构、迁移应用及问题解决,工具软件固有特征有利于深度学习的深层加工、数学建模以及迁移思维的发展．

二、基于深度学习观的信息化教学案例

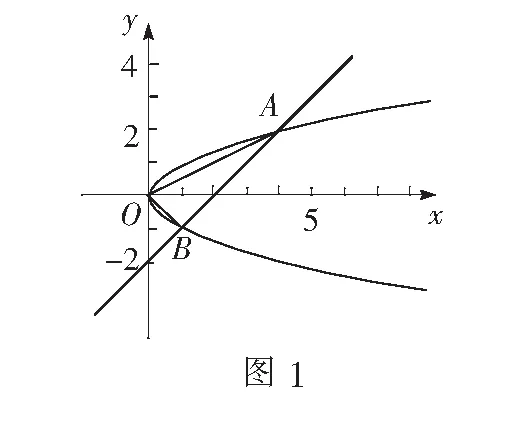
教学案例如图1，已知直线y=x-2与抛物线y2=2x相交于A，B两点,求证:OA⊥OB.

Q1:这道题考查什么知识点?——解析几何中“直线与抛物线”的位置关系．

Q2:直线和抛物线有哪些位置关系?——相离、相交(特殊的相交)和相切(利用几何画板演示,直线转动时与抛物线的交点不同)．

Q3:解析几何的方法是什么?——运用代数的方法解决几何问题,建立直角坐标系．

Q4:本题要解决什么问题呢?——两条直线垂直的证明．

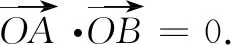
Q6:用哪一种方法更好呢?——注意在直角坐标系中,点O的坐标已知,是否要将A，B两点的坐标求出来呢?——A，B两点的坐标可能不好表示,可以采取“设而不求”.无论是斜率方法还是向量的数量积的方法,最终都会转化为A(x1,y1),B(x2,y2),x1x2+y1y2=0的形式.不妨采用向量法,已知直线和抛物线方程,联立就可以证明．

Q7:具体怎么做呢?

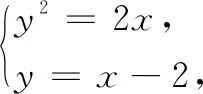
y1y2=(x1-2)(x2-2)=x1x2-2(x1+x2)+4=-4.

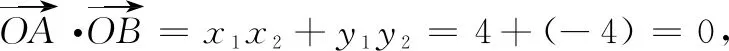
Q8:根据题中已知条件,能不能将它拓展为一个结论呢?

直线y=k(x-2p)与抛物线y2=2px(p>0)相交于A、B两点,求证:OA⊥OB——我们用几何画板来演示如下(如图2).

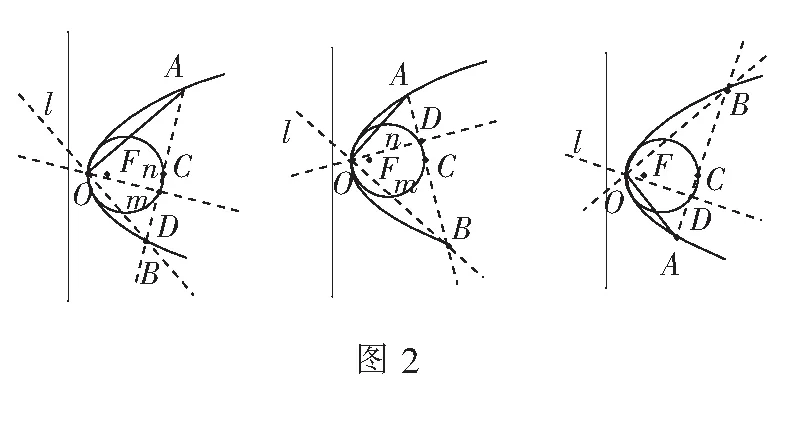
Q9:不难发现,拖动点A,始终有OA⊥OB.如何进行证明呢?

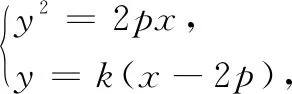
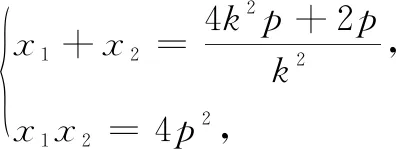
x1x2+y1y2=x1x2+k(x1-2p)k(x2-2p)

=x1x2+k2(x1x2-2p(x1+x2)+4p2)

=x1x2+k2x1x2-2pk2(x1+x2)+4k2p2

=4p2-4k2p2-4p2+4p2k2=0.

综上,OA⊥OB.

Q10:在几何画板演示的过程中,中间出现了圆的形态,这里过点O作OD⊥AB于点D,试试看点D的轨迹方程是什么呢?

利用软件(比如几何画板)进行动态演示,会使得问题更加形象化,进而进行证明,这也符合学生的认知规律,从形象到抽象,由具体到一般的规律.这对于找到一般规律,进行构造拓展是大有裨益的.从深层次理解应用数学知识,可以看出,信息化在某种程度上明确了数学问题深度学习的形象化,为问题的一般化研究提供了动态的变化．

三、关于深度学习和信息化的几点思考

信息化给深度学习带来极大的便利,使得数学过程可视化、形象化.信息技术能提高深度学习的效率,主要体现在以下方面.

1. 智能伙伴的作用,工具软件的特征能促进深度学习的发生、发展和延拓．

软件工具具有思维的具体化、动态化和可视性．如概念图、语义网络、数据库等，可以促进学习者思维和认知结构的重新组合,促进有效的深度学习．又如电子报表可以达到预测的目的,加上对数据的数学处理,可以重新进行预算,大大节省了盲目性带来的精力的损失和资源的浪费．

2. 高阶思维的投入有利于学生深度思维的发展

高阶思维能力包含基本思维、批判性思维和创造性思维等三大能力,学习者在使用认知工具时,必须通过进行复杂的思维解决问题和表征知识,包括问题求解、设计产品或观点和做出决策．如在使用PPT等多媒体完成活动时,学习者必须投入自己的见解，自主参与到设计过程中进行设计、阐述自己的观点和意见,进而提高深度学习的能力．又如几何画板、物理实验室等信息技术工具,学生可以进行几何图形内在联系的探究或者物理规律的探索,通过软件观察现象、测量、数据收集、撰写实验报告和反思,最终可以探究、验证数学或物理规律．

3. 学生的深度学习需要教师提升信息化深度学习的策略

首先确定目标,深度学习就是要发展高阶思维能力．深度学习是指应用、分析、综合、评价,是高阶思维能力的体现,教学目标决不能仅仅停留在知道、领会的层次,要深入地领会教材,除了注重学生的基本知识和基本技能外,更要注重分析、创造性思维的应用．

其次合理设置知识建构的问题:将教学元素进行“信息组块”设计,使得学习者将创新纳入到原有的认知体系中去．另外还要思考哪些知识是容易的,哪些知识是对学习者知识构建有益处的,能够让学生自由发挥,实现头脑风暴,凝聚集体的智慧．

综上，深度学习是当代学习领域的新概念,在数学问题的研究、探索上发挥着重要的作用.通过教师设置问题串,引导学生积极思考,勇于探索,提高了解决问题的能力,有利于找到问题的内在规律,从本质上解决问题,真正做到举一反三、触类旁通．而信息化为深度学习提供了技术工具,使得复杂的问题可视化、形象化．而信息化教学和深度学习是将信息技术和学科知识融合,值得从理论和实践层次进行进一步的探究．