例谈高三数学复习的有效策略

刘白丽

(广东省广州市第七十五中学，510000)

课程改革的基本理念是在教学过程中促进学生的自我发展,使其学习过程具有主动性、积极性、探究性,实现能力的提高,形成科学素养[1]．高三学生面对的是高中数学所有知识的总复习与高考,因此高三复习中课堂教学有效性问题是一个很值得研究的课题．那么如何提高实效性呢?

一、在自主学习中完善基础知识

数学基础知识包括基本概念,公式,定理等,是学生数学认知水平发展的重要学习载体,因此牢固掌握并灵活应用数学基础知识，是提高解题能力的前提．

高三复习首先就是要帮助学生建构完善的知识结构,而传统教学中，无论是先复习基础知识再做题，还是以训练题为载体复习基础知识,总感觉是教师在梳理，而不是学生在记忆,复习效果很不好[2].这些知识学生已经在高一、高二系统学习过,对绝大多数学生来说还是很容易梳理的,所以应把带领学生复习基础知识的做法改为领而不带,变教师梳理为学生梳理,让学生自己编织还没有完善的知识结构,再在课堂上与同学、教师交流的过程中进一步完善．

案例1在复习“直线方程”这一章时,基础知识不多,难度也不大,所以前一天布置学生完成学案,并以学习小组为单位对本章知识点梳理归类,上课时随机选出一个小组展示其成果,然后其他小组补充,最后归纳出本章考察的主要知识点有直线的斜率、倾斜角、直线方程的五种形式．所有要点展示出来后,再让学生结合要点叙述其具体含义,检查学生的掌握程度,然后结合学案提问:

(1)解决斜率问题要注意哪些?

(2)直线的斜率为tanα,此直线的倾斜角为α吗,解决倾斜角问题要注意什么?

(3)直线方程的几种形式要注意什么?

问题(1)、(2)让学生理解直线倾斜角和斜率的关系以及自身特点,问题(3)提醒学生在使用直线方程时要考虑各个形式的适用范围,要注意讨论特殊情况． 这些问题通过老师的讲授未必能保证学生牢固掌握,但是通过调整顺序,把学生推至台前,将他们的思维展开,提升他们的参与水平,改变接受记忆模仿的教学方式,就会变被动为主动.学生通过自己主动复习、归纳,对概念,公式等基础性知识有了更深入的理解,站得更高,看得更远,效果也会更好．

二、在变式训练中强化解题能力

哈尔莫斯说:“数学的真正组成部分应该是问题和解,解题才是数学的心脏．”波利亚也称:掌握数学就意味着善于解题[3]．因此,解题教学是高三数学总复习的重要组成部分．解题教学的质量直接决定总复习的效果,而精选例题,重视变式是提高解题教学水平的有效途径．

案例2在复习“函数性质的应用”这一节时,可选择一道教材改编题引入复习.

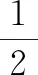
此题虽然比较简单,但是复习导入选择的题目越基础、越经典,效果就越好,就越能真正实现由浅入深.在引导学生运用分离变量法将问题转化为求函数最值后,启发学生借助函数的图象求解,并以此为基础,让学生对下面的变式训练展开探究.

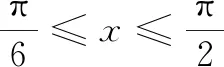
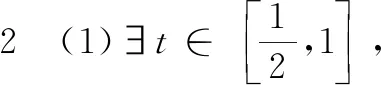
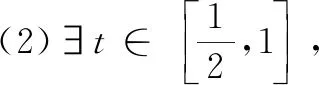
变式3已知两个函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x(k为实数).

(1)对∀x∈[-3,3],都有f(x)≤g(x)成立,求k的取值范围;

(2)若∃x∈[-3,3],使得f(x)≤g(x)成立,求k的取值范围．

变式4已知两个函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x(k为实数).

(1)若∀x1,x2∈[-3,3],都有f(x1)≤g(x2)成立,求k的取值范围;

(2)若对∀x1∈[-3,3],∃x2∈[-3,3],使得f(x1)≤g(x2)成立,求k的取值范围．

在解变式3时,有些学生提出利用f(x)max≤g(x)min来处理.在组织学生对这种错误方法的探讨中,自然地引出了变式4的解决方法.而教师也通过这一道例题的变式探究,让学生多方面、多角度进行思考和探索,做到一题多解，多题一解,不断积累并总结源于教材的解题经验和方法．

课堂上多给学生时间去探索、讨论,在变中突出不变的规律,讲一题，通一类，会一片,从而让学生深刻认识到恒成立和存在性问题,均可和函数的值域联系起来.如此一来,通过潜移默化,使学生融会贯通，牢固掌握知识．

三、在开放探究中提升思维能力

数学教学是思维的教学.解题过程也是思维过程,是一个把问题和知识、方法联系起来进行思考、分析、探索的过程,是教师引导学生“用自己的头脑亲自获得知识的再发现过程”.高三复习课更应如此,要把培养学生的思维能力作为首要任务[4]．高三的教学是复习,但不是重复,要讲究新鲜感,学生做过的学案若逐题讲解,或者学生已会的习题再重复讲授,不仅不会“熟能生巧”,相反会“熟能生厌”，“熟能生笨”[5],因此对练习题重组、开放是改变传统复习课的有效方法,是提高学生思维能力的有效措施．

案例3在“平面向量的运算”复习课中,在完成知识梳理后,给出了以下两道开放题.

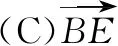
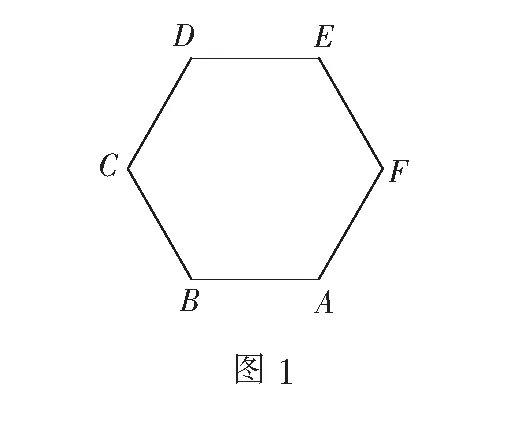
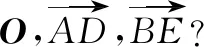
(2)已知a=(1,2),请通过添加条件编拟一道习题,并给出解答．

这两道都是开放题,因为答案不唯一,学生们的积极性很高,特别是题(2),大家设计出了如下题目.

(i)b=(2,3),求夹角的余弦值(或投影,或|a+2b|)；

(ii)|b|=1,a∥b(或a⊥b),求b的坐标；

(iii)|b|=1,a·b=3(或a⊥b),求|a+2b|；

(iv)b=(1,m),a,b夹角是钝角,求m的取值范围，等等.

教师在充分肯定学生的成果后,也适时展示学生没有提出、但需要强调的题目．这些题目既包含了平面向量专题的基本题型,也蕴含了解决平面向量问题的最基础的技能和方法,教师也在这种开放的教学环境中,轻松实现教学目标．

可以看到,通过开放题的教学,引导学生从多方面、多层次探究、分析问题,使学生产生尽可能多、尽可能新的独创想法,达到沟通不同部分的数学知识和方法的目的．在开放的师生互动中,培养学生的创新意识和探究能力,使他们的思维更具有灵活性、严谨性和创造性．

四、在纠错反思中走向成功

《学记》有云:“学者有四失,教者必知之．知其心,然后能救其失也,教也者,长善而救其失者也”[6].学生在数学学习过程中出现错误属正常现象,但如何做到“长善救失”就显得至关重要了．教师应把学生的错误当作课堂教学的教育资源,通过评析错误让学生认知更深刻,理解更透彻,教学有效性就会更显著．

案例4在复习“应用基本不等式求最值”一节中,用这样一道练习题:

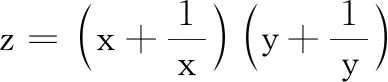
在预设中估计学生会在处理方法上出现一些错误,先让学生练习,在巡视的过程中发现典型错误,并把这些问题展示出来:

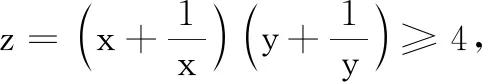
在展示的过程中,与学生共同反思:这两种解法对吗?若错,错在哪里?因为是学生自己犯的错误,大家纠错的积极性很高,很快就找到了问题所在.

从而进一步深化基本不等式使用的条件“一正二定三相等”,再由错解2引导学生发现在基本不等式无法使用的情况下,就可以考虑通过化归与转化的数学思想,利用函数的单调性求解,进而得出正确的解法:

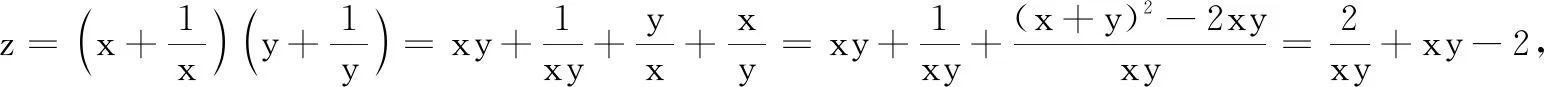
上述案例中,通过学生的错误,暴露学生思维过程和方法中的缺陷,不仅极大地调动了学生的积极性,将学生在参与活动过程中生成的信息转化为有效的教学资源,并得到了有效的内化,使复习更为高效．学生也在对错误的反思中吸取教训,从自身所犯错误中学习,学会突破障碍,学会调整思维方向,从错误走向正确,从失败走向成功．