“两角和与差的正弦、余弦”的教学实践与反思

王慧凯

(山东省桓台县渔洋中学，256400)

《普通高中数学课程标准》(2017年版)指出:高中数学课程应以学生发展为本,落实立德树人根本任务,培育科学精神和创新意义,提升数学核心素养.数学核心素养是落实课程目标的主要途径,包括数学抽象、逻辑推理、数学建模、直观想象、数据分析、数学运算.这些核心素养既相对独立又相互交融,是一个有机的整体.如何在教学中融入核心素养,将新课标落实到实处?笔者在教学中做了一些探索.现摘取“两角和与差的正弦、余弦”教学片段即推导公式环节,抛砖引玉,不妥之处恳请斧正.

一. 教材及学情分析

本节是人教A版必修第二册5.5.1“两角和与差的正弦、余弦和正切公式”第二课时，是在本章第三节变换对象只有一个角的三角函数式基础上拓展为包含两个角的三角函数式.两角差的余弦公式是第一课时内容,此公式既是前面诱导公式的进一步扩充,又是后面学习二倍角公式的前提与依据,是三角恒等变换的基础,具有很强的工具性.本课时是第一课时的延续,将以两角差的余弦公式为基础,联系诱导公式,推导其它公式.

学生已掌握了诱导公式及两角差的余弦公式,对于推导公式有一定经验.本课时将从学生认知与思维构建的角度,帮助学生充分认识知识、方法间的联系,采取由特殊到一般、由具体到抽象的方式推导公式.

二、 课堂实录

1. 温故知新

师:上一节课,我们推导了两角差的余弦公式,借助公式可以将有些非特殊角转化为两个特殊角的差来求值.能求cos 75°吗?

生2:将75°拆分成90°-15°,再运用公式得cos 75°=cos(90°-15°)=cos 90°cos 15°+sin 90°sin 15°=sin 15°.一方面15°不是特殊角无法直接求值,另一方面仅有两角差的余弦公式,求两角差的正弦无法进行.

生3:可以将75°分成30°+45°.于是cos 75°=cos(30°+45°),转化为两角和的余弦后,不能继续.

师:现在我们来探究同学提出的问题.

设计意图通过已知引发未知,体现知识间的联系,激发学生探究兴趣,培养学生知识迁移能力.同时将问题设置成开放性问题,激发学生发言的欲望,培养学生的发散思维,落实数学逻辑推理素养.

2.同宗溯源

师:先来看cos(30°+45°),将之抽象为任意角α，β，即cos(α+β).

生:这与两角差的余弦公式Cα-β仅仅差一个符号.考虑到α+β与α-β的联系α+β=α-(-β), 可运用两角差的余弦公式及诱导公式，于是有

cos(α+β)=cos[α-(-β)]

=cosαcos(-β)+sinαsin(-β).

生2:直接在两角差的余弦公式中用-β代替β也可以推导出刚才的结果.

(过程略)

设计意图让学生经历由特殊到一般的过程,体现数学的化归思想;在探索运算思路的过程中,培养学生知识迁移能力,落实数学逻辑推理素养、数学抽象素养和数学运算素养.

3.近水楼台

师:请同学们求sin 15°的值.

生:sin 15°=cos(90°-15°)=cos 75°,然后用两角和的余弦公式即可求之.

师:sin 15°=cos 75°体现了角的正弦与余弦的互化,与前面我们学习的诱导公式相呼应.

同时sin 15°=sin(45°-30°).将45°、30°抽象为任意角α，β即sin(α-β).请大家自行推导出两角和与差的正弦公式.

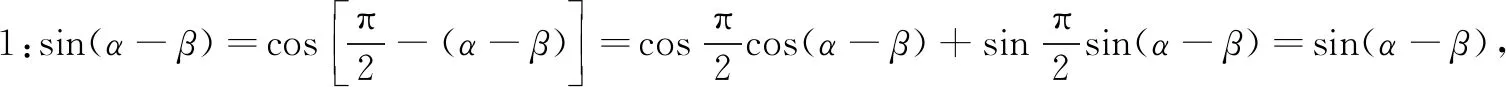
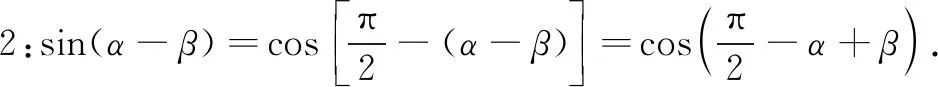
师:请同学们集思广益来帮助这两位同学.

师:请同学们运用以上两种思路推导公式.

=sinαcosβ-cosαsinβ.

生2:sin(α-β)

=-sinβcosα+cosβsinα

=sinαcosβ-cosαsinβ.

师:以上我们推导出两角差的正弦公式,同学们能运用所学的知识推导两角和的正弦公式吗?

(学生推导过程略)

师:公式Sα±β有怎样的结构特点?

生:与公式Cα±β的结构特点相似.

师:我们可以类比公式Cα±β用口诀“正余余正符号同”来帮助记忆.

设计意图学生在经历正弦化余弦,正角化负角的过程中,体会数学转化思想,同时培养学生分析问题、解决问题的能力,培养学生灵活性、批判性的思维品质,落实数学逻辑推理素养.

4. 和差家谱

师:以上我们推导出两角和与差的正弦、余弦公式,它们之间存在怎样的关系呢?

生:可以用这样一个示意图来表述推导四个公式的过程(如图1).

设计意图通过此环节,引导学生理清公式之间的关系,沟通知识之间的联系,既能纵向追溯教材知识体系的认知与梳理,也能横向加强知识之间的联系,培养学生的数学整体观、思维的灵活性和知识迁移能力,落实数学逻辑推理素养.

三、教学反思

1.反思引入

章建跃先生认为:从数学知识发生发展过程的合理性,学生思维过程的合理性上加强思考,这是落实数学学科素养的关键点.在教学设计之初，考虑到学生已经推导过两角差的余弦公式,在公式应用中已经认识到三角函数式的特征,体会到三角恒等变换的特点.因此,学生联系已经学过的三角函数知识探索有关三角函数的问题是很自然的.基于以上思考,在教学设计时没有选择教学情境引入,而是通过已有知识难以解决或无法解决新问题,引发学生探索新知识的欲望,既温习前面学习的内容,又体现出新知与旧知的联系.避免了“有些课堂引入刻意联系实际,不够自然,或者引入高于学生的认知水平,学生不能建立有效的数学模型”.

2.反思过程

教材不仅重视对推出的公式的理解、应用,而且还重视推导过程的教育功能.因此,本节课教学采用自主探究的方式,让学生经历疑惑——探索——解决的过程,培养学生的数学学科素养.

在公式推导过程中,始终把对照、比较有关的三角函数式,认清其区别,寻找其联系和联系的途径作为思维的起点,培养学生逻辑推理数学核心素养.例如,比较cos(α+β)与cos(α-β)，发现它们都是角的余弦,只是和差不同,但它们不论从运算的角度还是换元的角度看都有内在联系,根据这种联系可以实现从Cα-β到Cα+β的推理过程.再如,比较sin(α-β)与cos(α-β),它们包含的角相同,但函数名称不同,如何建立二者之间的联系?显然,诱导公式可以实现同角正弦余弦转化,根据此公式可以由Cα-β推导出Sα-β.

同样,将特殊角30°，45°抽象为任意角α，β的过程,体现了特殊到一般的数学思想,也落实了数学抽象核心素养.在求cos 75°，sin 15°的过程中,学生运用公式及特殊角的正弦、余弦值计算,落实了数学运算核心素养.

总之,课程标准是教学设计的依据,核心素养是教学的目标.教师在教学设计前,应先充分了解学生的知识能力和思维特点,在此基础上精心设计教学过程,让学生在高效的学习过程中提升数学思维能力和核心素养.