例说经典例题在复习课中的教学价值

李恩斌 王祥熙

(四川省巴中市第二中学，636013)

本文通过对一道经典例题(北京2020届高考模拟试卷(一)第16题)的分析、解法探究和变式练习，谈谈在高三教学中如何发挥经典例题在复习中的教学价值.

题目(北京2020届高考模拟试卷(一)第16题)在∆ABC中，2AB=3AC，AD是∠BAC的角平分线，设AD=mAC,则实数m的取值范围.

一、一题多解，让问题由点构成线

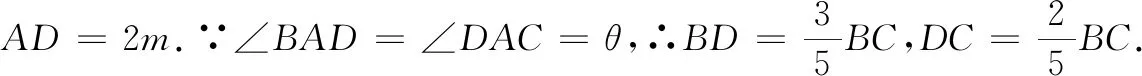
解法1(等面积法)

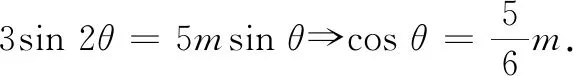
点评等面积法是一种重要的解决问题的方法.利用等面积法，可以简捷思路，明朗图形之间的关系.

解法2(向量法)

点评向量法实质上是一个使几何结构代数化的过程，它是沟通代数、三角、几何等内容的桥梁之一.向量的三角形法则、向量的数量积是架起桥梁的基石.

解法3(应用余弦定理)

在∆ABD中，

BD2=AB2+AD2

-2AB·ADcosθ.

①

在∆ADC中，

DC2=AC2+AD2

-2AC·ADcosθ.

②

点评余弦定理将三角形的边和角有机地联系起来，是解三角形有关问题的重要工具.

解法4(应用余弦定理)

如图2，设∠ADB=α,∠ADC=π-α,BD=3x,CD=2x,AD=2m.

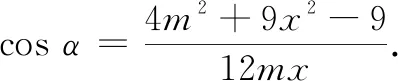
①

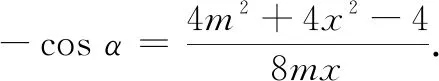
②

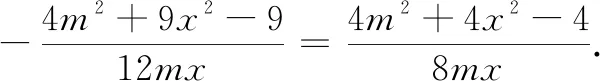
②

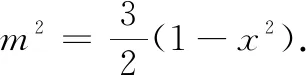
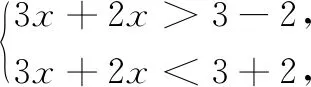
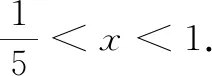
点评此题仍应用了余弦定理，但思考的角度不同，利用余弦定理分别表达互补角，建立等量关系是常用的方法，构成三角形三边条件的限定是隐含条件，要善于挖掘.

解法5(共圆法)

如图3，由外角平分线定理得(∠CAF为∆BAC的外角，AE平分∠CAF，可设∠CAE=∠EAF=α)，不妨设BD=3x,DC=2x,CE=y.

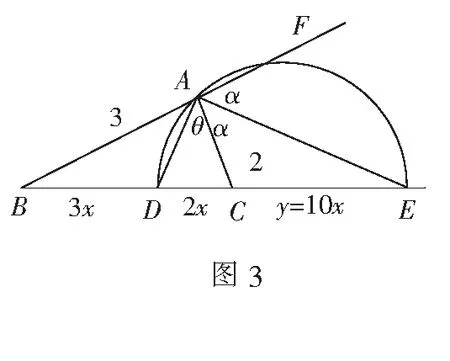
∵AD为∠BAC的角平分线，AE为∠CAF的角平分线，∴∠θ+∠α=90°，即点A的轨迹是以DE为直径的圆.

点评知识具有连贯性，此题便运用了初中数学知识，外角平分线定理、共圆几何条件、极限思维等，利用边界最值求出所需未知量的范围.

解法6(应用三角形性质)

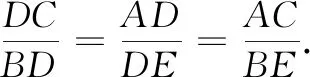
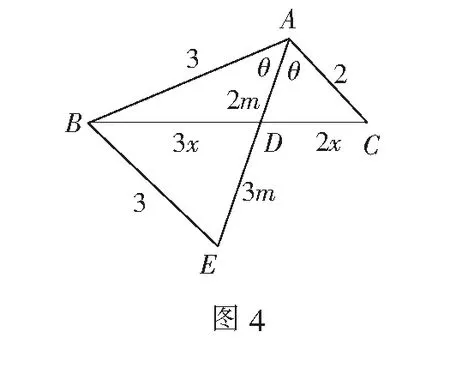
点评学生在平时学习中，容易受“惯性思维”影响，总是会把一些问题复杂化，却忽略了更加简易的方法.构成三角形的条件，对于解决某些含隐含条件的范围问题有奇效.

解法7(相似法)

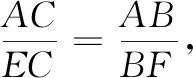
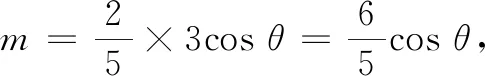
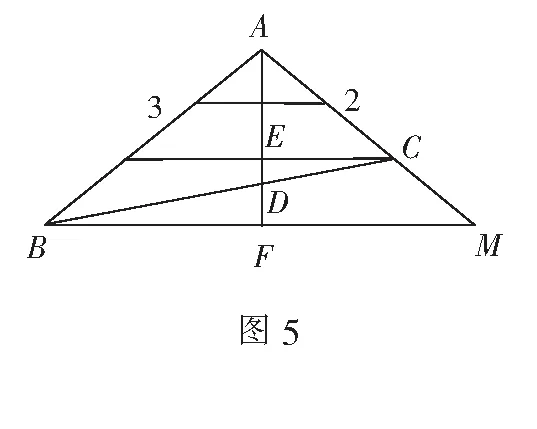
点评相似三角形法是初中几何中常见方法之一，它主要描述了相似三角形边、角的关系.本解法根据几何割补、三角形相似的条件，把原图形补充为等腰三角形，利用相似比最终转化为角度来限定未知量的范围.

解法8(坐标法，函数法)

如图6，设C(2x1,-2y1),x1∈(0,1),B(-3x1,-3y1),y1∈(0,1),BC直线方程为y=kx+b,D(0,b).∵B在BC直线上，

∴-3y1=-3kx1+b.

①

又∵C在BC直线上，

∴-2y1=2kx1+b.

②

点评函数思想是基本的数学思想之一.用函数观点来探求变量的取值范围是通法.

以上八种方法，归根到底都是数形结合思想方法的运用.用几何的观点研究代数问题，可以加强学生数形结合思想的培养，使学生在数和形的联系上把握好一个尺度，能够由数想到形的意义，由形想到数的结构，从而达到快速解决问题的目的.

二、一题多变，让问题由线构成面

把习题通过条件变换、形式变换、因果变换等，使之变为更多的、有价值、有新意的新问题，使更多的知识得到应用，从而获得“一题多练”、“一题多得”的效果.

变式3在∆ABC中，∠A∶∠B=1∶2，∠C的平分线CD把∆面积分为3∶2两部分，求cosA的值.

变式4在∆ABC中，AB=2AC，AD是∠A的平分线，AD=mAC,①求m的取值范围；②若∆ABC的面积是1，求BC最短时m的值.

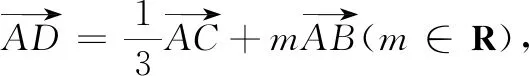
知识是静态的，思维是活动的.在平时的教学中，通过一题多变的训练，能使学生克服思维定势的影响，不局限于某一方面的思考，多角度多方位分析问题、解决问题.既有利于培养学生创造思维，又有利于培养他们的发散思维，达到提高解决综合能力的目的.