精心设置留白 课堂峰回路转——以一道含参恒成立压轴题的讲评为例

万姝玮 蒋 亦

(江苏省奔牛高级中学，213131)

留白是艺术作品创作中常用的一种手法,指书画艺术创作中为使整个作品画面、章法更为协调精美而有意留下相应的空白,留有想象的空间.在数学课堂上,特别是解题教学,教师为了传授给学生更多的方法技能,课堂容量过大,学生难以接受消化.“留白”往往会峰回路转,激活课堂,提高效率,提升体验,堪称艺术!这里以一道高二数学测试题的讲课教学实践为例探究如下.

师:本题难点是参数多,哪个参数最容易处理?

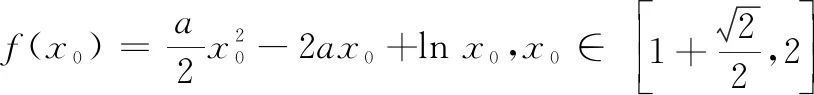
师(板书):-2a+ln 2+ln(a+1)>m(a2-1)-(a+1)+2ln 2对任意a∈(1,2)恒成立.即m(a2-1)-ln(a+1)+a+ln 2-1<0对任意a∈(1,2)恒成立.

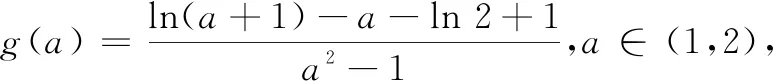
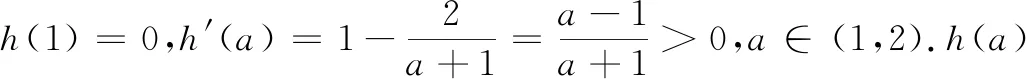
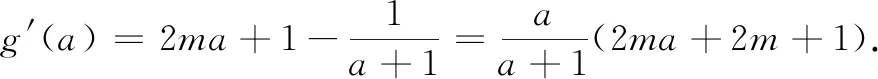
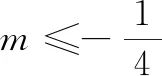
(3)当m≥0时,g′(a)>0,所以,g(a)在(1,2)单调递增，所以g(a)>g(1)=0.

众生:眉头紧皱,个别同学交头接耳,明显有困惑之处.

师:既然大家有困惑,同学们可以自由交流,不明白之处也可以提问.(课堂留白)

5分钟热烈讨论之后,首先回答了学生各种困惑,另有同学提出了多种想法:

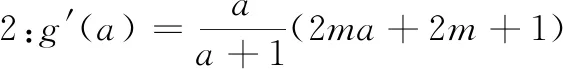
(1)当m≥0时,g′(a)>0,所以g(a)在(1,2)上单调递增，故g(a)>g(1)=0.

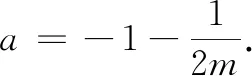
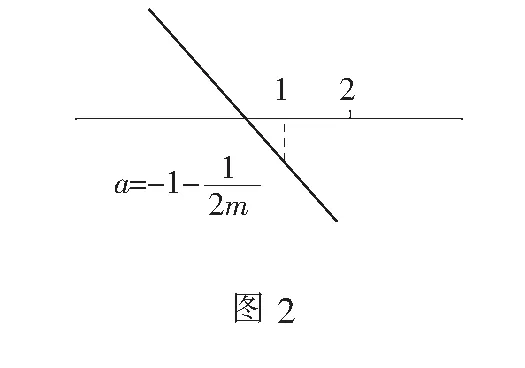
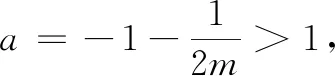
师点评:用导数列表求最值的方法.

第1步，求导函数的零点;

第2步，若零点不存在,则原函数单调(用单调性求最值);若零点存在,则列表求最值.

这位同学“用导数列表求最值”解决含参函数最值问题,比老师的“特值法”找分点更容易理解,也深化了课本中“用导数列表求最值”的方法.

生3:可以将两位同学的方法结合.

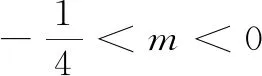
(3)当m≥0时,g′(a)>0,所以,g(a)在(1,2)单调递增，故g(a)>g(1)=0.

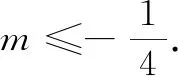
师:这位同学将考察“导函数的零点”改为讨论“导函数是否恒正或恒负”.第1类，当导函数恒正或恒负时,原函数单调;第2类，当导函数不恒正或恒负时,有零点存在,则列表求最值.

当导函数零点难求,值域更容易考察时,这位同学处理方法的优越性就显现出来了,让我们对课本“用导数列表求最值”的方法有了更深刻的认识.老师的“特值法”明确分类标准也有优点,比如当导函数的零点和值域都难求时，解题过程可能更简洁.

可以说,这道压轴题讲评的精彩之处几乎都是学生自主生成的,教师最智慧之处是课堂留白5分钟.当然,课堂留白不是“放羊”,恰当的时机一般是在学生深陷困惑、深受启发之际.正如《学记》所云:“君子之教,喻也道而弗牵,强而弗抑,开而弗达.”