从“数学阅读”试题看核心素养的考查
骆翔燕 周仕荣
(福建省闽南师范大学数学与统计学院,363000)
一、“数学阅读”试题分析
本文选取2019年高考数学理科全国卷中一些“数学阅读”试题,从其分布情况、试题类型及其分析两个方面来探讨所考查的核心素养.
1.试题分布及编号
从表1可知,2019年高考试题中“数学阅读”试题题型多样化,相当注重对于“数学阅读”试题的考查,因而“数学阅读”试题成为检测学生高中阶段学习结果、思维品质与关键能力的主力军,则其对核心素养的表现水平可通过学生对于“数学阅读”试题的解决情况得到体现.
表1 “数学阅读”典型试题在2019年高考试题中的分布情况
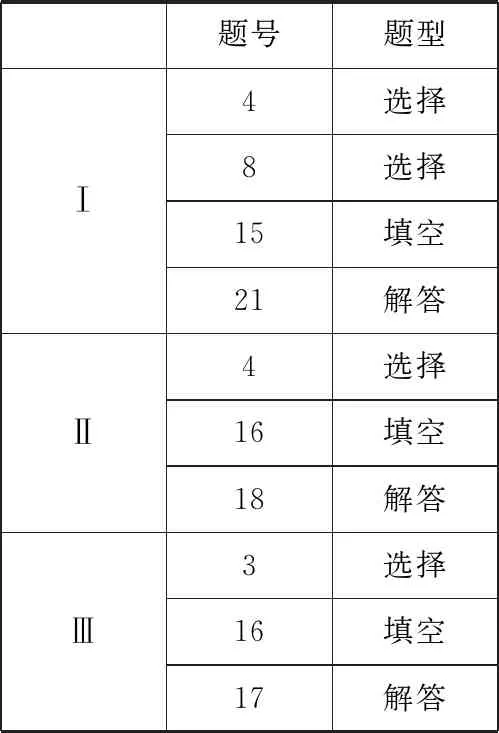
题号题型 Ⅰ4选择8选择 15填空 21解答 Ⅱ4选择16填空 18解答 Ⅲ3选择 16填空 17解答
以下为了方便将试题编号为(卷,题号)的方式来表示试题,如(Ⅰ,4)表示全国卷Ⅰ第4题.以此类推,(Ⅱ,12)表示全国卷Ⅱ第12题.
2.试题类型及其分析
“数学阅读”试题包括阅读材料和问题两部分,其呈现方式多样,按阅读材料的呈现方式不同,可将上述试题划分为“文化型”、“图表型”、“数量型”、“综合型”和“应用型”.
(1)“文化型”试题
“文化型”试题是指以数学文化为参考点形成阅读材料的试题.题(Ⅰ,4)以断臂维纳斯为阅读背景,题(Ⅱ,16)以中国金石文化为阅读背景,因此将题(Ⅰ,4)、(Ⅱ,16)归为这一类.
题(Ⅰ,4)考查黄金分割问题,读题时学生需要对其进行分析、加工,建立起黄金分割模型,并将其表征为接近于个人认知结构的符号语言,达到 “思维中的具体”,以此激活学生对于该知识的认知结构.由阅读材料已给出某人腿长及头顶至脖子下端的长度,这就需要学生利用已有的知识经验去理解“什么叫头顶至脖子下端的长度”以及它与头顶至咽喉的长度有何关系;“什么叫腿长”以及它与肚脐至足底的长度有何关系.推断出其间满足的关系,将其用符号语言表达出来,综合分析,构建出相应的模型,从而使问题得到解决.
题(Ⅱ,16)考查立体几何中棱长的计算问题.题目先介绍了中国的金石文化,旨在让学生领略到数学的对称美,而这一内容的引入实际对于解题毫无帮助,无形之中增加了学生的阅读量.因此,在阅读过程中学生需要能去掉材料中的冗余信息,正确地提取信息并能对其进行有意义的建构.而在信息的刺激下,相关的认知结构就会被激活.阅读包括三个方面:一是识图,即通过阅读图形能将半多面体正确地看成中间层是一个正八棱柱,上下底面各有9个面;二是想图,即通过阅读图形以及所给的图形的文字信息,能够同时处理两类信息,建构起还原后的正方体的思维表象;三是作图,即正确作出还原后的正方体的图形.由图形及相关文字信息抽象出半多面体棱长与正方体棱长的关系,从而解决问题.
(2)“图表型”试题
“图表型”试题是指以图表的形式呈现阅读材料的试题.题(Ⅰ,8)以程序框图的形式呈现试题,题(Ⅲ,17)以统计分析图的形式展现试题,因此将题(Ⅰ,8)题和(Ⅲ,17)归为这一类.
题(Ⅰ,8)的问题表征是图形语言,关于程序框图中的算法问题.在阅读过程中,学生阅读需要关注三个方面:一是找出循环变量的初始条件和终止条件,明晰运算的条件;二是推敲出其运算过程是反复进行相同的操作;三是读懂循环体,掌握运算的方法.依据条件逐步进行推理、分析,从而完成对问题的解决.这一问题解决过程是对学生的数学运算、逻辑推理核心素养的考查.
题(Ⅲ,17)考查频率分布直方图的性质以及频率、平均值的求法.学生需要仔细研读频率分布直方图,获取数据,厘清数据间的关系,紧扣“频率分布直方图的性质”这一突破点,利用分析法将其转化成符号语言,从而计算出a,b的值.第二小问则直接利用平均值的计算公式解决问题.
(3)“数量型”试题
“数量型”试题是指以大量文字的形式呈现阅读材料的试题.题(Ⅰ,21)正是由大量文字语言所表征的,因此将题(Ⅰ,21)归为这一类.
题(Ⅰ,21)考查离散型随机变量分布列、等比数列的证明、数据分析处理问题.学生在阅读题目时,首先给予学生强烈的文字视觉冲击,学生需要对现有材料进行组织、整合,对信息进行有意义构建.学生在阅读的过程中,分析、归纳出X的取值范围,辨析出X的取值与概率间的关系,将其转化成符号语言,并用表格的形式写出分布列,从而解决第一问.通过阅读第一问所求出的分布列以及第二问所呈现的符号语言,厘清其间的关系,利用待定系数法计算出a,b,c的值,并根据递推公式pi=api-1+bpi+cpi+1,对其进行合理的变形,解决第二问的第i问,蕴含了对学生递推思想的考查;第ii问是在阅读第ⅰ问的已证明过的结论这一信息的基础上计算出p4的概率值,对该数值进行分析和推断,以此解释这种试验方案的合理性,体现结论的价值和意义.
(4)“综合型”试题
“综合型”试题是指以其他学科内容为背景形成阅读材料的试题.题(Ⅱ,4)以物理学科的内容为阅读背景,题(Ⅲ,3) 以文学作品四大名著为阅读背景,因此将题(Ⅱ,4)、(Ⅲ,3)归为这一类.
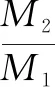
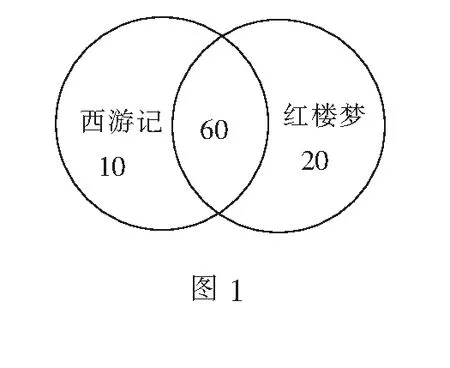
题(Ⅲ,3)考查估计值的求解问题.学生在阅读题目时,学生要能够识别问题类型,找出信息间的相互联系,以此激活学生的认知结构.而文字语言给人以视觉冲击,眼花缭乱,容易导致学生思绪混乱.因而可借助于集合论中韦恩图(如图1)这一图形语言来帮助理解,明晰思路,其中蕴含着集合思想的考查.利用图象语言可推断出只阅读过《西游记》的人数为10人,从而推断出阅读过《西游记》总的人数为70人,继而解决问题.
(5)“应用型”试题
“应用型”试题是指以生活实际应用为背景形成阅读材料的试题.题(Ⅰ,15)、(Ⅱ,18)分别引入篮球、乒乓球比赛这些实际生活中的应用为阅读背景,题(Ⅲ,16)以学生到工厂参加劳动实践为阅读背景,因此将题(Ⅰ,15)、(Ⅱ,18)、(Ⅲ,16)归为这一类.
题(Ⅰ,15)、(Ⅱ,18)考查了两个随机事件独立的含义,且会利用相互独立事件概率乘法公式来计算概率,是新课标中概率所要求掌握的内容.在阅读过程中,学生需要能够捋清所求事件可能出现的全部情况,以做到不重不漏,这一过程体现出数学思维的严谨性,意在对学生分类思想的考查.依据现实生活经验明白每场比赛出现的结果是相互独立的,学生就会搜索出在自己的知识空间中与之相关联的运算法则,从而解决问题.
题(Ⅲ,16)考查几何体体积的计算.在阅读过程中,学生可以清晰地知道本题是要求制作模型所需原料的质量,而题目中原料密度已给出,因此只需求出模型的体积便可解决问题.对于该模型体积的求解可转化成“长方体体积与四棱锥体积之差”,而对于四棱锥体积的计算,由图形语言学生需读懂四棱锥的高为长方体长的一半,由文字语言学生应依据自身的陈述性知识读出“四棱锥的底面为菱形”,从而利用菱形计算公式求出底面积,其中蕴含了化归与转化思想、综合法等等.
二、考查特点及建议
通过对2019年“数学阅读”试题解决的过程分析,可以看出每道试题考查的素养并不单一,凸显了素养考查多元化,也反映出“数学阅读”试题成为素养考查的重要的载体. 同时,我们还可以看到“数学阅读”试题涉及立体几何、概率统计等方面,涉及面广,从侧面反映了其素材丰富.由此提出几点建议:
1.重视数学教材的阅读
数学教材是学生学习数学的第一手媒介,学生的数学阅读也应始于此.一方面,数学教材是由专家充分考虑学生的认知规律、学生的生理、心理特点、数学学科特点而编制的,因而学生的语言表达、符号的使用有了参照模板,通过阅读教材,可以使其规范化.另一方面,人教版教材“阅读与思考”一栏呈现的是数学家、数学发展史、著名的数学问题、显示生活等方面的介绍,可以看到这些阅读材料来源广泛,涉及方方面面,学生阅读数学教材的过程即是前人思维清晰再现的过程,在阅读过程中体会前人是站在何种高度去解决瓶颈问题的.
2.重视数学阅读的知识教学
“四基”的落实有助于数学核心素养的形成,而基础知识是其他三基的基础,故而知识教学是最为基础的教学活动.这里的知识教学主要是指针对数学概念、定理和法则,甚至一些具体的数学思想方法等,以及由此构成的数学知识系统的认识和理解的教学[2].教师对于知识的教学应充分尊重学生的认知结构,还原知识发生发展的全过程,提供直观实例丰富学生的表象系统,从感性到理性,从具体到抽象.
3.重视数学阅读的解题教学
在解题教学中,应注意暴露自身的阅读思索过程,让学生捕捉教师是如何抓住题目关键信息点,如何对其进行合理的表征,选择恰当的算理以及如何从数学思想方法的视角去解决问题的,从而让学生在数学阅读题中无所畏惧,抓关键点迅速解决问题.

