构建知识网络 明晰解题方法——以“立体几何中的平行关系”为例

苏汉杰

(首都师范大学附属中学(通州校区)，101100)

立体几何是研究空间图形及其关系的一门学科,是高中数学中重要而又独立的一部分,学习立体几何能够培养学生的空间想象能力和逻辑思维能力.除了要熟练掌握公理、定义和定理之外,还应该将这些公理、定义和定理的关系梳理清楚,构建知识网络,这样才能对立体几何的认知更加深入,才能够熟练利用所学知识解决相关问题.

一、知识网络

立体几何中的平行关系包括“线线平行”、“线面平行”和“面面平行”,有6个定理将这些平行关系联系了起来,构成了平行关系的知识网络,如图1.

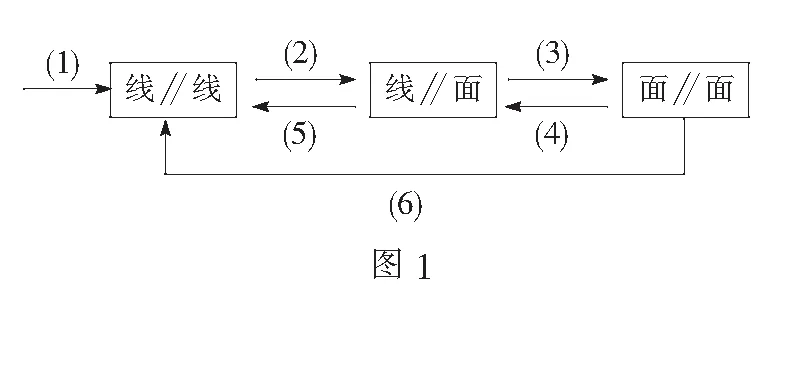
(1)公理4:平行于同一条直线的两条直线平行;

(2)线面平行判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;

(3)面面平行判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行;

(4)平行定义:如果两个平面平行,那么在一个平面内的直线必平行于另一个平面;

(5)线面平行性质定理:如果一条直线与一个平面平行,那么过这条直线的任一平面与此平面的交线与该直线平行;

(6)面面平行性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.

通过几个例题来具体看看如何应用这些定理解决立体几何中的平行关系.

二、应用举例

例1如图2,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,点D，E分别是BC和A1C1的中点,求证:DE∥平面ABB1A1.

思路1取A1B1的中点F(或取AB的中点G),根据线面平行判定定理进行证明,即线∥线→线∥面.用直尺将直线DE往平面ABB1A1中平移,如果沿着直线DB平移,当点D移到点B的位置时,这时直尺停留在与直线A1B1相交的位置F(图3),这样就可以大胆猜测点F就是直线A1B1的中点,经过这样的操作确认和直观感知后,就可以通过证明四边形BDEF是平行四边形进行验证了.当然也可以沿着直线A1C1进行平移.

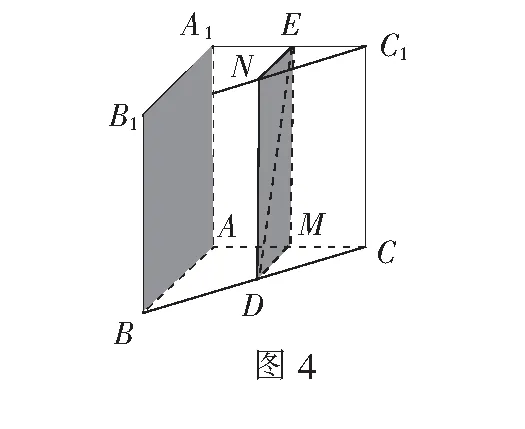
思路2取B1C1的中点(或取AC的中点),根据平行定义,先构造面面平行,然后再证明线面平行,即面∥面→线∥面.如何构造过直线DE与平面ABB1A1平行的平面呢?首先,过直线DE有且仅有一个平面与平面ABB1A1平行.根据面面平行判定定理,除了直线DE之外,还应该再找到一条直线与平面ABB1A1平行,同时,这条直线应该与直线DE相交,这样就可以找到过直线DE与平面ABB1A1平行的平面了(如图4).

例2如图5,在四棱锥P-ABCD中,AB∥DC,DC>AB,在线段PD上是否存在点F,使得直线AF∥平面PBC,并说明理由.

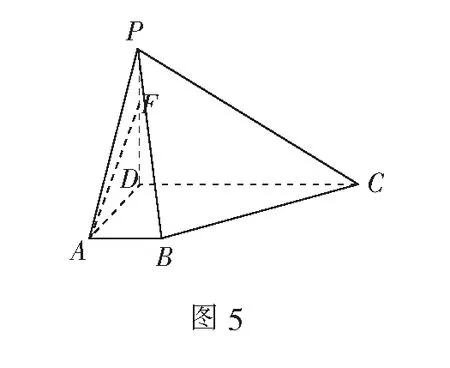
解析本题如果利用线面平行的判定定理来解决,对学生的思维量要求较高,不太容易操作.仿例1思路2,可以通过构造面面平行来解决.首先过直线AF构造与平面PBC平行的平面,这个平面需要过A的另外一条直线确定,故先过A构造与直线BC平行的线,这样的线肯定与平面PBC平行,然后再构造EF与直线PC平行,这样平面AEF与平面PBC平行,点F的位置就确定了(图6).

变式如图7,在四棱锥P-ABCD中,AB∥DC,DC=2AB,在线段PD上是否存在点G,使得直线PB与平面AGC平行?并说明理由.

解析假设存在点G,使得直线PB与平面AGC平行,那么,由线面平行性质定理可知,过直线PB的平面与平面AGC的交线与直线PB平行,这样就可以确定点G的位置了.同时,再由线面平行判定定理可知,此时的点G满足OG平行PB,自然就能保证PB与平面AGC平行了.

立体几何中的平行关系中虽然“线面平行”是纽带,但是“线线平行”是核心.只有紧紧抓住这个核心,利用平移的操作方法先大致确定要求的“线”的位置,然后根据平面几何或者公理4进行证明,其他的问题其实都可以以“线线平行”为基础,根据平行的相关公理进行推导.

几何学是研究现实世界中物体的形状、大小与位置关系的数学学科,所以在立体几何学习过程中,通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质.教材中的公理、定理和定义是我们研究空间图形关系的基础和依据,相互之间是联系的,是一个知识网络,是一个有机整体.立体几何的学习要遵循立体几何的特点,不能忽视了直观感知、操作确认,而把立体几何的学习当成纯碎的应用一条条定理进行思辨论证和度量计算的训练.