探究多边形的外角和

李榃

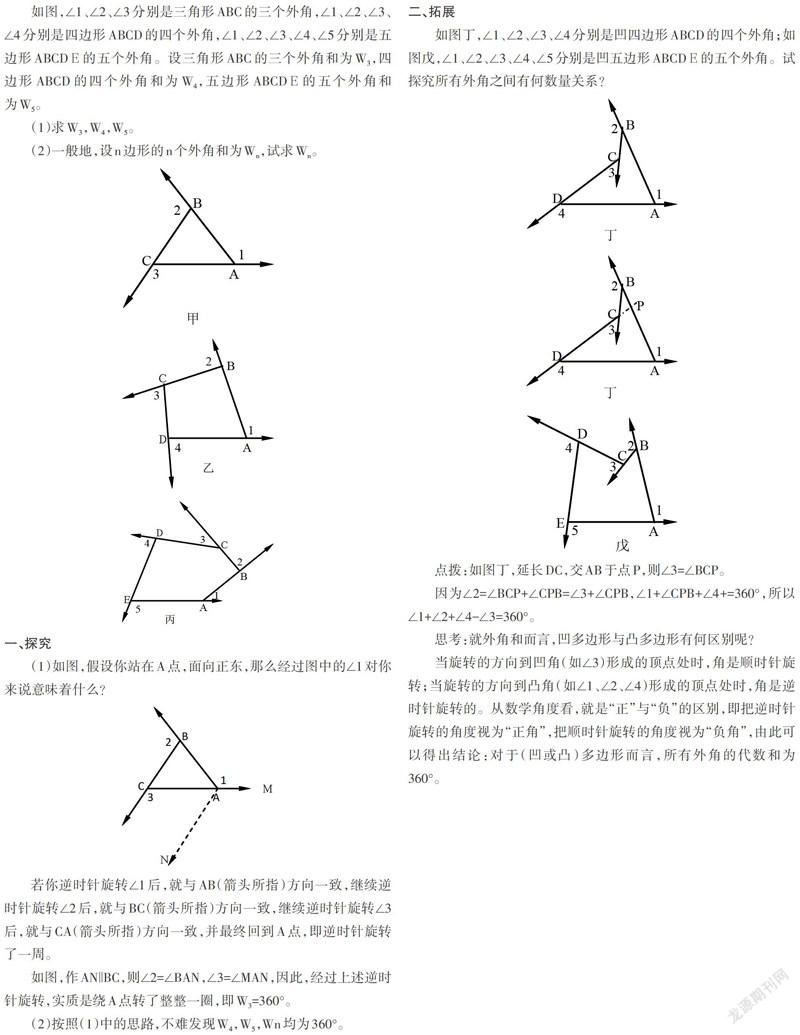
如图，∠1、∠2、∠3分别是三角形ABC的三个外角，∠1、∠2、∠3、∠4分别是四边形ABCD的四个外角，∠1、∠2、∠3、∠4、∠5分别是五边形ABCDE的五个外角。设三角形ABC的三个外角和为W3，四边形ABCD的四个外角和为W4，五边形ABCDE的五个外角和为W5。

（1）求W3，W4，W5。

（2）一般地，设n边形的n个外角和为Wn，试求Wn。

一、探究

（1）如图，假设你站在A点，面向正东，那么经过图中的∠1对你来说意味着什么？

若你逆时针旋转∠1后，就与AB（箭头所指）方向一致，继续逆时针旋转∠2后，就与BC（箭头所指）方向一致，继续逆时针旋转∠3后，就与CA（箭头所指）方向一致，并最终回到A点，即逆时针旋转了一周。

如图，作AN∥BC，则∠2=∠BAN，∠3=∠MAN，因此，经过上述逆时针旋转，实质是绕A点转了整整一圈，即W3=360°。

（2）按照（1）中的思路，不难发现W4，W5，Wn均为360°。

二、拓展

如图丁，∠1、∠2、∠3、∠4分别是凹四边形ABCD的四个外角;如图戊，∠1、∠2、∠3、∠4、∠5分别是凹五边形ABCDE的五个外角。试探究所有外角之间有何数量关系？

点拨：如图丁，延長DC，交AB于点P，则∠3=∠BCP。

因为∠2=∠BCP+∠CPB=∠3+∠CPB，∠1+∠CPB+∠4+=360°，所以∠1+∠2+∠4-∠3=360°。

思考：就外角和而言，凹多边形与凸多边形有何区别呢？

当旋转的方向到凹角（如∠3）形成的顶点处时，角是顺时针旋转;当旋转的方向到凸角（如∠1、∠2、∠4）形成的顶点处时，角是逆时针旋转的。从数学角度看，就是“正”与“负”的区别，即把逆时针旋转的角度视为“正角”，把顺时针旋转的角度视为“负角”，由此可以得出结论：对于（凹或凸）多边形而言，所有外角的代数和为360°。