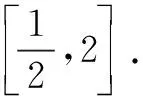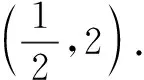错题资源与微专题教学——以导数在研究函数单调性上的应用为例

相 建

(江苏省宝应县氾水高级中学，225819)

在教学实践中，经常有一部分学生对于相同的错误屡犯不止,学习效率大打折扣．为了利用错题这一资源为教学服务,教师可以收集错题整合成微专题,通过归纳、总结，以达到提高学生对知识的有效把握的目的.

利用导数判断函数的单调性，是高考必考内容之一,是高考考查的重点,其主要题型以函数单调区间的求解,单调性的证明,已知函数的单调区间求参变量的取值范围为主．而熟练掌握导数与函数单调性的关系是解题的突破口．本文以此为专题整合错题资源，供教学参考.

题型1利用导数证明函数的单调性

例1(1)证明:函数f(x)=-2lnx+x2在(1,+∞)上是增函数;

(2)证明:函数f(x)=x-sinx在R上是单调增函数.

分析此题是利用导数证明单调性的问题,直接利用导数的符号与函数单调性的关系证明即可．其基本解题步骤为:① 求函数的导数并将其写成可以判断符号的形式(往往可以化成两个基础函数的积或商的形式，如本题的第(1)问,但本题的第(2)问有点特殊);② 判别导函数在给定区间上的符号;③ 下结论(即若有导函数f′(x)>0在区间D上成立，则原函数f(x)在区间D上单调增;若有导函数f′(x)<0在区间D上成立,则原函数f(x)在区间D上单调减).

证明(1)∵f(x)=-2lnx+x2，

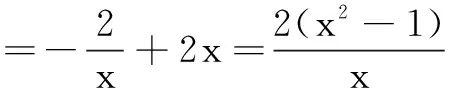
∵x>1，(x+1)(x-1)>0,

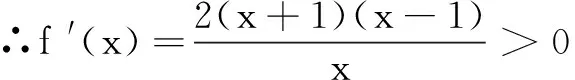
(2)∵f(x)=x-sinx,∴f′(x)=1-cosx.∵x∈R,∴cosx∈[-1,1],∴-cosx∈[-1,1],∴1-cosx∈[0,2],即1-cosx≥0在R上恒成立.∴函数f(x)=x-sinx在R上是单调增函数.

题型2利用导数求函数的单调区间

例2求函数f(x)=x3-15x2-33x+6的单调减区间.

分析用导数研究函数的单调性是非常简便的,它可以避免用定义确定函数单调性所带来的繁琐运算.求函数的单调区间的基本步骤为:① 确定函数f(x)的定义域；② 求导数f′(x);③ 由f′(x)>0(或<0)求出相应的x的取值范围．解不等式f′(x)>0,可得单调递增区间,解不等式f′(x)<0得单调递减区间.

解由f(x)=x3-15x2-33x+6得定义域为R,且f′(x)=3x2-30x-33=3(x+1)(x-11).令f′(x)<0得-1

点评使f′(x)<0的取值区间如为一个,则此区间为其单调区间,如为两个或两个以上,在各自区间上均为单调函数,在这里不能将这两个区间并起来．如此函数单调递增区间写成 (-∞,-1)∪(11,+∞)就错了,应写出单调递增区间为(-∞,-1),(11,+∞).

题型3已知函数的单调区间,求参变量的范围

例3(1)已知函数f(x)=mx2+lnx-2x在定义域内为增函数,求实数m的取值范围；

(3)若函数f(x)=x3+ax有三个单调区间,求实数a的取值范围.

分析第(1)问的处理方法是将函数的单调性问题转换为f′(x)≥0在定义域内恒成立.

第(3)问求a的取值范围的处理方法是由f(x)=x3+ax有两个极值点.

(3)由函数f(x)=x3+ax有三个单调区间可得f(x)有两个极值点,即f′(x)=0有两个不等的实根,即3x2+a=0的两个不等的实根,易得a<0.

题型4构造函数,利用单调性解题

例4已知定义域为R的函数f(x)满足f(1)=3,且f(x)的导数f′(x)<2x+1,则不等式f(2x)<4x2+2x+1的解集为______.

这个题目需要构造新的函数并利用单调性进行求解．根据题目的特点,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧．许多问题,如果运用这种思想去解决,往往能获得简洁明快的思路,有着非凡的功效.

首先，在数学课堂教学中，应该给学生提供更多的思考与合作交流的机会,创造有利于学生思考的宽松的课堂氛围,让学生尝试自己去编制个性化的微专题,鼓励学生大胆地质疑,尽可能引导学生参与教学过程,尽可能把学习的主动权交给学生,使教师真正成为课堂活动的组织者.

其次,我们要注意整合错题资源．教学的成功并不取决于微专题题数量的多少,而在于整合的错题资源以及进行的微专题是否具有典型性、必要性和合理性．我们提倡开展微专题复习,并不是说所有的教学内容都要求进行微专题．要克服单纯地为了微专题而微专题,给学生造成过重的学习和心理负担,让学生产生逆反心理,反而事倍功半.

另外,整合错题资源、微专题教学的起点一般源于课本上的例、习题．在设计微专题时，要做到源于教材又高于教材,不脱离教材,不脱离学生的实际．否则将会加重学生的学习负担,产生厌学情绪,不利于复习效果的提高.

实践证明,在高三的数学复习教学中，适时采用微专题教学法,可以帮助学生更好地构建知识结构,熟悉每一种题型的通性通法,通过学一道题达到会解一类题的效果.有利于学习效率的提升和减轻学生的学习负担，有利于培养学生学习数学的兴趣,从而使数学课堂更加高效.