一题一课 跳出题海*——以2019年高考数学全国Ⅰ卷文科第12题为例

李 超 孔德宏

(云南师范大学数学学院，650500)

波利亚指出:“拿一个有意义又不复杂的题目去帮助学生发掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域”.解题教学亦是如此，要充分发挥例题的作用.笔者以一道高考试题的教学为例，阐述自己的一些思考.

一、试题呈现

(2019年全国高考数学Ⅰ卷文科第12题)已知椭圆C的焦点为F1(-1,0),F2(1,0)，过F2的直线与C交于A，B两点.若|AF2|=2|F2B|,|AB|=|BF1|，则C的方程为( )

二、一题多想

解题教学不仅要教学生获得解题活动的结果，而且要暴露学生在解题过程中的思维活动.教师引导学生抓住题目的关键点:由题目已知c的值,根据方程思想，只需要再找到a,b，c的一组关系，就可以求出椭圆的方程.利用方程思想找关系时，学生就会产生诸多想法.

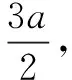
想法2利用三角形相似求出点B的坐标，再把点B的坐标代回椭圆方程，从而构造出关于a的一个方程.

想法3注意到|AB|，|BF2|,|AF1|都可以用a来表示，并且∆AF1F2和∆AF1B有公共角∠F1AF2，可联想到余弦定理，得到关于a的一个方程.

想法4∠BF1A余弦值可以求解，可联想到平面向量基本定理，两边平方便转化为关于a的一个方程.

想法5涉及到过焦点的问题，可以考虑用焦半径公式解决.

想法6运用直线的参数方程是处理定比点分问题的常用的方法，可以利用t的几何意义和比值关系构造出关于a的一个方程.

三、一题多解

从学生不同的想法出发，理清解题思路，对解题的可行性进行分析，研究解题方法，培养学生的发散思维.

解法1利用弦长公式求解.

由于|AB|=|BF1|,|AF2|=2|F2B|,所以2a=|BF2|+|BF1|=|BF2|+|AB|=|BF2|+|AF2|+|BF2|=2|AF2|.故|AF2|=a,因此点A为椭圆上顶点或下顶点.根据椭圆的对称性，我们考虑点A为上顶点的情况，如图1.

解法2利用相似三角形求出点B的坐标，再代入椭圆方程求解.

过点B作x轴的垂线交于点B1,如图2.

解法3运用两次余弦定理求解.

(注：由cos∠AF2F1=-cos∠F1F2B也可以求出a)

解法4余弦定理+平面向量基本定理.

解法5利用椭圆焦半径公式求解

解法6运用直线的参数方程求解

由于直线AB的参数方程为：

四、一题多思

在教学中有学生提出了下面两种解法.

上面这两种解法在思路上并没有错，但为什么解不出结果呢？方程反映了同一事物在2种不同的表现形式下有相等关系，也反映了2种事物在不同形式上有相等关系[1].上述解法实质上是同一事物在同种表现形式下的相等关系，即自身和自身相等，无法解出结果.因此，建立方程时，教师需向学生强调要找表现形式不同的相等关系.

五、一题多变

对于同一类问题，可以从不同的角度进行不同形式的变式通过变式，让学生对此类问题有一个系统的认识，做到会一题通一类.

解题教学中，教师要以学生为中心，充分暴露出学生在解题过程中的思维活动，让学生的思维在解题中得到有效地锻炼，题目千千万万，刷百题而不如解透一题！