运用同构式培养运算能力
2020-09-05 00:41:46张晓华
高中数学教与学 2020年14期
张晓华
(广东省深圳市人大附中深圳学校,518119)
“同构式”是指结构相同或类似的两个式子,在高中数学各大板块中都能看到,既可以代数同构,也可以几何同构;既可以类比同构,也可以递归同构.运用“同构式”进行运算设计、解决问题,是培养运算能力、逻辑推理和抽象概括能力的有效途径.在解题过程中我们如果善于用好同构式,学会观察分析、概括抽象、欣赏反思,对改善运算能力会有较大作用.
一、运用同构式构建新函数
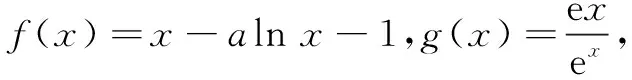
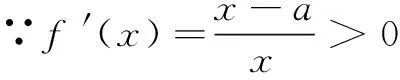
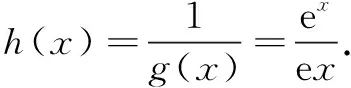

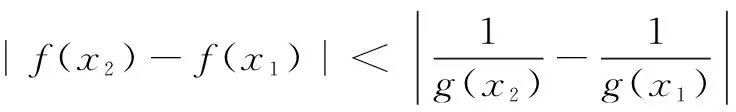

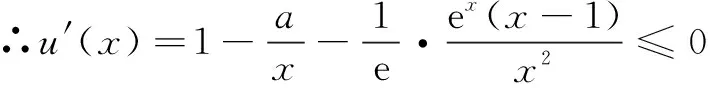
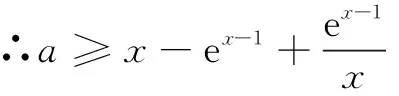



本例通过设定x2>x1后去绝对值,移项得f(x2)-h(x2) an+2-san+1=t(an+1-san), 即an+2=(s+t)an+1-stan. ① ② 由① ② 消去an+1,得 解设直线l:y=k(x-2),可得R(0,-2k).设A(x1,y1),B(x2,y2), ① 因为A在椭圆上, 同理可得μ2+10μ+5-20k2=0. ∴λ,μ为方程x2+10x+5-20k2=0的两个不同根, ∴λ+μ=-10为定值. 在《普通高中数学课程标准(2017 年版)》中,核心素养“数学运算”这样定义:“数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的过程.主要包括: 理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等.数学运算是解决数学问题的基本手段;数学运算是一种演绎推理,是计算机解决问题的基础.”这也说明,数学运算能力绝不是单一能力,也需要逻辑分析、抽象概括、探究发现来支撑.抓住同构式的特点,体验同构式优美的对称形态,感受同构式背后所蕴含的核心意义,是自觉使用的关键.二、运用同构式构建递推关系
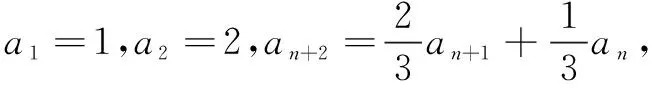




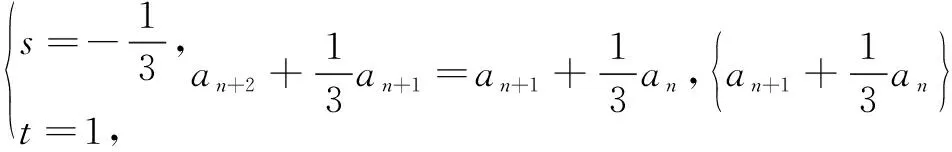
三、运用同构式构建方程组
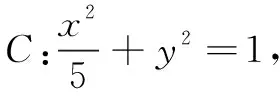

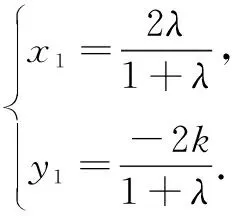
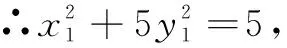

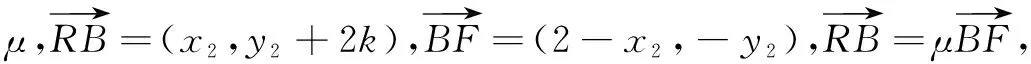
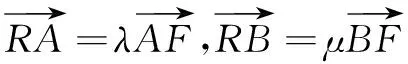
猜你喜欢
中学生数理化(高中版.高二数学)(2022年6期)2022-06-30 06:36:02
中学生数理化(高中版.高考数学)(2022年1期)2022-04-26 14:09:30
小学生学习指导(中年级)(2022年4期)2022-04-26 06:34:46
今日农业(2021年9期)2021-11-26 07:41:24
中学生数理化·七年级数学人教版(2021年10期)2021-11-22 07:53:00
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19 08:54:16
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19 08:54:02
高师理科学刊(2020年2期)2020-11-26 06:01:30
数学小灵通(1-2年级)(2020年6期)2020-06-24 05:57:54
数学小灵通·3-4年级(2017年10期)2017-11-08 08:42:51

