构造图形巧解平面向量模的取值范围问题*

闫 伟

(广东省中山市濠头中学，528437)

平面向量具有“形”和“数”的双重性,是沟通代数、几何和三角的重要工具.平面向量模是一个实数,是向量的一个核心概念,与平面向量的运算紧密相关,而且具有明确的几何意义.因此，平面向量的模,特别是与模有关的最值或取值范围问题，常常出现在知识点的交汇之处,着眼于向量知识,与矩形、圆、椭圆等几何图形联系紧密,思维跨度大且解法灵活. 本文分类例说借助几何图形巧解向量模的取值范围问题,供大家参考.

一、构造矩形

例1已知|a|=|b|=2,|c|=1,(a-c)(b-c)=0,则|a-b|的取值范围是______.

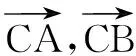
二、构造圆

例2已知a,b是平面内互不相等的两个非零向量,且|a|=1,a-b与b的夹角为150°,则|b|的取值范围是______.

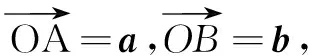
评注将向量转化到∆ABO中,根据|a|=1及其对角∠ABO=30°可以确定点B的轨迹是圆,然后借助圆的直观性质求解,极大地提高了解题效率.

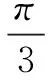
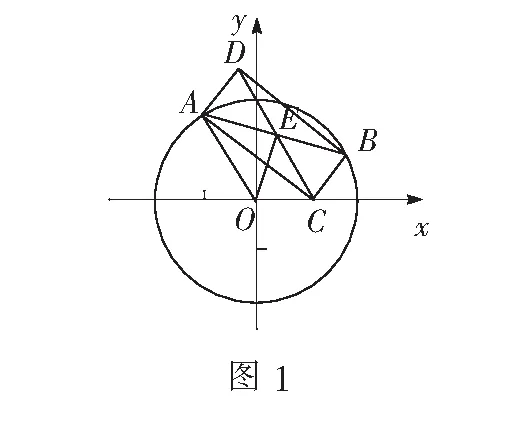
评注本题由向量相等关系巧妙地将c-a+2b转化到同一个三角形中,从而确定点C的轨迹是半径为2的圆,|c|表示圆内定点到圆上的点的距离,借助圆的特性可快速锁定结论,解题中根据向量模的几何意义加强这类转化思想的应用.

三、构造椭圆

例4已知平面向量a,b满足|a|=1,4-a·b=2|a-b|,则|a+b|的取值范围是______.

评注本题的几何意义较隐蔽,难度较大,先借助坐标将条件等式中蕴含的椭圆显现出来,再根据向量模的几何意义确定|a+b|是椭圆焦点与椭圆上点的距离,解题思路清晰,关键是抓住向量模的本质进行转化.

四、构造抛物线

评注由本题条件可知A,B的相对位置是确定的,关键是确定动点C的轨迹.从几何的角度进行转化得到抛物线方程,于是原问题转化为抛物线上的点到定点B(1,1)与到焦点A(1,0)的距离之和的最小值问题.再结合抛物线的定义准确快速地解决问题,本题若直接根据向量模运算求解很难求得结论.利用转化思想将代数问题几何化,体现了数形结合的优越性.

在解题教学过程中,数形结合已作为一种重要的数学思想方法,借助图形,可以使许多数量关系(如文章中的向量模)、抽象的概念直观化、形象化,免去因计算而带来的冗长与枯燥乏味,从而极大地提高解题效率.