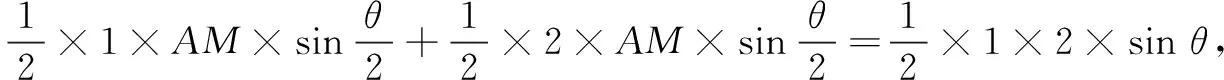探源头 补短板 思本质——例谈一题多法的讲评设计

刘在云

(江苏省仪征市教学研究室 ，211400)

在高三教学视导听课中,常常会听到老师们对部分试题的讲评注重一题多法.有些听起来非常精彩,老师深入剖析,有理有据,让学生能从不同角度去分析问题,感受到了数学学科因方法的灵活、知识的互通而彰显出的魅力,提高了解决问题的能力.但也有些就纯粹是多种方法的罗列,常常置学生较熟悉的常规解法于不顾,偏偏另辟“蹊径”,跟学生讲解一些根本不易想到的奇门怪招,不知不觉中加大了数学学习的难度,增加了学生的畏难情绪,反而降低了教学效果.

笔者认为,经典试题确实是宝贵的教学资源,精彩的讲评更是提高学生解决问题能力的重要途径.一题多法,带领学生探究各种方法的来源(即怎么想到的),呈现求解过程中的注意点、关键点、易错点、迷糊点并及时强化(即具体如何解),解题后再及时反思各种解法本质(即为什么可以这样解),就是一种精彩的讲评.

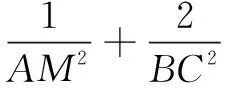
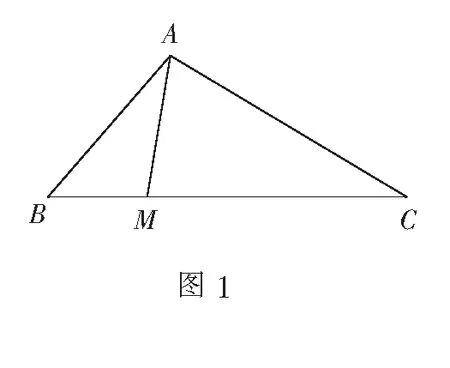
一、分析题意,探究并实施常规解法

本题条件简洁明了,是给定两边长的一个三角形,无法从中推出新的结论或结果,而目标是求一含有两未知量表达式的最小值.联想求最值的常规思路:基本不等式或构造函数．若运用基本不等式,那需要有两变量AM2与BC2之间的等式关系,显然此处不够明显,需要探寻．若回到构造函数的思路上,那便需要统一到一个变量上来!回到图形上,不难判断变量应选择边AM长或是BC边长(为计算方便可选BM长)或∠BAC.当然如何利用图形建立AM与BC边长的等量关系,以及如何用∠BAC来表示AM长，对部分学生来讲是个“短板”,不是那么清晰,需要通过讲评进行强化．可先从更贴近学生思维的函数角度作出如下处理.

方法1设BM=x，则BC=3x,那么AM等于多少呢(用x表示)？可引导学生发现通过以下两个途径列方程求出(笔者从多次听课中发现这是学生不够熟练的一块,可视为短板),就此指导学生如何在关联三角形中构建方程,强化方程的思想.

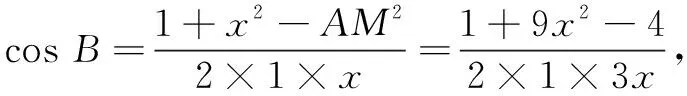
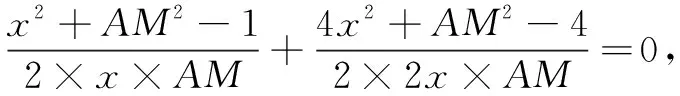
方法2设AM=t,那么BC等于多少呢(用t表示)？相信学生受方法1中思考1与思考2的启发,很快想到如下的思考3与思考4,也达到了及时巩固“在关联三角形中构建方程”这一短板.

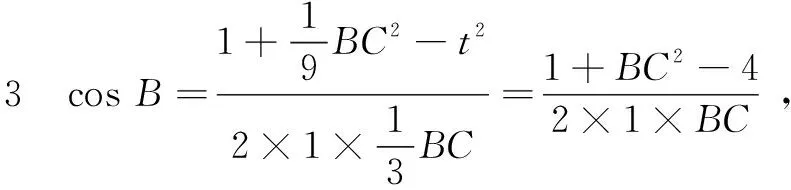
思考4由cos∠AMB+cos∠AMC=0得

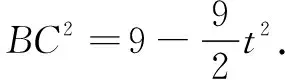
途径1视为函数先求导,再求导根,进而求出最小值.

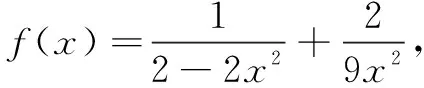
途径2根据目标式的结构,可借助“常数代换”,进而利用基本不等式求其最小值.

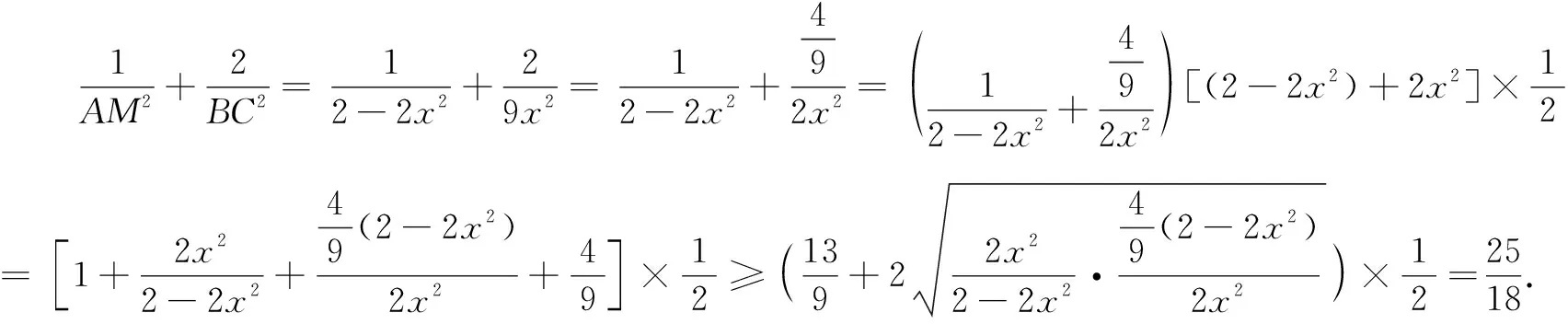
二、提出新问题,培养提升思维品质

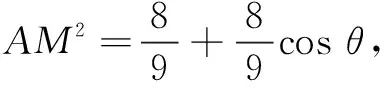
三、另辟新路,增强数形结合能力

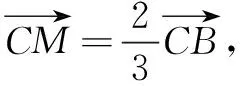
四、变式对比,引领推动反思本质