永远的定义域
李小蛟
(四川省成都树德中学 610000)
函数定义域是指在对应法则下自变量的取值范围,相同法则作用的整体应该一致.所以笔者认为处理复合函数定义域只需要记住“两个永远”:定义域永远指x范围,括号内范围永远不变.
1.已知f(x)的定义域,求f[g(x)]的定义域
例1已知f(x)的定义域为[4,6],求①f(2x+1),②f(|3x+1|)的定义域.
分析本题给出f(x)的定义域为[4,6],即表示f(x)中x的范围为[4,6],此时f(x)括号内只有x,所以在相同法则f作用之下的括号内范围均应该为[4,6].
解①∵f(x)的定义域为[4,6],

②∵f(x)的定义域为[4,6],
∴4≤|3x+1|≤6,
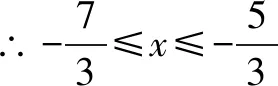

评析已知f(x)的定义域为[m,n],求f[g(x)]的定义域,根据复合函数定义域“两个永远”法则,只需令m≤g(x)≤n,求解出x的范围即为f[g(x)]的定义域
2.已知f[g(x)]的定义域,求f[h(x)]的定义域
例2已知f(3x+1)的定义域为[4,6],求f(2x+1),f(|3x+1|)的定义域.
分析本题给出f(3x+1)的定义域为[4,6],即f(3x+1)中x的范围为[4,6],此时f(3x+1)括号内为3x+1,所以13≤3x+1≤19,因此在相同法则f作用之下的括号内范围均应该为[13,19].
解①∵f(3x+1)的定义域为[4,6],有4≤x≤6,
∴13≤3x+1≤19.根据复合函数定义域可知13≤2x+1≤19,
∴6≤x≤9,即f(2x+1)的定义域为[6,9].
②∵f(3x+1)的定义域为[4,6],
∴13≤3x+1≤19.
根据复合函数定义域可知13≤|3x+1|≤19,
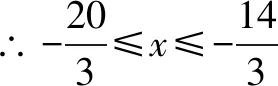
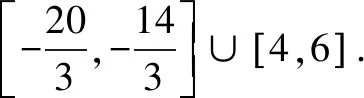
评析已知f[g(x)]的定义域为[m,n],求f[h(x)]的定义域.根据复合函数定义域“两个永远”法则,只需求出g(x)的值域[p,q],再令p≤h(x)≤q,求解出x的范围即为f[h(x)]的定义域.
通过以上例析,我们不难发现,复合函数定义域虽然不易理解,难以掌握,但只要记住两个永远(定义域永远指x范围,括号内范围永远不变),就永远不会出错.

