聚焦柯西不等式在竞赛中四大运用

朱小扣 樊惟媛

(1.安徽省无为第三中学城北校区 238300;2.上海市嘉定区第一中学 201808)

柯西不等式在竞赛中不等式的证明与代数式最值的计算，有着十分重要的作用.与此同时，柯西不等式经常也与其他不等式结合使用，能解决出很多有难度的试题.本文旨在帮助同学们突破有关柯西不等式运用的难点和热点问题.

一、知识点梳理

当且仅当ai=kbi，即ai,bi(i=1,2,3,…,n)成比例时取等号.

二、命题规律揭示

1.柯西不等式的直接运用

例1 (2018年河北初赛题)已知实数x,y,z满足x2+y2+z2=3,x+2y-2z=4,则zmax+zmin=____.

解由柯西不等式得：(x2+y2)(12+22)≥(x+2y)2，故(3-z2)·5≥(4+2z)2

例1是通过移项把z移到一边，从而对x,y用柯西不等式，得到了z的范围.

≤(x2+2-x2)(1-x2+x2)=2.

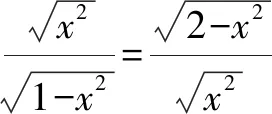
例3 (2018年河南初赛)已知cos(α-β)=cosα+cosβ，试求cosα的最大值.

解由cos(α-β)=cosα+cosβ得：cosβ(cosα-1)+sinβsinα=cosα.

由柯西不等式得：

cos2α=[cosβ(cosα-1)+sinβsinα]2

≤(cos2β+sin2β)[(cosα-1)2+sin2α]

评析由柯西不等式可以直接求出上面这一类题的最值，特别在例2，例3中的应用，应该引起大家的重视.

2.结合待定系数法使用

解由柯西不等式得：

于是，

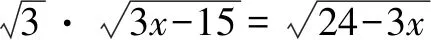
利用待定系数法与柯西不等式也是解决此类问题常用的方法.此法不仅可以求出含两个根号的函数的最大值，只要用法得当，还可以求出含多个根号的函数的最大值.

解由柯西不等式并结合待定系数法可得：

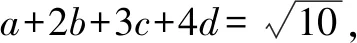
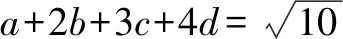
由柯西不等式得：

[(1-t)2+(2-t)2+(3-t)2+(4-t)2+t2][a2+b2+c2+d2+(a+b+c+d)2]

≥[(1-t)a+(2-t)b+(3-t)c+(4-t)d+t(a+b+c+d)]2=10.

于是，

a2+b2+c2+d2+(a+b+c+d)2

评析运用柯西不等式结合待定系数法可以解决很多类似的题.待定系数法配凑系数，是很有技巧性的,待定后配凑可进一步延拓了柯西不等式解题范围.

3.用其他的不等式预处理，再用柯西不等式

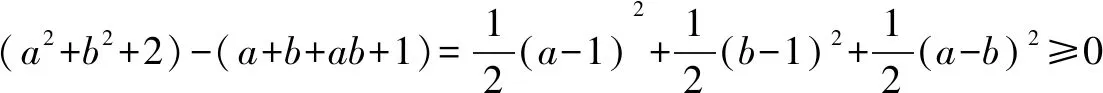
a2+b2+2≥(a+b)+(ab+1).

于是，由柯西不等式可得：

≥(1+1)2=4，

当且仅当a=1,b=1时取等号.

像上面的题，无法直接用柯西不等式，必须用其他不等式预处理下.又如：

例8 (数学通讯问题306)已知正数a,b,c满足abc=1，求证：

≥(1+1+1)2=9.

当且仅当a=b=c=1时取等号.

评析以后，当我们看到一题无法直接用柯西不等式解决时，不能放弃柯西不等式，要想到先运用均值不等式，配方等方法预处理后，再用柯西不等式试试.

4.先用柯西不等式处理，再用其他不等式证明题目

例9 (2018年陕西省联赛二试)设a,b,c,均为正实数，求证：

证明由柯西不等式可得：

故只需证：

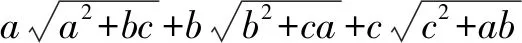
由均值不等式，得：

故只需证：

≥2(ab+bc+ca)①.

令a=x2,b=y2,c=z2,则由舒尔不等式及均值不等式得：

=x4+y4+z4+xyz(x+y+z)

≥x3(y+z)+y3(z+x)+z3(x+y)

≥2(x2y2+y2z2+z2x2)=2(ab+bc+ca),

即①式成立，故原不等式成立.

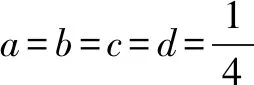
例11 (2018年广西预赛)设a1,a2,…,an为非负数，求证：

证明用数学归纳法来证明:

(1)当n=1时，结论显然成立.

(2)假设当n=k(k为正整数)时，结论对任意k个非负数成立.则n=k+1时，对任意k+1个非负数a1,a2,…,ak,ak+1，根据归纳假设有：

从而有：

下面证明：

由柯西不等式可得：

于是有：

故

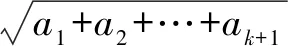
即①式成立，于是，n=k+1时，结论成立.

综合(1)(2)，对任意非负数a1,a2,…,an，结论都成立.

评析在解决一道难题时，也可用柯西不等式先处理下，再用其他的方法如数学归纳法去证明.这体现了考察柯西不等式与其他不等式知识的交汇十分频繁，我们必须要掌握好柯西不等式.

柯西不等式在解题中既有一定的独立性，又经常与其他知识进行交汇，所以通过柯西不等式能命制出很多精彩的试题，我们要想做出这些题目，必须要非常了解柯西不等式的运用及其延拓形式.以上是笔者对柯西不等式在解题中的四种运用的一些见解，不足之处，希望各位专家批评指正.