巧解圆中的范围问题

2020-07-09 06:04吴亭

吴亭

（江苏省木渎高级中学，215000）

解析几何就是在建立坐标系的基础上，利用“数”的办法来解决“形”的问题.其运算量大，过程繁琐，对思维要求也高，是高考的难点之一.如果我们能够充分挖掘图形的几何关系，结合严密的代数运算，就可相对巧妙地处理圆中的范围问题.

一、分析动静关系，巧用转化思想

例1 在平面直角坐标系xOy中，圆O：x2+y2=1，圆M：（x+a+3）2+（y-2a）2=1（a为实数）.若圆O与圆M上分别存在点P、Q，使得 ∠OQP=30°，则a的取值范围为________.

分析问题中的圆心M动中有定，它在定直线2x+y+6=0上运动，P，Q分别是定圆O与动圆M上的动点.可以考虑将等量关系“∠OQP=30°”转化为关于“线段OQ长”的不等关系，从而求出参数a的取值范围.

解过Q作QR与圆O切于点R，则∠OQR≥30°，得OQ≤2.又OM-1≤OQ≤OM+1，

评注在动态问题的分析中，将动点与定点、定直线综合考虑，巧妙地将动态问题向静态问题转化，可以有效避免盲目地寻找方程或不等式和进行相对繁琐的代数运算.

例2 已知圆C：x2+y2=4和直线l：x+y-3=0，若圆C上存在两点A，B，使得以AB为直径的圆与直线l有公共点P，则点P的横坐标范围是_______.

分析实际教学中，学生对“以AB为直径的圆与直线l有公共点P”的处理感到棘手，易被问题导向直线与圆的位置关系.而转化为∠APB=90°，问题则变得常规而亲切了.

解由以AB为直径的圆与直线l有公共点P，知∠APB=90°.过点P作PQ、PR与圆C切于Q、R，则 ∠QPR≥ ∠APB=90°，即∠OPR≥45°，故OP≤ 22.设点P的横坐标为x0，则，解得

评注定直线上的动点与圆上两个动点构成定角的问题是学生熟悉的，在变换表述方式后，我们需要通过对条件的挖掘，根据学生已有的经验作出判断，将未知问题向已知问题转化.

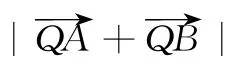
分析问题中的条件“直线l交圆于A，B两点”和目标“”均指向弦AB的中点，根据垂径定理发现弦AB中点的轨迹是以CP为直径的圆.

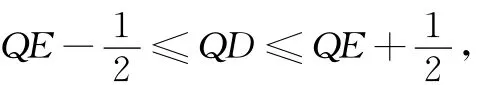
评注垂径定理和“隐圆”在圆中应用广泛，教学时要注重对学生“隐性”轨迹意识的培养，将两者结合起来考察，体现了分析问题时对常规思路的重视.当然，阿波罗尼斯圆在圆中的考察也很普遍.

例4 已知定点M（-1，2），动点N在单位圆x2+y2=1上运动，以OM，ON为邻边作平行四边形OMPN，则点P到直线2x+y+5=0距离的取值范围是_______.

分析从条件“OM，ON为邻边作平行四边形OMPN”出发，可以得到点P在以点M为圆心，1为半径的圆上.然而点P的轨迹不是整个圆，还需要去掉两个点.

评注在利用轨迹法巧妙发现“隐圆”时，需要检验轨迹的纯粹性.剔除“隐圆”上不合题意的点，培养学生思考问题的严谨性.另外，可以作如下变式：

变式1 将“以OM，ON为邻边作平行四边形OMPN”改为“”，则轨迹中不需要剔除直线OM与圆M的两个交点，（答案为：

变式2 将问题中的“直线2x+y+5=0”改为“直线3x+4y+15=0”，我们发现点P的轨迹“隐圆”依然要去除两点，而这两点到直线的距离却不被剔除.（答案为：［3，5］）

例5 已知圆C：x2+（y-1）2=r2（2≤r≤3），点A为圆C与x轴负半轴的交点，过点A作圆的弦AB，记线段AB的中点为M.若OA=OM，则直线AB的斜率的取值范围是_______.

分析在实际教学中，学生利用垂径定理可以发现OAMC四点共圆，之后的代数法选择正弦定理或者韦达定理计算量都较大.此时不妨分析几何图形特征，由点A为圆C与x轴负半轴的交点，联想到圆C与x轴正半轴的交点D与A关于原点O对称，得OA=OM=OD.又CM⊥AM，知M、C、D三点共线，则问题迎刃而解.

解设圆C与x轴正半轴的交点为D，则OA=OM=OD，易得 ∠AMD=900.又∠AMC=900，故M，C，D三点共线，所以kAB·kCD=-1.因为，所以

评注借助圆的几何特征，发现关系OA=OM=OD，并与平面几何中的结论“直角三角形斜边上的中线长等于斜边长的一半”建立联系，巧妙地将复杂计算变得十分简洁.

例6 已知圆O：x2+y2=4，两个定点A（2，2），B（m，1），P为圆O上任意一点，且PA

（1）求常数m的值；

（2）过点E（2，t）作直线l与圆C：x2+y2=m交于M、N两点，若M点恰好是线段NE的中点，求实数t的取值范围.

分析第（1）小题利用恒成立可得m=1；第（2）小题可以利用中点坐标公式将问题转化为两圆位置关系，也可以借助垂径定理，通过图形中的几何关系来解决.

评注由垂径定理构造直角三角形，巧妙利用勾股定理建立关系，最终转化为动点与定点之间的距离问题.

圆中的范围问题本质是以圆为背景的动态问题.通常从建立动点与圆心或弦中点的关系入手，充分利用圆的几何性质，挖掘隐性轨迹，辩证认识动静的关系，考虑将动态问题向静态问题转化.从而在定性分析的基础上，结合平面直角坐标系进行定量运算，数形结合，化繁为简.