探明究竟,大道至简——对2018年广州市一道中考题的研究

广东省广州市天河中学(510630) 叶小莹

广东省广州市教育研究院(510030) 陈镇民

1 试题呈现

(2018 年广州市中考第24 题) 已知抛物线y=x2+mx −2m −4(m ＞0).

(1)证明: 该抛物线与x轴总有两个不同的交点;

(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.

①试判断: 不论m取任何正数,⊙P是否经过y轴上某个定点? 若是,求出该定点的坐标;若不是,说明理由;

②若点C关于直线x=的对称点为点E, 点D(0,1),连接BE,BD,DE,ΔBDE的周长记为l,⊙P的半径记为r,求的值.

下面聚焦第(2)— ①问,研究过抛物线与坐标轴的交点的动圆是否过定点的问题,其它两问不作深入研究.

解如图1, 不论m取任何正数,⊙P经过y轴上定点(0,1).理由如下: 令y= 0, 得x2+mx −2m −4 =0, ∵m ＞0, ∴Δ =m2−4(−2m −4) = (m+4)2＞0, ∴x=∴x1==−m −2.∵m ＞0, ∴−m −2＜0.∴−m −2＜2.∵点A在点B的右侧,∴B(−m −2,0),A(2,0).∴AO=2,BO=m+2.

令x= 0, 得y=−2m −4, ∵m ＞0, ∴−2m −4＜0.∴C(0,−2m −4) 在y轴的负半轴.∴OC= 2m+4.∵A,B,C三点都在⊙P上, ∴⊙P也与y轴的正半轴有交点,设这个交点为K(0,k), 即KO=k.∵A,B,C,K四点都在⊙P上,∴∠AKO= ∠ABC.∵∠AOK= ∠COB= 90°,∴ΔAOK∽ΔCOB.∴k=1.∴K(0,1).∴不论m取任何正数,⊙P经过y轴上定点(0,1).

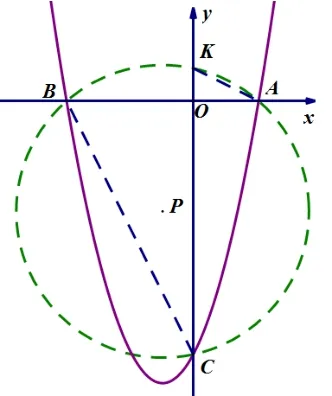
图1

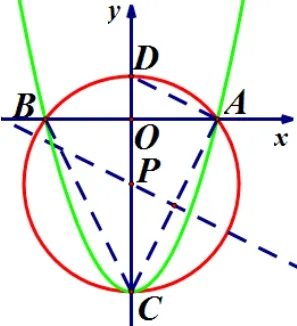
图2

2 问题探究

2.1 探究1已知抛物线y=x2+mx −2m −4.设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.试判断: 随着m的变化,⊙P是否经过y轴上某个定点? 若是,求出该定点的坐标;若不是,说明理由.

分析: 探究1 是在原试题的题干上去掉了“m ＞0”的条件,需要对参数m的取值范围进行讨论.

解(1)当m ＞0 时,抛物线的对称轴在y轴的左侧.由原试题知,⊙P经过y轴上定点(0,1).

(2) 当m= 0 时, 抛物线为y=x2−4, 则A(2,0),B(−2,0),C(0,−4),抛物线的对称轴是y轴.∴AO=BO=2,CO=4.设定点为D,坐标为(0,d).

下面提供两种思考方法.

法1(几何法): 由抛物线和圆的对称性,可得圆心点P在y轴上,如图2,∵A,B,C三点都在⊙P上,⊙P经过点D,∴A,B,C,D四点共圆.∴∠ADO= ∠CBO,∠AOD= ∠COB.∴ΔADO∽ΔCBO.∴∴DO=1.即D(0,1).

法2(坐标 法) : 设P(0,p), ∵A,B,C,D四点 共 圆,∴AP=DP=解得d= 1, 即D(0,1).∴当m= 0 时,⊙P经过y轴上定点(0,1).

(3)当m ＜0 时,抛物线的对称轴在y轴的右侧.

①当m=−2 时, 抛物线为y=x2−2x, 如图3, 则A(2,0),B(0,0),C(0,0).此时有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).

图3

图4

②当m=−4 时,抛物线为y=x2−4x+4,如图4,则A(2,0),B(2,0),C(0,4).此时有无数个圆经过A,B,C三点.这些圆恒过定点(0,4).

③当−2＜m ＜0 时,如图5,令y= 0,解得:x1= 2,x2=−m −2.∵−2＜m ＜0,∴−2＜−m −2＜0.∵点A在点B的右侧, ∴A(2,0),B(−m −2,0),C(0,−2m −4).∴B点在x轴负半轴,C点在y轴负半轴.∴OA= 2,OB=m+2,OC= 2(m+2).易证ΔAOD∽ΔCOB.∴OD=1,即D(0,1).

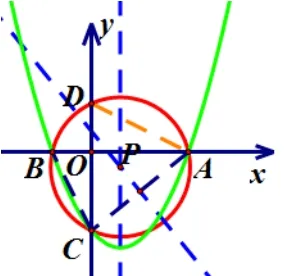
图5

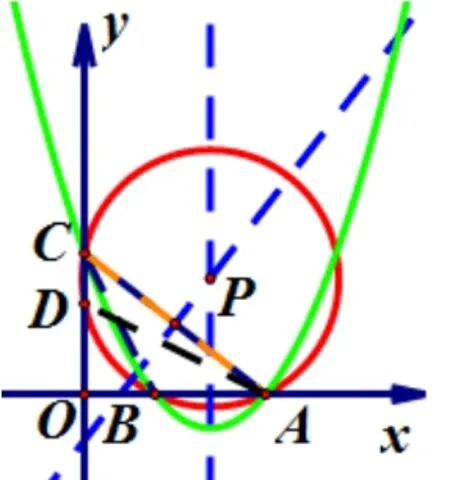
图6

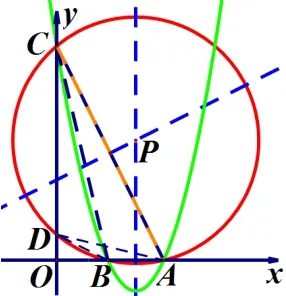
图7

④当−4＜ m ＜ −2 时, 如图6, 令y= 0, 解得:x1= 2,x2=−m −2.∵−4＜ m ＜ −2, ∴0＜−m −2＜2, 0＜−2m −4＜2.∵点A在点B的右侧,∴A(2,0),B(−m −2,0),C(0,−2m −4).∴B点在x轴正半轴,C点在y轴正半轴.∴OA= 2,OB=−(m+2),OC=−2(m+2).∵∠AOD= ∠COB,∠OAD= ∠OCB,∴ΔAOD∽ΔCOB.∴OD=1,即D(0,1).

⑤当m ＜−4 时,如图7,令y=0,解得:x1=2,x2=−m−2.∵m ＜−4,∴−m−2＞2,−2m−4＞4.∵点A在点B的右侧,∴A(−m −2,0),B(2,0),C(0,−2m −4).∴B点在x轴正半轴,C点在y轴正半轴.∴OA=−(m+2),OB=2,OC=−2(m+2).∵∠AOD= ∠COB,∠OAD= ∠OCB,∴ΔAOD∽ΔCOB.∴OD=1,即D(0,1).

综上所述,当m=−2 时,⊙P恒过原点;当m=−4 时,⊙P恒过(0,4);当m/=−2 且m/=−4 时,⊙P恒过D(0,1).

2.2 探究2抛物线解析式改为y=x2+bx+c.设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.问⊙P是否经过y轴上某个定点? 若是,求定点的坐标;若不是,说明理由.

分析: 探究2 是把抛物线解析式从一个参数“m”拓展到两个参数“b”和“c”,进一步研究过抛物线与坐标轴的交点的圆是否能过定点的问题.

解∵抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,∴Δ=(−b)2−4c=b2−4c ＞0,C(0,c).设A(x1,0),B(x2,0),x1＞ x2, ∴x1· x2=c,x1+x2=−b.∵A,B,C三点都在⊙P上,

(1) 当c ＞0 时, 点C在y轴正半轴, 即OC=c.∴x1·x2＞0,即x1,x2同号.

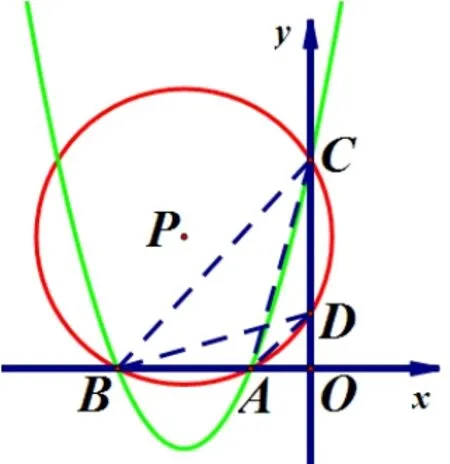
图8

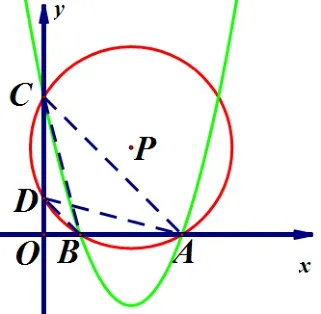
图9

①当x1＜0,x2＜0 时,如图8,则⊙P还经过y轴上一点D,即A,B,C,D四点共圆.∴A,B两点都在x轴负半轴, ∴AO=−x1,BO=−x2, 点D在y轴正半轴.∵A,B,C,D四点共圆, ∴∠DBO= ∠ACO.∵∠DOB= ∠AOC,∴ΔDOB∽ ΔAOC.∴DO==1,即D(0,1).

②当x1＞0,x2＞0 时, 如图9, 则⊙P还经过y轴上一点D, ∴A,B两点都在x轴正半轴.∴AO=x1,BO=x2, 点D在y轴正半轴.∵A,B,C,D四点共圆, ∴∠DAO= ∠BCO.∵∠DOA= ∠BOC, ∴ΔDOA∽ΔBOC.∴即D(0,1).∴当c ＞0 时,⊙P恒过定点(0,1).

(2)当c=0 时,∴x1·x2=0,即x1=0 或x2=0.

①当x1= 0 时,如图10.∴A,C,O三点重合.∴有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).

②当x2= 0 时,如图11.∴B,C,O三点重合.∴有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).∴当c=0时,⊙P恒过定点(0,0).

图10

图11

(3) 当c ＜0 时, 点C在y轴负半轴, 即OC=−c.∴x1·x2＜0,即x1,x2异号.∵x1＞x2,∴x1＞0,x2＜0.

①当抛物线的对称轴在y轴左侧时, 如图12, 则⊙P还经过y轴上一点D,且点D在y轴正半轴.∴A点在x轴正半轴,B点在x轴负半轴.∴AO=x1,BO=−x2,∵A,B,C,D四点共圆, ∴∠DBO= ∠ACO.∵∠DOB= ∠AOC,∴ΔDOB∽ ΔAOC.即D(0,1).

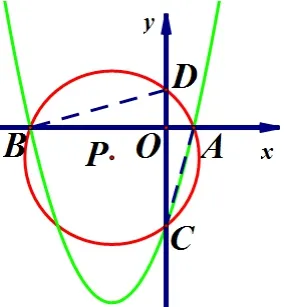
图12

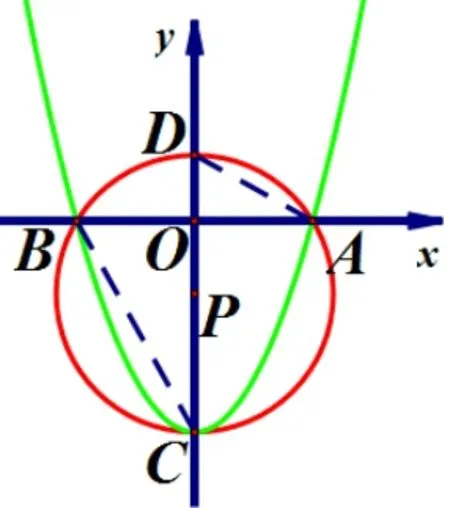
图13

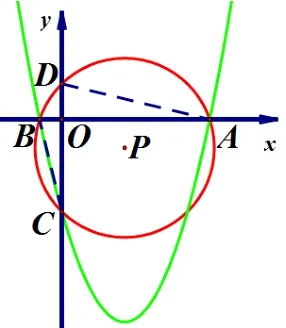
图14

②当抛物线的对称轴在y轴上时,如图13,则⊙P还经过y轴上一点D, 且点D在y轴正半轴.∴A点在x轴正半轴,B点在x轴负半轴.∴AO=x1,BO=−x2,点D在y轴正半轴.∵A,B,C,D四点共圆,∴∠DAO= ∠BCO.∵∠DOA= ∠BOC,∴ΔDOA∽ΔBOC.即=1,即D(0,1).

③当抛物线的对称轴在y轴右侧,如图14,则⊙P还经过y轴上一点D,且点D在y轴正半轴.∴A点在x轴正半轴,B点在x轴负半轴.∴AO=x1,BO=−x2.∵A,B,C,D四点共圆, ∴∠DAO= ∠BCO.∵∠DOA= ∠BOC,∴ΔDOA∽ ΔBOC.= 1, 即D(0,1).∴当c ＜0时,⊙P恒过定点(0,1).

综上所述,在b2−4c ＞0 的前提下,当c=0 时,⊙P恒过定点(0,0);当c/=0 时,⊙P恒过定点(0,1).

2.3 探究3抛物线解析式改为y=ax2+bx+c(a/=0).设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.问⊙P是否经过y轴上某个定点? 若是,求定点的坐标;若不是,说明理由.

分析: 本题进一步增加参数个数,把抛物线解析式变为一般式,研究结论是否具有一般性.

解∵抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,∴Δ=(−b)2−4ac=b2−4ac ＞0,C(0,c).设A(x1,0),B(x2,0),x1＞x2, ∴x1· x2=∵A,B,C三点都在⊙P上,类比探究1 和探究2,可知⊙P还经过点D,且点D在y轴上.即A,B,C,D四点共圆.

(1)当a ＞0,c ＞0 时,抛物线开口向上,点C在y轴的正半轴,即OC=c.

①当x1＜0,x2＜0 时, 如图15.则A,B两点都在x轴负半轴上.∴AO=−x1,BO=−x2, 点D在y轴正半轴.∵A,B,C,D四点共圆, ∴∠DBO= ∠ACO.

∵∠DOB= ∠AOC,∴ΔDOB∽ΔAOC.∴即即

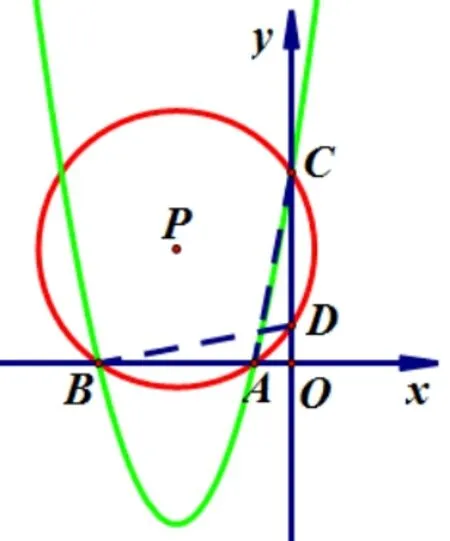
图15

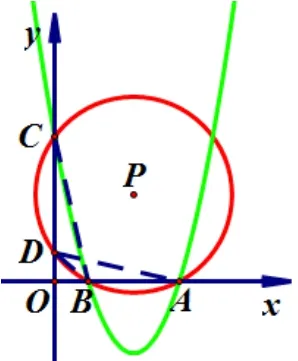
图16

②当x1＞0,x2＞0 时, 如图16.则A,B两点都在x轴正半轴上.∴AO=x1,BO=x2, 点D在y轴正半轴.∵A,B,C,D四点共圆, ∴∠DAO= ∠BCO.∵∠DOA= ∠BOC,∴ΔDOA∽ΔBOC.即即

(2)当a ＜0,c ＜0 时,抛物线开口向下,点C在y轴的负半轴,即OC=−c.

①当x1＜0,x2＜0 时, 如图17.则A,B两点都在x轴负半轴上.∴AO=−x1,BO=−x2, 点D在y轴负半轴.∵A,B,C,D四点共圆, ∴∠DBO= ∠ACO.∵∠DOB= ∠AOC,∴ΔDOB∽ΔAOC.即

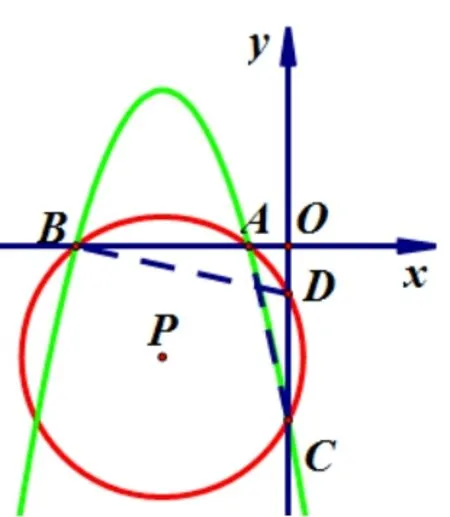
图17

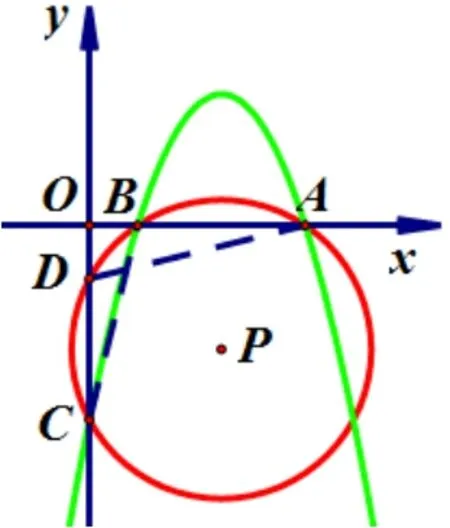
图18

②当x1＞0,x2＞0 时, 如图18.则A,B两点都在x轴正半轴.∴AO=x1,BO=x2, 点D在y轴负半轴.∵A,B,C,D四点共圆, ∴∠DAO= ∠BCO.

∵∠DOA= ∠BOC,∴ΔDOA∽ΔBOC.即即∴当时,⊙P恒过定点

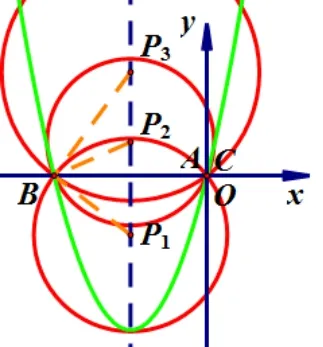
图19

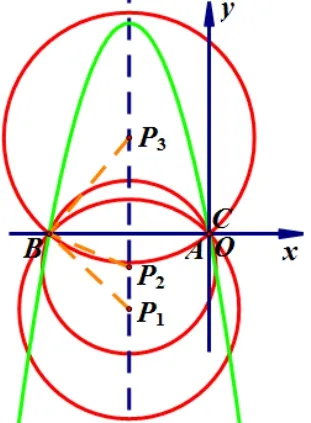
图20

(1)当x1=0 时,即A(0,0).故A,C,O三点重合.

①当a ＞0 时,抛物线开口向上,如图19.则有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).

②当a ＜0 时,抛物线开口向下,如图20.则有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).

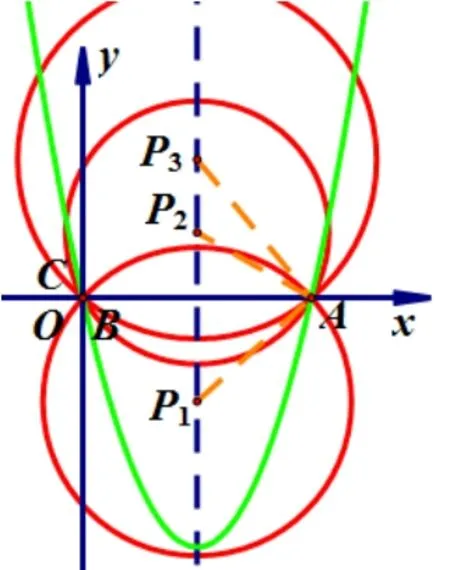
图21

图22

(2)当x2=0 时,即B(0,0).故B,C,O三点重合.

①当a ＞0 时,抛物线开口向上,如图21.则有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).

②当a ＜0 时,抛物线开口向下,如图22.则有无数个圆经过A,B,C三点,这些圆恒过定点(0,0).∴当=0 时,⊙P恒过定点(0,0).

(1) 当a ＞0,c ＜0 时, 抛物线开口向上, 点C在y轴的负半轴, 即OC=−c.当x1＞0,x2＜0 时,如图23.则点A在x轴正半轴, 点B在x轴负半轴.∴AO=x1,BO=−x2, 点D在y轴正半轴.∵A,B,C,D四点共圆, ∴∠DBO= ∠ACO.∵∠DOB= ∠AOC,∴ΔDOB∽ ΔAOC.

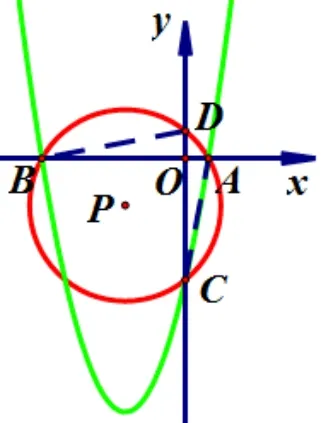
图23

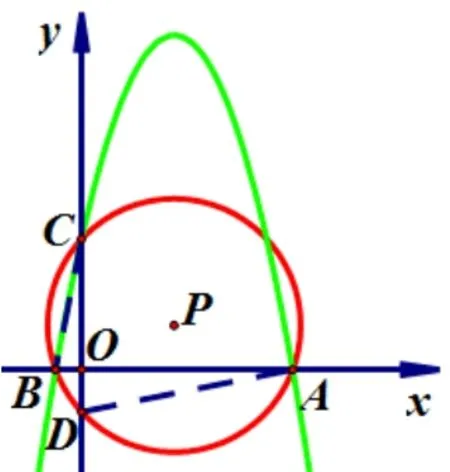
图24

(2)当a ＜0,c ＞0 时,抛物线开口向下,点C在y轴的正半轴,即OC=c.当x1＞0,x2＜0 时,如图24.则点A在x轴正半轴,点B在x轴负半轴.∴AO=x1,BO=−x2,点D在y轴负半轴.∵A,B,C,D四点共圆,∴∠DAO= ∠BCO.∵∠DOA= ∠BOC,∴ΔDOA∽ΔBOC.∴,即即时,⊙P恒过定点

3 探究启示

美国数学家哈尔莫斯曾说过: 问题是数学的心脏.如何通过数学问题的教学有效提升学生的解题能力,是数学的一项重要任务.在我们日常教学中,既要讲清某个数学问题是怎样解答的,又要把握问题的本质属性,探明问题究竟,同时要进行适当的拓展延伸,掌握问题的一般规律,使问题的解决达到“至简至易”的境界.

著名学者南怀瑾先生在他所著述的《易经杂说》一书中说道: 真懂了《易经》,一点都不神秘,最高的道理,也是最平凡的道理.从以上探究过程来看,试题、探究1 和探究2,其实是探究3 中当a=1 时的特例,弄明白了问题的来龙去脉,这个问题也就是很平凡的问题了.