“十字”模型及其应用

江苏省南京市板桥中学(210039) 纪明亮

几何是初中数学的重点和难点,有的时候为一道几何题苦思冥想很久还是无法解答,有时为一道几何题能巧妙的作出一种辅助线使问题解决而感到欣喜若狂,那么几何题究竟为何这样难以驾驭? 其实几何题看似变幻莫测,但每道题都是有章可循的,可从中抽象出基本模型,抓住基本模型就可以抓住几何题的本质,方能以不变应万变,“十字”模型就是一类重要的几何模型,但此种几何模型的研究并不多,本文对“十字”模型做了一些思考和研究,并将思考和研究的结果与大家分享.

1 模型分析

(1)正方形中“十字”模型1

如图1, 在正方形ABCD中,E、F、G、H分别为AB、CD、BC、AD上的点, 若EF⊥GH于点O, 结论:EF=GH.

证明: 如图1, 过点E、G分别作EN⊥CD、GM⊥AD于N、M, 则∠ENF= ∠GMH= 90°,EN⊥GM于点P,EN=GM则∠EPG= 90°.由EF⊥GH于点O, 则∠EOG= 90°.由∠EPG+∠NEF= ∠MGH+∠EOG,则∠NEF= ∠MGH, 故ΔEFN∽= ΔGHM(ASA), 则EF=GH.

图1

图2

(2)正方形中“十字”模型2

如图2, 在正方形ABCD中,E、F、G、H分别为AB、CD、AB、BC上的点, 若EF⊥GH于点P, 结论:

证明: 过点F作FQ⊥AB于Q, 则∠EQF= 90°, 则∠EQF= ∠B, 由EF⊥GH于点P, 则∠GPE= 90°, 则∠GPE= ∠B, ∠QEF+ ∠EGP= ∠BHG+ ∠EGP则∠QEF= ∠BHG, 故ΔQEF∽ΔBHG, 则即

(3)矩形中“十字”模型

如图3, 在长方形ABCD中,E、F、G、H分别为AB、CD、BC、AD上的点, 若EF⊥GH于点O, 结论:

证明: 如图3, 过点E、G分别作EN⊥CD、GM⊥AD于N、M,则∠ENF= ∠GMH= 90°,EN⊥GM于点P,则∠EPG= 90°, 由EF⊥GH于点O, 则∠EOG= 90°,由∠EPG+ ∠NEF= ∠MGH+ ∠EOG, 则∠NEF=∠MGH,故ΔEFN∽ΔGHM,则

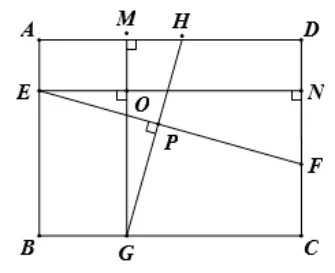
图3

图4

“十字”模型是以线段“垂直”为基础,在正方形、矩形里构建直角三角形,再借助“垂直”关系证明所构建的直角三角形全等或相似得到相应的边之间的数量关系,这是对“垂直”这一条件作用的升华,使其在解题中发挥更大作用.那么什么题目符合“十字”模型?“十字”模型在解题中的关键作用是什么? 下面通过几道题目回答这两个问题.

2 模型应用

题1如图4, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC= 4, 点D是BC中点,CE⊥AD于点F, 交AB于点E,求CE的长.

分析: 因为CE⊥AD于点F,且ΔABC是等腰直角三角形,这是正方形中的“十字”模型1,可根据此模型作辅助线构建图形解题.

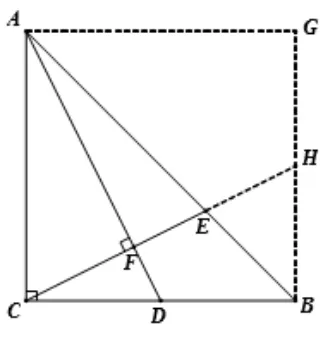
图5

解如图5, 以CA、CB为邻边构造正方形ACBG,延长CE交BG于点H.由四边形ACBG是正方形,则∠ACD= ∠CBH= 90°,AC//BG,由BC=4,点D是BC中点, 则CD= 2.在RtΔACD中根据勾股定理, 可得AD=由CE⊥AD于点F,则∠AFD= 90°,则∠CAD+∠ACF=90°, 由∠ACF+ ∠BCH= 90°, 则∠CAD= ∠BCH,再 由AC=CB, 故RtΔACD∽= RtΔCBH(ASA), 则CH=AD=BH=CD= 2(“十字”模型) .由AC//BG,故ΔACE∽ΔBHE,则则即CE=

点评: 几何计算一般采用勾股定理(建方程)、三角形相似、三角函数、等积法等方法, 而题中CE不在直角三角形中,则不能直接用勾股定理和三角函数求解,其所在三角形在原图中也很难找到与之相似的三角形,等积法也很难行得通,这就需要作辅助线,那么辅助线如何作? 这里“CE⊥AD于点F,且ΔABC是等腰直角三角形”就是突破口,这是正方形中“十字”模型1 的典型特征,由此引领本题如何作辅助线构建图形解题.

变式1如图6, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC= 4, 点D、M分别是BC、AC上的点, 且满足BD=CM= 1,CE⊥DM于点F,交AB于点E,求CE的长.

分析: 因为“CE⊥DM于点F,且ΔABC是等腰直角三角形,点D、M分别是BC、AC上的点”,这是正方形中的“十字”模型2,可根据此模型构建图形解题.

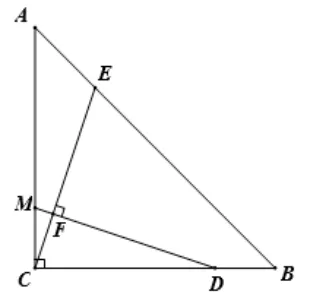
图6

图7

解如图7, 以CA、CB为邻边构造正方形ACBG,并延长CE交BG于点H.由四边形ACBG是正方形, 则∠ACB= ∠CAG= 90°,BC//AG, 由BC= 4,BD= 1, 则CD= 3, 在RtΔCDM中 根 据 勾 股定 理得DM=由CE⊥DM于点F, 则∠CFD= 90°, 则∠CDF+ ∠FCD= 90°, 并由∠FCD+ ∠ACH= 90°, 可得∠ACH= ∠CDF, 故ΔACH∽ΔCDM, 则可 得CH=由BC//AG,故ΔBEC∽ ΔAEH, 则= 3, 则

点评: 本题情况和题1 类似,CE的长度很难求出,需要作辅助线,构建图形.同样这里“CE⊥AD于点F,且ΔABC是等腰直角三角形”,显然这是正方形中“十字”模型,通过构造出正方形,发现这是正方形中的“十字”模型2,根据这个模型,将所求线段化归到三角形中利用相似关系求出.

变式2如图6, 在等腰RtΔABC中, ∠ACB= 90°,AC=BC=4,点D在BC上的点(不与点B、C重合),点M在AC边上,满足BD=CM,CE⊥DM于点F,交AB于点E,求的值.

分析: 因为CE⊥DM于点F,且ΔABC是等腰直角三角形,这是正方形中的“十字”模型2,可根据此模型构图解题.

解如图7, 以CA、CB为邻边构造正方形ACBG,延长CE交BG于点H.由四边形ACBG是正方形, 则∠ACB= ∠CAG= 90°,且BC//AG.设BD=CM=x,由BC= 4,则CD= 4−x,在RtΔCDM中根据勾股定理得DM=由CE⊥DM于点F,则∠CFD= 90°,则∠CDF+∠FCD= 90°,再由∠FCD+∠ACH=90°,则∠ACH=∠CDF,故ΔACH∽ΔCDM, 则即则CH=由BC//AG, 故ΔBEC∽ ΔAEH, 则即, 则CE=

点评: 本题是变式1 当中问题的一般化,D、M都是动点,但任满足BD=CM,从变式1 可以发现CE=DM,那么本题中关键就是求出CE、DM的数量关系,如果仅从原有图形思考很难有所进展,显然要作辅助线构图,这与变式1的模型相同,也是正方形中的“十字”模型2,可根据此模型构建图形,由于D、M都是动点,可设BD=CM=x,便于求出CE、DM的数量关系,解决问题.

变式3如图8,在ΔABC中,AB=AC,∠ABC=60°,点D在AB边上(不与点A、B重合),点E在AC边上,满足CE=AD,过点A作AH⊥DE于点F,交BC于点H,求值.

分析: 因为“点D在AB边上(不与点A、B重合),点E在AC边上AH⊥DE于点F,且ΔABC是等边三角形,”,这是矩形中“十字”模型,可根据此模型将问题划归到矩形中借助矩形中“十字”模型来解决问题.

图8

图9

解如图9, 以BC为边, 点A对边上一点构造矩形BCSR, 延长DE交BE、CR于M、P, 过点M, 作MN⊥CS于点N, 在CS上取点Q, 使EP=EQ, 过点A作AG⊥BC于点G.由于AG⊥BC于点G, 则AG⊥MN, 则∠OMN= ∠OAF, 由于MN⊥CS于点N,则∠MNP= 90°, 则∠MNP= ∠AGH, 则ΔMNP∽ΔAGH, 则由AG//CS, 则∠AOD= ∠EPQ.由EP=EQ,则∠EPQ= ∠EQP,则∠AOD= ∠EQP.由∠DAO= ∠ECQ= 30°,AD=CE,故ΔDAO∽= ΔECQ(AAS),则OD=EQ,则OD=EP.由OM=OP,则OD+MD=OE+EP,即MD=OE,则MD+EP=OD+OE, 则DE=

点评: 本题和变式2 类似,也是动点问题中求边的比值,直接求非常困难, 因此要依托于图形, 而点D在AB边上(不与点A、B重合),点E在AC边上AH⊥DE于点F,且ΔABC是等边三角形,这是矩形中“十字”模型,则根据此模型构造出矩形和直角三角形,再根据图形关系求出值.

3 结语

在解题中模型的作用实际上是解题思路的引领,每一种模型都可以推导出确定的结果,借助模型能更好的发现题目中的规律, 能透过现象看本质.在几何问题中有的条件(图形)给的非常隐晦,很难明白其用意,不知如何转化,那么问题就难以解决,像以上四道题,每道题都给了“垂直”,而“垂直”是“十字”模型的必要条件,这样可以试用“十字”模型构建图形,通过“十字”模型引领辅助线作法,巧妙构图,化难为易,将四道题都解决了.