有关三角形的内心与外心基本图形探究

湖北省武汉市鲁巷中学(430074) 熊 燕

初中数学中几何知识涉及面广、知识点多,几何图形纷繁复杂、千变万化,一直以来都是初中生学习的重点和难点.然而复杂的几何图形往往却是由一些简单的基本图形组合而成.初中数学教材中有不少内涵丰富、具有很强探究性的基本图形,如果能进一步有效挖掘,不但能巩固基础知识,增强学生变式能力,提高数学素养,还能培养学生的抽象思维、逻辑思维、形象思维、发散思维和创新思维.因此,笔者在日常教学中有意识地对一些基本的几何图形模型进行提炼和探究,并对这些基本的图形模型和基本结论的应用进行专题训练,以提高学生解决几何综合题的能力.

1 经典习题展示

练习1.(2013 年武汉市元月调考第10 题) 如图1, 点I和O分别是ΔABC的内心和外心, 则∠AIB和∠AOB的关系为( )

图1

A.∠AIB=∠AOB

B.∠AIB /=∠AOB

C.2∠AIB −=180°

D.2∠AOB −=180°

简解点O是ΔABC的外心, 所以∠C=又因点I是ΔABC的内心, 所以∠IAB=进而得到结论.

评析遇到三角形的外心,联想到圆心角与圆周角的两倍关系,遇到三角形的内心,联想到内心的定义,即三条角平分线的交点,进而灵活运用相关性质解决数学实际问题.本题主要考查圆周角定理和三角形内心和外心的相关性质,以及三角形内角和定理,解决初中数学中的计算问题.

练习2.(人教版九年级上册教材习题24.2 第14 题)如图2,在RtΔABC中,∠C= 90°,AB、BC、CA的长分别为c、a、b,求ΔABC的内切圆半径r.

简解一如图2, 过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F, 连接OA,OB,OC.因为圆O是三角形的内切圆, 所以OD=OE=OF=r, 又因为SΔABC=SΔAOB+SΔBOC+SΔAOC=在RtΔABC中,SΔABC=所以进而得到结论

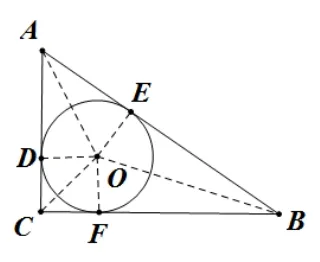
图2

简解二如图2, 过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F, 则∠ODC=∠OFC= ∠C= 90°, 所 以 四边形ODCF是矩形, 又因为OD=OF, 所以四边形ODCF是正方形, 由切线长定理可知,AD=AE,CD=CF,BF=BE, 所以BC+AC −AB= 2CD= 2OD, 即a+b −c= 2r,进而得到结论r=

补充如图3 求RtΔABC的外接圆半径R.

简解取线段AB的中点G,连接CG, 在RtΔABC中,AG=BG=CG=A、B、C三点在以点G为圆心的圆上,所以圆G是ΔABC的外接圆,其半径R=

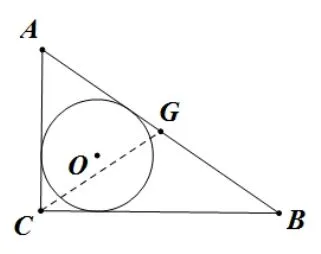
图3

评析遇到直角三角形的内心问题,联想到三角形面积公式和切线长定理,善于运用割补法计算三角形的面积,遇到直角三角形的外心问题,联想到“直角三角形斜边上的中线等于斜边长的一半”和“三点共圆”等初中数学几何性质,解决数学问题.本题通过两种不同的解法, 得到直角三角形内切圆半径r的两个数学表达式, 其本质是一样的.(注: 要证r=成立, 只需证(a+b+c)·(a+b −c) = 2ab成立, 即证a2+b2=c2成立,以上结论显然成立)本题是对教材上的习题的再创造,充分体现新课程标准中数学试题来源于教材又高于教材.

练习3.(人教版九年级上册教材复习题24 第13 题) 如图4, 点E是ΔABC的内心,AE的延长线和ΔABC的外接圆相交于点D.求证:DE=DB.

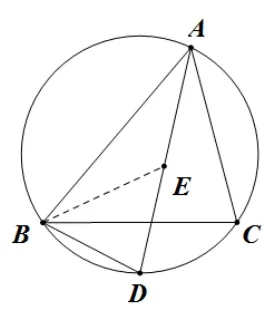
图4

简解连接BE, 因为点E是ΔABC的内心, 所以∠DAC= ∠DAB, ∠ABE= ∠CBE, 又因为弧CD=弧CD, 所以∠DAC= ∠DBC, 即∠DAB= ∠DBC, 又∠DBE= ∠DBC+∠CBE, ∠DEB= ∠DAB+∠ABE,所以∠DBE=∠DEB,进而得到结论DE=DB.

评析初中数学几何中遇到三角形的内心,联想到内心的定义,即三条角平分线的交点,进而灵活运用相关性质解决数学实际问题.本题根据内心定义和圆周角的相关性质,解决初中数学几何中的证明问题.

2 基本图形提炼

基本图形一:如图5,ΔABC中,∠A=α,点I是ΔABC的内心,则∠BIC=90°+如图6,ΔABC中,∠A=α,点O是ΔABC的外心,则∠BOC=2α.

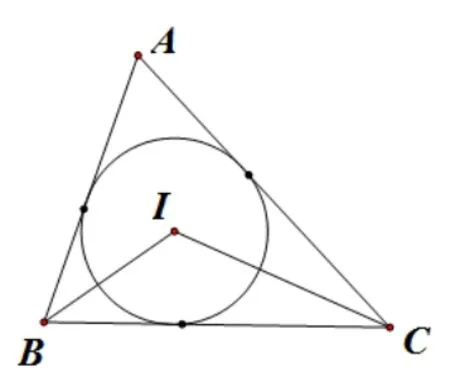
图5

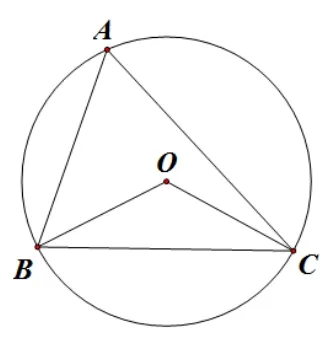
图6

基本图形二: 如图7, 在RtΔABC中,∠C=90°,⊙O为ΔABC的内切圆, 切点分别为D、E、F,若边BC、CA、AB的长分别为a、b、c, 则ΔABC的内切圆半径r=外接圆半径

图7

推广: 如图8, 在ΔABC中, 边BC、CA、AB的长分别为a、b、c, 先用割补法或双勾股法求出ΔABC的面积S,再计算ΔABC的内切圆半径

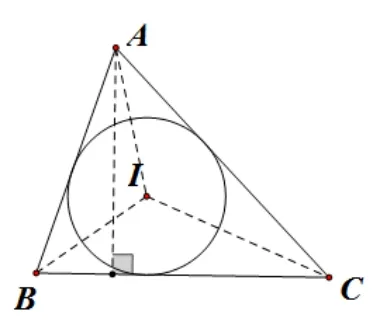
图8

基本图形三: 如图9, 点E是ΔABC的内心,AE的延长线和ΔABC的外接圆相交于点D, 则DE=DB=DC.(B、E、C三点在以D为圆心,DB长为半径的⊙D上)

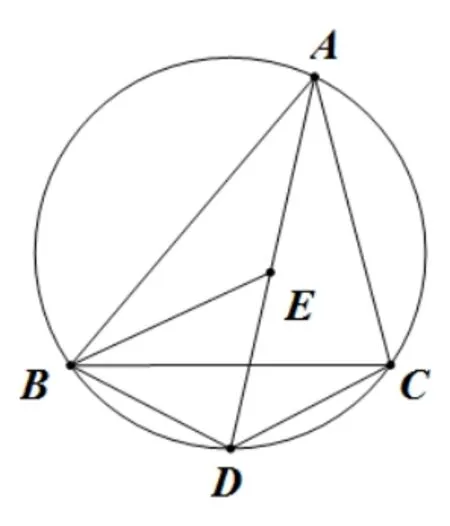
图9

3 基本图形应用

例1(人教版九年级上册教材24.2.2 练习第2 题)ΔABC的内切圆半径为r,ΔABC的周长为l,求ΔABC的面积.(提示: 设ΔABC的内心为O,连接OA,OB,OC.)

图10

图11

分析问题中要求解ΔABC的面积,根据上述基本图形二,很自然地联想到连接OA,OB,OC,将大三角形分割为三个小三角形,因此,这里采用割补法求面积.

解析如图11, 设ΔABC的内心为O, 连接OA,OB,OC,则OA=OB=OC=r,SΔABC=SΔAOB+SΔBOC+

评析本题属于教材中的练习题,主要考查三角形的周长、面积和内切圆半径之间的数量关系,运用基本图形二的推广,可以快速解决.

例2(2019 年武汉市中考第9 题)如图12,AB是⊙O的直径,M、N是弧AB(异于A、B) 上两点,C是弧MN上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时, 则C、E两点的运动路径长的比是( )

图12

分析如图13, 连接EB, 根据上述基本图形三, 易知点E在以D为圆心DA长为半径的圆上, 其运动轨迹是弧GF, 点C的运动轨迹是弧MN, 由题意∠MON= 2∠GDF, 再利用弧长公式计算即可解决问题.

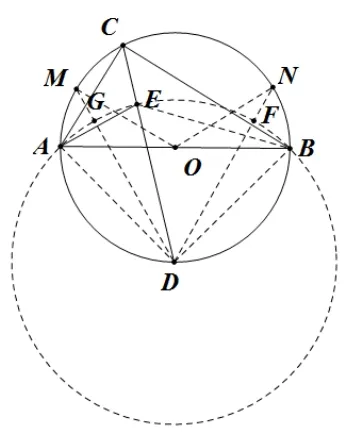
图13

解析如图13,连接EB、AD、BD、OM、ON、DM、DN,DM、DN分别与⊙D交于点G、F,设OA=r,则因为AB是直径,所以∠ACB= 90°,因为CE、AE分别是∠ACB、∠BAC的角平分线,所以E是ΔABC的内心,根据上述基本图形一,易知∠AEB= 135°.因为∠ACD= ∠BCD,所以弧AD=弧BD, 即AD=BD, 因为AB是直径, 所以∠ADB= 90°, 所以AD=BD=根据上述基本图形三, 易知点E在以D为圆心DA长为半径的圆上, 其运动轨迹是弧GF, 点C的运动轨迹是弧MN, 由题意可知∠MON= 2∠GDF, 设∠GDF=α, ∠MON= 2α, 故弧MN长=弧GF长=所以弧MN长/弧GF长=

评析本题考查弧长公式,圆周角定理,三角形内心的有关性质,解题的关键是理解题意,正确寻找到点的运动轨迹,属于中考选择题中的压轴题.

例3(2012 年武汉市元月调考改编)如图14,BC是⊙O的直径,半径为R,A为半圆上一点,I为ΔABC的内心,延长AI交BC于D点, 交⊙O于点E, 作IF ⊥BC, 连接AO,BI.下列结论: ①∠BAE=45°; ②4∠AIB−∠BOA=360°; ③BC=为定值,其中正确的结论有_______.

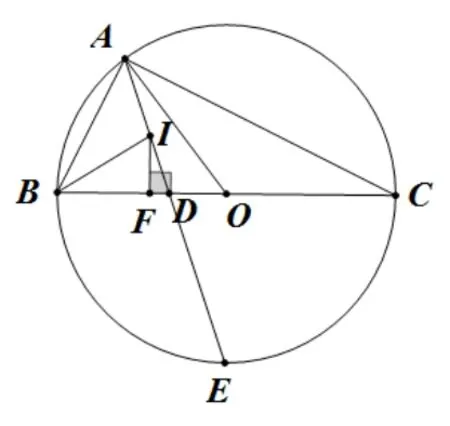
图14

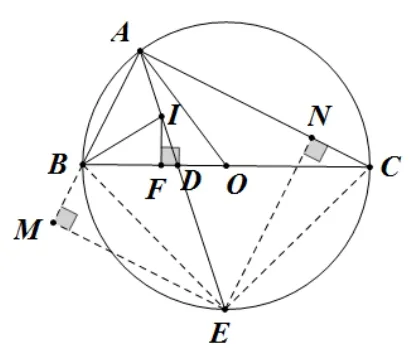
图15

分析①利用三角形内心的定义解答即可; ②根据上述基本图形一和圆周角定理可得结论; ③根据上述基本图形三和等腰直角三角形性质可得正确性; ④过E点作角两边的垂线, 可以由三角形全等及等腰直角三角形性质, 得到AB+AC=可得④正确; ⑤根据上述基本图形二得到直角三角形内切圆半径公式,再结合④的结论,可证得⑤正确.

解析①因为BC是⊙O的直径, 所以∠BAC=90°, 又因为I为ΔABC的内心, 所以AE平分∠BAC,即∠BAE= 45°, 正确; ②根据上述基本图形一, 因为I为ΔABC的内心, 所以∠BIA= 90°+即4∠BIA= 360°+ 2∠C, 又因为∠BOA= 2∠C, 所 以4∠AIB−∠BOA=360°,正确; ③如图15,连接BE、EC,根据上述基本图形三,易知BE=EI=EC,因为BC是⊙O的直径, 所以∠BEC= 90°, 所以BC=正确; ④过点E作EM⊥AB于M,EN⊥AC于N,则四边形ENAM是矩形,∠ENC= 90°,∠EMB= 90°,由①可知, ∠BAE= 45°, 所以AM=EM, 所以四边形ENAM是正方形, 所以AM+AN=√EM=EN, 又因为∠CEN+ ∠NEB= 90°,∠MEB+ ∠NEB= 90°,所以∠CEN= ∠MEB, 所以ΔCEN∽= ΔBEM, 所以CN=BM, 所以AB+AC=正确; ⑤根据上述基本图形二, 易知IF为RtΔABC内切圆半径,IF=即AB+AC=BC+2IF=2R+2IF,即IF+R=由④可知,AB+AC=所以,正确.

评析本题是中考数学填空题中多结论试题,综合考查了与圆有关的知识,直角三角形内切圆的半径公式,利用直角三角形的内切圆的圆心是内角平分线的交点,并作出辅助线构造全等三角形是解决本题的难点.灵活应用上述三个基本图形的有关结论,对解决本题提供了帮助.

4 结语

著名数学家波利亚曾经说过:“解题的成功,要靠正确的转化.”在教学中,特别是在复杂的几何图形分析的过程中,帮助学生从典型题目中总结提炼出基本图形,学会从复杂的几何图形中拆分出基本图形,或者需要添加辅助线来解决问题时,构造基本图形能快速地解决问题,同时培养学生的识图能力和逻辑推理能力.